目录

1、509. 斐波那契数 

2、1137. 第 N 个泰波那契数

3、118. 杨辉三角

4、119. 杨辉三角 II

5、70. 爬楼梯

6、剑指 Offer 62. 圆圈中最后剩下的数字

7、剑指 Offer II 092. 翻转字符

8、剑指 Offer II 098. 路径的数目

---

1、509. 斐波那契数 

斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1

给定 n ，请计算 F(n) 。

示例：

输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1

思路：

1. 递归
2. 迭代

int fib(int n){
    // if(n == 1 || n == 0)
    //     return n;
    // return fib(n - 1) + fib(n - 2);
 
    if(n == 1 || n == 0)
        return n;
    int a = 0;
    int b = 1;
    int c = 0;
    for(int i = 2; i <= n; i++){
        c = a + b;
        a = b;
        b = c;
    }
    return c;
}

2、1137. 第 N 个泰波那契数

泰波那契序列 Tn 定义如下： T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2给你整数 n，请返回第 n 个泰波那契数 Tn 的值。

示例：

输入：n = 4
输出：4
解释：
T_3 = 0 + 1 + 1 = 2
T_4 = 1 + 1 + 2 = 4

思路：迭代

int tribonacci(int n){
    if(n == 0 || n == 1 || n == 2)
        return (n == 0 ? n : 1);
    int a = 0;
    int b = 1;
    int c = 1;
    int d = 0;
    for(int i = 3; i <= n; i++){
        d = a + b + c;
        a = b;
        b = c;
        c = d;
    }
    return d;
}

3、118. 杨辉三角

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

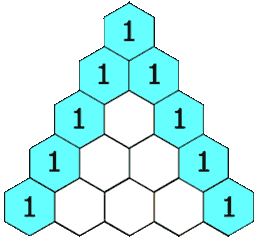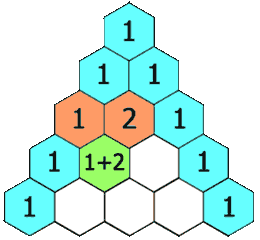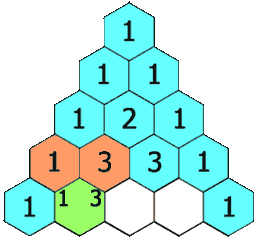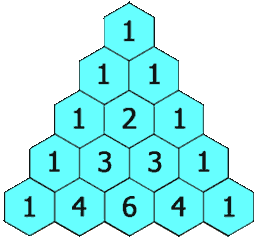
示例：

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

思路：

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
int** generate(int numRows, int* returnSize, int** returnColumnSizes){
    *returnSize = numRows;
    *returnColumnSizes = (int*)malloc(sizeof(int) * numRows);
    int** ans = (int**)malloc(sizeof(int*) * numRows);
    for(int i = 0; i < numRows; i++){
        ans[i] = (int*)malloc(sizeof(int) * (i + 1));
        (*returnColumnSizes)[i] = i + 1;
    }
    for(int i = 0; i < numRows; i++){
        for(int j = 0; j <= i; j++){
            if(j == 0 || i == j)
                ans[i][j] = 1;
            else
                ans[i][j] = ans[i-1][j] + ans[i-1][j-1];
        }
    }
    return ans;
}

4、119. 杨辉三角 II

给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

示例：

输入: rowIndex = 3
输出: [1,3,3,1]

思路：

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* getRow(int rowIndex, int* returnSize){
    *returnSize=rowIndex+1;
    int* num=(int*)malloc(sizeof(int)*(rowIndex+1));
    for(int i=0;i<=rowIndex;i++){
        for(int j=i;j>=0;j--){
            if(j==0||j==i)
            num[j]=1;
            else
            num[j]=num[j]+num[j-1];
        }
    }
    return num;
}

5、70. 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

思路：

int climbStairs(int n){
    if(n <= 2)
        return n;
    int a = 1;
    int b = 2;
    int c = 3;
    for(int i = 4; i <= n; i++){
        a = b;
        b = c;
        c = a + b;
    }
    return c;
}

6、剑指 Offer 62. 圆圈中最后剩下的数字

0,1,···,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字（删除后从下一个数字开始计数）。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

示例：

输入: n = 5, m = 3
输出: 3

思路：当只有两个数的时候，剩下的数是：(start + m) % 2;  start 是开始报数的下标位置
比如：0、1，m = 3，剩下的数的下标是(start + 3) % 2 = 1; start = 0
所以可以转化为递归，n个数中剩下的数是以n-1个数中剩下的数为开始进行一次报数后留下的数，
f(n,m)=(f(n-1,m),m)%n;

1. 递归

 
// 递归
 int f(int n, int m){
     if(n == 2)
         return m % n;
     return (f(n-1, m) + m) % n;
 }
 
 int lastRemaining(int n, int m){
     return f(n,m);
 }

        2.循环

// 也可以用循环的方式，从后往前，从只有两个数的时候开始，记下剩下的数的下标，作为下次的起点坐标
// 迭代
int lastRemaining(int n, int m){
    int ans = 0;
    for(int i = 2; i <= n; i++){
        ans = (ans + m) % i;
    }
    return ans;
}

7、剑指 Offer II 092. 翻转字符

如果一个由 '0' 和 '1' 组成的字符串，是以一些 '0'（可能没有 '0'）后面跟着一些 '1'（也可能没有 '1'）的形式组成的，那么该字符串是 单调递增 的。

我们给出一个由字符 '0' 和 '1' 组成的字符串 s，我们可以将任何 '0' 翻转为 '1' 或者将 '1' 翻转为 '0'。

返回使 s 单调递增 的最小翻转次数。

示例：

输入：s = "00110"
输出：1
解释：我们翻转最后一位得到 00111.

思路：0的前面只能是0，1的前面随便。动态规划。

#define MIN(a,b) a < b ? a : b
 
// 0的前面只能是0，1的前面随便
// dp[i][0] 表示前i个以0结尾的字符串需要翻转的次数
// dp[i][1] 表示前i个以1结尾的字符串需要翻转的次数
// int minFlipsMonoIncr(char * s){
//     int len = strlen(s);
//     int dp[len][2];
//     dp[0][0] = (s[0] == '0' ? 0 : 1); 
//     dp[0][1] = (s[0] == '1' ? 0 : 1);
//     for(int i = 1; i < len; i++){
//         dp[i][0] = dp[i-1][0] + (s[i] == '0' ? 0 : 1);
//         dp[i][1] = MIN(dp[i-1][0],dp[i-1][1]) + (s[i] == '1' ? 0 : 1);
//     }
//     return MIN(dp[len-1][0],dp[len-1][1]);
// }
 
int minFlipsMonoIncr(char * s){
    int len = strlen(s);
    int dp0 = 0;
    int dp1 = 0;
    for(int i = 0; i < len; i++){
        int dp00 = dp0;
        int dp11 = MIN(dp0,dp1);
        if(s[i] == '0'){
            dp11++;
        }else{
            dp00++;
        }
        dp0 = dp00;
        dp1 = dp11;
    }
    return MIN(dp1,dp0);
}

8、剑指 Offer II 098. 路径的数目

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例：

 

输入：m = 3, n = 7
输出：28

思路：动态规划

int uniquePaths(int m, int n){
    if(m == 1 || n == 1)
        return 1;
    int dp[m][n];
    dp[0][0] = 0;
    for(int i = 1; i < m; i++){
        dp[i][0] = 1;
    }
    for(int i = 0; i < n; i++){
        dp[0][i] = 1;
    }
    for(int i = 1; i < m; i++){
        for(int j = 1; j < n; j++){
            dp[i][j] = dp[i-1][j] + dp[i][j-1];
        }
    }
    return dp[m-1][n-1];
}

文首图片素材取自博客：《算法零基础100讲》(第28讲) 递推问题_英雄哪里出来的博客-CSDN博客