[TIST 2022]No Free Lunch Theorem for Security and Utility in Federated Learning

联邦学习中的安全性和实用性没有免费午餐定理
No Free Lunch Theorem for Security and Utility in Federated Learning

摘要

在多方共同从各自的数据中学习模型的联邦学习场景中，选择合适的算法存在两个相互冲突的目标。一方面，在半诚实的合作伙伴在场的情况下，必须尽可能保证隐私和敏感训练数据的安全；另一方面，为了学习效用，必须在各方之间交换一定量的信息。这样的挑战需要保护隐私的联邦学习解决方案，它可以最大限度地发挥学习模型的效用，并为参与方的私人数据保持可证明的隐私保证。

本文阐述了一个通用框架，该框架 (1) 从统一信息论的角度制定了隐私损失和效用损失之间的权衡，以及 (2) 描述了不同保护机制下隐私效用权衡的量化界限包括随机化、稀疏性和同态加密。结果表明，一般来说，隐私与效用的权衡没有免费的午餐，人们必须用一定程度的退化效用来交换保护隐私。本文中阐述的定量分析可以作为实用联邦学习算法设计的指导。

简介

现代机器学习技术需要大量数据，在开发大型预训练机器学习模型时使用万亿字节的数据并不少见，例如自然语言处理 [ 16、18 ]或图像处理[ 13、47 ] . 对于各种各样的机器学习应用程序，例如，在社交媒体或金融用例中，数据通常分布在多个设备或机构中。将此类数据收集到中央服务器上进行训练会产生额外的通信开销、管理和业务合规成本、隐私问题，甚至还有 GDPR（通用数据保护条例）等监管和司法问题。1联邦学习（FL） 已作为一种有效技术引入，允许多方联合训练模型，而无需在各方之间收集或交换私人训练数据。此外，还要求在学习或推理阶段交换的信息不会将各方拥有的私有数据泄露给半诚实的对手（正式定义见第2.2.1节），半诚实的对手旨在监视或推理其他方’ 来自交换信息的私有数据。如本文所述，这些要求构成了保护隐私 FL 的新型统计框架的主要任务。

从信息论的角度来看，半诚实方可以从交换的信息中推断出的有关私人数据的信息量本质上取决于私人数据和公开交换的信息之间的统计依赖性。最近的研究表明，半诚实的对手可以利用这种依赖性从学习模型的交换梯度中恢复具有像素级精度的私人训练图像，例如通过使用贝叶斯推理攻击（参见第3.3节和其他作品[ 41、89、90 ] 了解详情）。考虑到此类威胁模型，我们因此重申安全联邦学习 (SFL)方案必须（1）支持多方联合训练模型并在不交换私有数据的情况下进行联合推理，以及（2）明确定义威胁模型和这些模型下的安全保证。

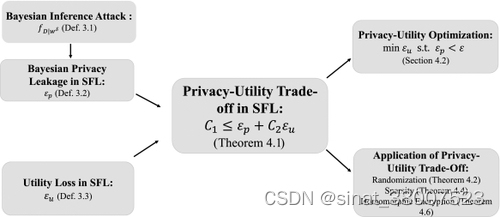
在本文中，我们考虑水平 FL [ 81 ] 或跨设备 FL [ 46 ] 设置，其中多个客户端将各自的本地模型或模型更新上传到聚合器2 ，聚合器2负责将多个本地模型聚合到一个全球模型。有多种应用场景将此方案用于FL [ 56、57、82 ]。基本的隐私保护要求是保持潜在的隐私损失低于可接受的水平。这是通过减少交换的模型信息和私有数据之间的依赖关系来实现的。然而，与未使用任何保护训练的全局模型相比，减少的依赖性使得聚合全局模型的准确性降低并导致效用损失，例如模型准确性的损失。严重退化的模型效用确实首先违背了 FL 的目的。因此，我们在本文中提出了一个统一的统计框架，以在严格的理论基础上分析隐私与实用程序的权衡。我们研究的主要结果总结如下

• 首先，我们通过贝叶斯推理攻击的角度（定义3.1）[ 29、79 ]来制定隐私泄露攻击[ 41、89、90 ]。然后提出了一种称为贝叶斯隐私的隐私度量来量化半诚实的对手可能通过观察公开交换的信息而获得的关于私人数据的额外信息量。具体来说，对手的信息增益——即贝叶斯隐私泄露（定义3.2 ）——是通过对手的先验分布和后验分布之间的距离来衡量的关于私人数据的信念。此外，贝叶斯隐私泄漏的上限称为ε-贝叶斯隐私提供隐私保护保证，无论半诚实的对手可能发起任何贝叶斯推理攻击。

• 其次，我们提出了一个统计框架，将最佳隐私效用权衡转化为约束优化问题，其中效用损失（定义3.3）在贝叶斯隐私泄露的预设上限（即ε-贝叶斯隐私）约束（参见第4.2节）。然后，权衡的理论分析表现为定理4.1，它规定 (1) 隐私损失和效用损失的加权和大于依赖于问题的非零常数，以及 (2) 之间的相对权重隐私损失和效用损失取决于多种因素，包括对手可能发起的贝叶斯推理攻击、采用的保护机制以及训练和测试数据的分布。换句话说，原则上必须以一定程度的效用损失增加来交换隐私损失的减少，反之亦然。3个

• 第三，应用定理4.1的一般原理，定量分析特定隐私保护机制下的权衡，包括随机化[ 1,34,75 ]、稀疏性[38,69,70 ]和同态加密（HE） [ 31 , 84 ]（参见定理4.2、4.4和4.6). 这些理论上合理的结果在他们自己的权利中是令人感兴趣的。然而，它们在为各种场景下的 FL 算法设计提供实用指导方面具有实用价值（应用见4.3节）。

据我们所知，所提出的贝叶斯隐私公式是第一个明确考虑威胁模型（攻击机制）和安全模型（保护机制）的统一框架。它也是第一个适用于不同隐私保护机制的方法，包括随机化[ 1、34、75 ] 、稀疏性[ 38、69、70 ]和HE [ 31、84 ]。本文的其余部分组织如下。第2节回顾了与隐私测量和 FL 相关的现有工作。第三节_说明了基于贝叶斯推理攻击和保护机制的统计框架。第4节说明了隐私效用权衡的量化（定理4.1 ），第4.3节进一步介绍了权衡在不同保护机制上的应用。第5节介绍了贝叶斯隐私与其他隐私测量的比较。最后，第6节总结了文章，讨论了未来的研究计划。

2 相关文献

本节从不同方面简要回顾相关工作，包括隐私度量、FL 中的隐私攻击和保护方法，以及隐私-效用权衡。

2.1 隐私测量

隐私保护计算的需求出现在各种应用程序中，从数据库挖掘、通过公共渠道传递秘密信息，到最近的机器学习。文献中提出的隐私或隐私测量的众多定义可以大致分为以下两类：先验独立定义和先验依赖定义：

• 差分隐私 (DP)是由 Dwork 等人提出的著名的先验独立定义。以保护个人隐私以响应有关数据库的查询[ 21、23、25 ] 。随后提出了一系列 DP 变体来收紧各种条件下的隐私预算，包括具有 DP 自然松弛的 Renyi DP [ 59 ] 和具有封闭形式隐私边界和更强保证的 Gaussian DP [ 11 ]。此外，已经设计了大量算法来在 FL [ 67、75 ]和 Abadi 等人中实现DP。[ 1] 提出了适合深度学习的DP的moments accountants。我们建议读者参考其他作品 [ 22、39 ] ，以全面了解基于 DP 的隐私保护。值得一提的是，基于 DP 的测量没有考虑私有数据的先验分布——也就是说，DP 及其变体是先验独立的，除了贝叶斯差分隐私 (BDP) [ 73 ]。

• 在不同的先验相关隐私测量 [ 3、19、45 ] 中，信息隐私( IP ) [ 19 ] 被提议根据对手在观察数据后学到的关于私有数据的“知识量”对隐私泄漏进行建模。用户的输出。然后，根据速率失真理论[ 5、71 ] ，将最佳隐私与效用权衡作为优化问题，以最小化受效用损失约束影响的信息泄漏。用于量化信息泄漏的分歧包括Kullback-Leibler (KL) 散度（互信息）[ 19 ]、卡方散度[ 43 ]、全变散度[ 62 ]和人义散度[ 53 ]。

2.2 联邦学习

FL 的概念最初是由 McMahan 等人提出的。目的是基于分布在多个设备上的数据集构建机器学习模型[ 49、50、56、57 ]。主要思想是聚合在多个设备上学习的本地模型，但不将私有数据发送到半诚实的第三方服务器或其他设备。考虑到跨多个机构分布的秘密数据的隐私问题，Yang 等人。[ 81 ]将 FL 的应用扩展到广泛的用例，并将 FL 场景分为三类：

(1)横向联邦学习：数据集共享相同的特征空间，但样本空间不同。

(2)纵向联邦学习：两个数据集共享相同的样本 ID 空间，但特征空间不同。

(3)联邦迁移学习：两个数据集不仅样本不同，特征空间也不同。

杨等[ 81 ]还提出了 SFL 的概念，以强调保护训练数据隐私免受各种对手攻击的重要性。在 Kairouz 等人的工作中，水平和垂直 FL 也分别称为跨设备FL和跨孤岛 FL[ 46 ]。已经提出了以下大量文献来提高隐私保护能力和模型效用。

2.2.1 FL 中的威胁模型。

为了隐私安全，通常需要考虑 FL 中存在半诚实（诚实但好奇）的对手。对手是诚实的，因为他或她忠实地遵循协作学习协议并且不提交任何格式错误的消息，但他或她可能会发起隐私攻击以通过分析联合模型的定期更新来窥探其他参与者的训练数据（例如，梯度）在训练期间。这种攻击被称为贝叶斯推理攻击（请参考定义3.1），根据半诚实攻击者利用的信息源，可以大致分为：

• 梯度反转攻击：Zhu 和 Han [ 89 ] 以及 Zhu 等人[ 90 ] 表明，深度泄漏攻击允许对手从交换的深度神经网络模型梯度中将私有数据恢复到像素级精度。在这项开创性的工作之后，表明对手可以通过进一步利用各种先验来发起更有效的攻击，例如通过全变损失 [ 28 ] 的图像平滑度先验、图像标签先验 [ 87 ] 和估计图像的组一致性 [ 83 ]。

• 来自输出的模型反转攻击：拆分学习[ 38 ] 允许机器学习模型被分离并在计算资源较低的多个客户端上进行训练，其中每个客户端仅训练拆分模型的一小部分（例如，几层神经网络） . 然而，在这种情况下，对手仍然可以从模型输出中推断出私人数据[ 27、41 ]。顾等。[ 37 ] 后来在联合分裂学习（称为SplitFed）设置中应用了模型反转攻击[ 70 ]，其中客户端仅将部分信息上传到服务器。

• 基于生成对抗网络的攻击：生成对抗网络用于推断客户的私人数据。希塔吉等人[ 42 ] 将聚合模型视为生成对抗网络的鉴别器，以生成特定类别的分布。王等[ 78 ]提出学习一个生成器，除了特定类的数据分布之外，它还可以恢复用户指定的私有数据。

2.2.2 FL 中的保护机制。

为了保护隐私数据不被对抗性攻击泄露，SFL 4采用了以下保护机制：

• 随机化：通过向模型信息添加拉普拉斯噪声或高斯噪声 [ 23 ] ，DP已被广泛用于保护 FL [ 1、34、75 ]中的交换信息。还提出了局部 DP [ 21 ] 以随机化 FL [ 67、75、88 ]中的响应。尽管它简单且流行，但随机化方法不可避免地会在收敛速度慢、模型效用低和隐私保证松散方面导致性能下降，如其他地方所述[ 44、48、73 ]等。

• 加密：加密是一种广泛采用的保护敏感信息的技术。特别是，HE及其变体 [ 31、32、64 ]允许直接在加密的本地模型上执行FL模型的聚合，而无需解密[ 2、74、85、86 ]。然而，HE 带来的极其繁重的计算和通信开销使其无法轻松应用于大型模型，例如具有数十亿模型参数的深度神经网络。提出高效的 HE 算法来提高 FL 效率仍然是一个活跃的研究课题 [ 2 , 84].

• 基于稀疏性的方法：这些方法通过隐藏部分信息不与其他方交换来保护客户的私人数据 [ 69 ]。特别是，联邦设置中的拆分学习提出将部分神经网络模型与其他方 [ 38 ] 分离和隐藏，而 SplitFed [ 70 ] 将拆分学习和 FL 结合起来，同时提高效率和效用。

• 秘密共享：秘密共享 [ 4、6、68 ]是为了在一组参与者之间分发秘密而开发的。然而，它需要大量的消息交换，并且需要大量的通信开销，这在许多 FL 设置中是不可行的。

一些保护机制（例如，[ 51 ]）不属于 FL 领域，超出了我们文章的范围。

2.3 隐私-实用权衡

在过去的十年中，人们对理解隐私与效用权衡的文献产生了广泛的兴趣：

一些工作侧重于隐私与效用的权衡，其中效用通过失真（准确性）量化（反向），隐私通过 IP 量化。桑卡尔等[ 65 ] 对数据库中个人隐私需求与已发布数据的效用之间的权衡进行了精确量化。Makhdoumi 和 Fawaz [ 55 ] 根据 Calmon 和 Fawaz [ 19 ]提出的框架对隐私-效用权衡进行建模。他们将权衡视为凸优化问题，其目的是在发布数据的效用（失真）约束下最小化私有数据和发布数据之间的互信息。此外，Rassouli 和 Gündüz [ 62] 进一步使用总变差定义了隐私，并说明了可以使用标准线性程序解决最佳隐私-效用权衡问题。此外，Wang 和 Calmon [ 77 ] 在使用χ2个基于信息的措施。

Dwork 和 Naor [ 24 ]认为实用性和宽松的隐私保护能力的权衡对于有用的查询是必要的，她还给出了一个定量分析与( ε , 0 )-DP 的最大误差（在效用中）为欧姆（1个ε)[ 25 ]。DP预算ε隐私保护算法的研究后来与隐私保护算法的收敛性（效用）相关 [ 35 , 76 ]。

总而言之，在现有工作中，我们发现迫切需要为设计新颖的 FL 算法奠定坚实的基础。特别是最近的贝叶斯推理威胁类型[ 28、83、87、89、90] 没有被现有的隐私定义明确建模，例如 DP，它被认为是隐私的黄金标准定义。缺乏严格的公式使得从业者不清楚如何确定有关隐私实用权衡的算法设计的最佳选择。目前还没有同时考虑不同保护机制（包括随机化和 HE）的框架。因此，本文的其余部分将说明这种基于贝叶斯推理攻击的新型统计框架，旨在解决上述现有工作中未妥善解决的问题。

3 一般设置和框架

3.1 符号

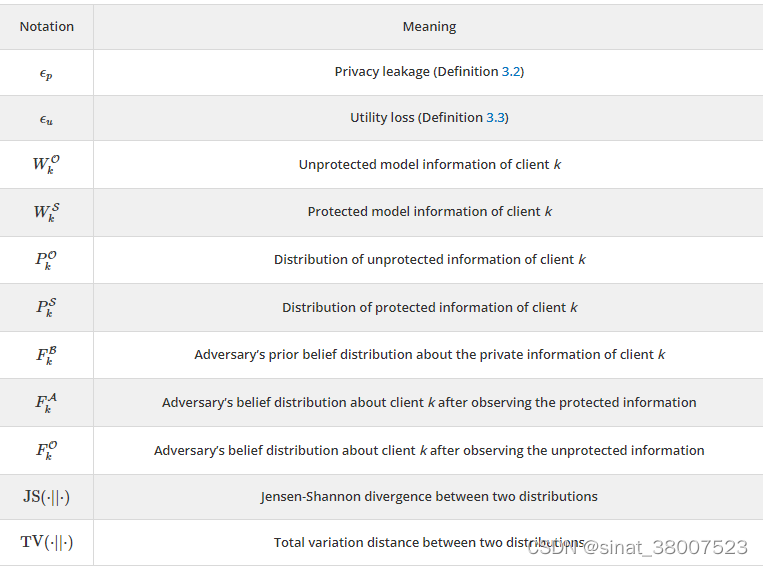
3.2 一般设置

在这项工作中，我们考虑了一个水平 FL场景，或跨设备 FL [ 46 ]，其中多个 ( K ) 参与者5协作学习全局模型而不公开他们的私人训练数据[ 56、81 ]。对私有数据采取一定保护的要求是由于威胁模型。一些半诚实的对手可能会对交换的信息发起隐私攻击，以推断其他参与者的私人数据（半诚实对手的正式定义，请参见第2.2.1节）). 最初，服务器将全局模型信息分发给所有客户端。整个 SFL 程序如图2的左侧面板所示，总结如下：


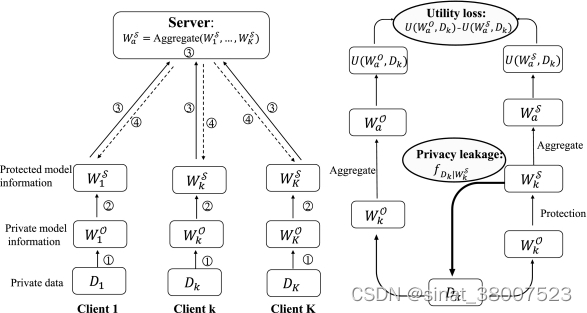
注：在 SFL 中，本地模型信息包括模型参数、模型梯度和模型输出，所有这些信息都可以选择性地交换给聚合器并暴露给半诚实的对手（详见附录B）。保护机制M的目标是保护私有数据，

在此 SFL 设置中，考虑了图2右侧面板中所示的隐私损失和效用损失：

(1)为了保护隐私，贝叶斯隐私泄漏度量（见定义3.2）用于量化尽管对公开信息应用了保护机制，但半诚实的对手仍可能推断出的有关私人数据的信息量。贝叶斯隐私泄漏允许人们评估安全联邦学习方案的安全性，并证明如果贝叶斯隐私泄漏小于可接受的阈值（请参阅第4.2节），所采用的保护机制在阻止贝叶斯推理攻击方面是安全的。

(2)保护机制修改原有模型信息到其受保护的对手并导致局部模型的行为不太准确。因此，汇总的全球模型不太准确，所发生的公用事业损失被定义为有保护和没有保护的公用事业的差异（定义3.3）。

3.3 SFL 中的贝叶斯推理攻击

结果表明，半诚实的对手可以从学习模型的无保护梯度中恢复隐私训练图像，精度达到像素级，例如通过使用有效的贝叶斯推理攻击 ([ 41 , 89 ])。我们假设对手



注：

(1) 这里定义的贝叶斯推理攻击是半诚实参与者假设的具体实现。攻击者从其他方获悉信息，并试图推断出其他方持有的隐私信息。然而，攻击者不会主动在交换的消息中注入信息以获取更多私人信息或“毒害”联合模型。

(2)要求*贝叶斯推理攻击的时间成本是多项式的。*鉴于此要求，*如果攻击成本呈指数增长，*例如针对 HE [ 31 ]，对手将无法获得有关客户端私有数据的任何其他信息。从实用的角度出发，在附录B.4中我们对贝叶斯推理攻击进行了详细分析，包括梯度反转攻击、模型反转攻击和针对不同保护机制的暴力攻击。

(3)我们从贝叶斯推理的角度制定了三种攻击，包括梯度逆攻击 [ 28、83、87、89 ]、模型反转攻击 [ 27、41 ]和蛮力攻击（尤其是加密）（详见附录B） . 这些攻击方法在暴露信息的类型上有所不同，包括 SFL 中的模型、模型梯度和模型输出。此外，先验（表示为F乙k) 是推断私有数据的重要因素。例如，如果攻击者知道图像的标签是“猫”，他或她可能会使用平均的“猫”图像来初始化恢复图像并显着提高恢复数据的准确性（先验对攻击的影响是如附录B.1.1所示）。

3.4贝叶斯隐私泄露

贝叶斯隐私泄露衡量了对手在有和没有泄露信息的情况下的信念之间的差异。此外，贝叶斯隐私泄漏是相对于暴露给对手的受保护模型信息变量进行平均的。

注：与KL散度不同，JS散度是对称的，其平方根满足三角不等式 [ 26 ]。此属性允许导出定理4.1中说明的主要结果。贝叶斯隐私泄露的定义可以概括为对客户端的最大隐私泄露。

3.5 SFL 中的效用损失

除了隐私泄露，我们工作中调查的另一个重要问题是效用损失，其定义如下。

注：模型效用评估各种学习任务的模型性能。例如，模型效用是分类问题中的分类准确度和回归问题中的预测准确度。

4 隐私-效用权衡的一般框架

在第3节中，我们介绍了 SFL 中隐私泄漏和效用损失的定义。在本节中，我们首先对贝叶斯隐私泄漏和效用损失之间的权衡进行严格分析（天下没有免费的午餐定理）。然后我们将隐私-效用权衡制定为一个优化问题，使效用损失最小化ε-贝叶斯隐私约束。最后，我们将贝叶斯隐私泄露和效用损失之间提出的没有免费午餐定理应用到 SFL 的四种保护机制中。

4.1 隐私-效用权衡的理论分析

隐私保护的思想是修改未受保护的信息，保证隐私数据不会泄露给半诚实的敌手。




注：

(1)该假设意味着定义4.2中定义的接近最优参数的累积密度是有界的。该假设排除了效用函数在最优参数和特定部分参数之间保持不变或无法区分的情况。

(2)注意△k独立于对手的威胁模型，并且△k当保护机制、效用函数和数据集固定时，是常数。
下面的定理代表了这项工作的中心结果。作为没有免费午餐定理的一种形式，它指出在我们的半诚实 SFL 设置中联合模型的隐私保护和效用增强受常数限制。如果增加隐私保护，则可能会失去联合模型的一些效用，反之亦然。

定理4.1说明客户端的平均隐私泄漏和效用损失的总和受问题相关常数的下限。如图3所示，等式（6）是基于贝叶斯隐私泄露（定理4.1）中采用的JS测度的三角不等式。它本质上是指必须以减少隐私泄漏为代价（εp) 随着效用损失的一定程度增加 (ε你), 反之亦然。这一原则与优化和机器学习的没有免费午餐定理 [ 80 ]有着有趣的相似之处，它致力于“如果算法在某一类问题上表现良好，那么它必然会为所有问题的性能下降付出代价”剩下的问题。” 因此，我们在 FL 中将等式 ( 6 ) 命名为“没有免费的午餐定理 (NFL)”。

注：$\text{TV}(P_k^{\mathcal{O}}||P_k^{\mathcal{S}})$ 中的保护机制根据应用和未应用保护方法的模型信息分布之间的距离提供了保护机制带来的修改的上限。

4.2 隐私保护优化

在保护隐私的机器学习场景中，客户旨在保持最大可能的模型效用，同时不泄露超出可接受水平的私人信息。我们可以将这种权衡视为一个优化问题。目标是在隐私保护约束下最小化效用损失。让贝叶斯隐私泄露εp定义为定义3.2。我们说 SFL 系统保证ε-贝叶斯隐私，如果它认为 ${ϵ}_p\le ϵ$
ε-贝叶斯隐私保证SFL系统的贝叶斯隐私泄露永远不会超过规定的阈值ε作为安全要求。对于联邦机器学习系统，目标是找到一种保护机制M，使聚合效用损失最小。这两个要求可以转化为保护机制的约束优化问题：

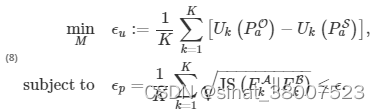
注：
(1)常量ε等式（8）中的强加提供了一种可以实现的隐私安全保证，而不管对手可能发起的各种贝叶斯推理攻击。

(2)这个受约束的优化问题与优化公式 [ 19 ] 密切相关，后者旨在最大限度地减少信息泄漏，同时保证效用损失小于给定阈值。

4.3 隐私-效用权衡的应用

在本节中，我们将贝叶斯隐私泄露和效用损失之间的免费午餐定理应用于四种隐私保护机制：随机化 [ 1 , 34 , 75 ]、稀疏性 [ 38 , 69 , 70 ]、HE [ 31 , 84 ]和秘密共享 [ 4 , 6 , 68 ]。9我们分析了特定保护机制参数对隐私泄露和效用损失波动的影响。

4.3.1 随机化机制。

随机化机制是一种自然选择，因为它的噪声参数（例如，σ)允许灵活地控制权衡。在 SFL 中，其中一种随机化方法是将随机噪声（例如高斯噪声）添加到模型梯度中[ 1,34,75 ]。




因此，至少C1个由于未受保护的模型信息暴露给可能发起贝叶斯推理攻击的对手，可能会导致隐私泄露。这一理论分析与别处展示的经验证据一致 [ 41 , 89 ]。

4.3.2 稀疏机制。

隐私和效用之间的权衡随着稀疏程度的不同而变化。在 SFL 中，客户端通过将部分参数上传到服务器来启动稀疏机制。具体来说，每个客户端将总共n 个维度中的d个上传到服务器。

以下定理使用上传模型信息d的维度说明了隐私泄露和效用损失的界限。完整的证明推迟到附录C.2。


Proposition 4.5. 对于通过向服务器上传部分信息的稀疏机制，我们有以下内容：

命题4.5论证了当上传模型信息d的维度增加时，贝叶斯隐私泄露的下界εp增加，效用损失的上限ε你减少。d= n 意味着服务器将所有参数上传到服务器

4.3.3 同态加密。

HE [ 31 , 32 , 64 ] 允许直接对密文执行某些计算（例如，加法），而无需先解密它们。这种特性允许将 HE 应用到 FL 中以保护隐私，因为服务器只访问密文上的用户上传参数，而不是直接访问客户端的明文 [ 2 , 74 , 85 , 86 ]。具体而言，在 FL 中，上传的模型权重或梯度已由客户端自行加密。因此，对手很难窥探暴露的信息并推断出客户的私人数据。下面的定理评估了近似特征向量的隐私泄露和效用损失方法的隐私泄漏和效用损失[ 33]，这是一种广泛使用的HE方法。

备注：
(1)一方面，如果私钥未知，贝叶斯隐私泄露${\epsilon }_p$为零，因为加密满足语义安全，其中$D_k$独立于$W_k^S$. 而且，由于 HE 的私钥是未知的，全局模型$\text{Enc}(W_a^{\mathcal{O}})$保持加密状态，服务器评估的效用与最佳效用相去甚远（效用损失大）。

(2)另一方面，如果私钥被错误地泄露给服务器（对手），则服务器可以解密全局模型和效用损失${ϵ}_u=0$在理想情况下。此外，隐私泄露${\epsilon }_p$很大。

4.4 秘密分享

秘密共享[ 4,6,68 ]是为了在一组参与者之间分发秘密而开发的。然而，它需要大量的消息交换，并且需要大量的通信开销，这在许多 FL 设置中是不可行的。让$W_k^{\mathcal{O}}$表示服从均匀分布的原始模型信息

注：对于秘密共享机制，不存在隐私和效用之间的连续权衡，但定理4.1中的等式（ 5 ）仍然成立。

5 讨论

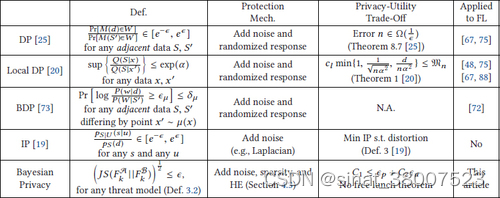
本节说明了所提出的贝叶斯隐私与 DP [ 25 ]、BDP [ 73 ]、本地 DP [ 20 ] 和 IP [ 19 ] 的比较。表2总结了比较的简要总结。

5.1 与 DP 及其变体的比较

我们说明贝叶斯隐私相对于 DP 及其变体的比较如下：

• 首先，在 DP 中分析的隐私-效用权衡本质上以倒数关系为特征，如 Dwork 和 Roth [ 25 ] 的定理 8.7 所示，它表明输出受保护ε-差分隐私机制具有最大误差$\Omega (\frac{1}{ϵ})$. 这种权衡分析与本文中的没有免费午餐定理（定理4.1）形成对比，后者规定隐私损失和效用损失的总和大于问题相关常数。

• 其次，表明一个ξ-最大贝叶斯隐私保护映射$f_{W|S}(\cdot )$是( 2 ξ)- 差分隐私（详见附录D）。

• 第三，由本地 DP 建立的隐私实用权衡致力于，对于α-private estimator，它的效用的最小误差边界正比于$\frac{1}{{\alpha }^2}$（参见 Duchi 等人 [ 20 ] 的工作中的定理 1）。

• 第四，还提出了 BDP 来衡量遵循贝叶斯规则的隐私损失 [ 20 ]。然而，BDP 估计了给定私有数据（由x表示）的查询输出（由S表示）的后验。这与提议的贝叶斯隐私形成鲜明对比，贝叶斯隐私模拟对手在给定公开交换信息（表示为$W^{\mathcal{S}}$). 此外，在 Duchi 等人的工作中，没有为 BDP 提供隐私-效用权衡分析。[ 20 ]。

• 最后但同样重要的是，DP 及其变体不适合将加密作为一种保护机制。据我们所知，基于贝叶斯推理攻击的 SFL 框架是第一个适用于不同隐私保护机制的框架，包括 DP [ 1、34、75 ] 中的随机化、稀疏性[ 38、69、70 ]、HE [ 31 ] , 84 ] 和秘密共享 [ 4 , 6 , 68 ]。

5.2 贝叶斯隐私与知识产权的关系

贝叶斯隐私和 IP [ 19 ]之间存在三个根本区别，如下所示：

• 贝叶斯隐私和 IP 之间的一个根本区别在于贝叶斯隐私是在第3节中说明的 SFL 设置中制定的，尽管目前尚不清楚如何应用 IP 来描述分布式学习场景中的隐私-效用权衡。

• 根据隐私定义，贝叶斯隐私涉及对手可能通过观察公开暴露的模型信息获得的关于私人数据的信息的平均增益（参见本文中的定义3.2）。然而，IP 是基于此类信息增益的界限来定义的（参见 Calmon 和 Fawaz [ 19 ] 著作中的定义 6）。请注意，我们还在等式 ( 7 ) 中给出了贝叶斯隐私的界限，但它仍然基于平均增益。

• 在隐私-效用权衡方面，贝叶斯隐私的最佳权衡被视为约束优化的解决方案，其目标是在保持贝叶斯隐私泄漏小于可接受的硬约束下最小化效用损失阈值（等式（8）中的问题）。相比之下，IP 中的最佳权衡是在给定的效用损失约束下最小化隐私泄漏（Calmon 和 Fawaz [ 19 ] 工作中的定义 3）。

注：值得注意的是，贝叶斯隐私是使用 JS 散度而不是 KL 散度来衡量的。与KL散度不同，JS散度是对称的，其平方根满足三角不等式。JS散度的三角不等式的性质有助于推导我们在第4.1节中说明的主要结果。

6 结论

在本文中，我们提出了一个基于贝叶斯推理攻击的 SFL 统计框架，以考虑到两个迫切的要求：隐私数据的保护以及 SFL 中模型效用的最大化。所提出的框架基于贝叶斯隐私泄漏的基石定义，该定义定量测量半诚实的对手在 SFL 学习过程中可能从间谍信息中推断出的有关私人数据的信息量。然后权衡隐私和效用被表述为一个优化问题，其目标是找到交换模型信息的修改分布，以实现最小的效用损失，而不会导致隐私损失超过可接受的水平。然后，权衡的理论分析将我们引向 FL 的没有免费午餐定理，这表明人们必须以一定程度的效用损失来换取高隐私持久性保证，反之亦然。这种权衡分析适用于包括随机化在内的保护机制[1 , 34 , 75 ] 、稀疏性[38,69,70 ]、HE[ 31,84 ]和秘密共享[ 4,6,68 ]，它们是定理4.1中证明的一般定理的特例。

据我们所知，SFL 中隐私实用权衡的分析是第一项在统一框架中考虑不同特定保护机制（包括 DP 和 HE）的工作。尽管本文中披露的主要结果令人鼓舞，但我们计划应用我们在这项研究工作中开发的技术，在未来探索效率和隐私之间的权衡，从而提供更全面的 SFL 视图。