深度学习 Day 12——利用卷神经网络实现MNIST手写数字的识别

深度学习 Day 12——利用卷神经网络实现MNIST手写数字的识别

一、前言

• 🍨 本文为🔗365天深度学习训练营 内部限免文章（版权归 K同学啊 所有）
• 🍦 参考文章地址： 🔗深度学习100例-卷积神经网络（CNN）实现mnist手写数字识别 | 第1天
• 🍖 作者：K同学啊 | 接辅导、程序定制

在上一周深度学习的博客中，我们了解学习了利用卷神经网络进行彩色图片的分类，也了解到了什么是CNN网络，并学会如何构建CNN网络。

有关CNN知识可以移步到我的学习专栏里面去了解：

Python深度学习专栏

本周我们继续使用CNN，来完成mnist手写数字的识别任务。

二、我的环境

• 电脑系统：Windows 11
• 语言环境：Python 3.8.5
• 编译器：DataSpell 2022.2
• 深度学习环境：TensorFlow 2.3.4
• 显卡及显存：RTX 3070 8G

三、前期工作

1、设置GPU并导入依赖项

和之前一样，如果你GPU很好就只使用GPU进行训练，如果GPU不行就推荐使用CPU训练加GPU加速。

只使用GPU：

import tensorflow as tf
gpus = tf.config.list_physical_devices("GPU")

if gpus:
    gpu0 = gpus[0] #如果有多个GPU，仅使用第0个GPU
    tf.config.experimental.set_memory_growth(gpu0, True) #设置GPU显存用量按需使用
    tf.config.set_visible_devices([gpu0],"GPU")
1
2
3
4
5
6
7

使用CPU+GPU:

os.environ["CUDA_VISIBLE_DEVICES"] = "-1"
1

导入依赖项：

import os
import tensorflow as tf
from tensorflow.keras import datasets, layers, models
import matplotlib.pyplot as plt
1
2
3
4

2、MNIST手写数字数据集

MNIST数据集是一个缩写词，代表修改后的美国国家标准与技术研究所数据集。

它是一个包含 60,000 个 0 到 9 之间的手写个位数的小正方形 28×28 像素灰度图像的数据集。

任务是将给定的手写数字图像分类为代表从 0 到 9 的整数值的 10 个类别之一，包括 0 到 9。

它是一个广泛使用和深入理解的数据集，并且在很大程度上是“解决的”。表现最好的模型是深度学习卷积神经网络，其分类准确率达到 99% 以上，在保留测试数据集上的错误率在 0.4% 到 0.2% 之间。

3、导入数据并进行归一化

我们一般会采用(train_images, train_labels), (test_images, test_labels) = datasets.mnist.load_data()这样的方式直接调用，这样使用起来就比较简单。

# 导入mnist数据，依次分别为训练集图片、训练集标签、测试集图片、测试集标签
(train_images, train_labels), (test_images, test_labels) = datasets.mnist.load_data()

# 对数据进行归一化
# 将像素的值标准化至0到1的区间内。(对于灰度图片来说，每个像素最大值是255，每个像素最小值是0，也就是直接除以255就可以完成归一化。)
train_images, test_images = train_images / 255.0, test_images / 255.0
1
2
3
4
5
6

本期数据在导入之后会自动下载。

现在我们来查看一下我们的数据的维数信息：

print('训练集：x=%s, y=%s' % (train_images.shape, train_labels.shape))
print('测试集：x=%s, y=%s' % (test_images.shape, test_labels.shape))
1
2

它运行的结果是：

训练集：x=(60000, 28, 28), y=(60000,)
测试集：x=(10000, 28, 28), y=(10000,)
1
2

我们可以看到训练数据集中有 60,000 个示例，测试数据集中有 10,000 个示例，并且图像确实是 28×28 像素的正方形。

4、可视化手写数字图片

# 将数据集前20个图片数据可视化显示
# 进行图像大小为20宽、10长的绘图(单位为英寸inch)
plt.figure(figsize=(20,10))
# 遍历MNIST数据集下标数值0~49
for i in range(20):
    # 将整个figure分成5行10列，绘制第i+1个子图。
    plt.subplot(2,10,i+1)
    # 设置不显示x轴刻度
    plt.xticks([])
    # 设置不显示y轴刻度
    plt.yticks([])
    # 设置不显示子图网格线
    plt.grid(False)
    # 图像展示，cmap为颜色图谱，"plt.cm.binary"为matplotlib.cm中的色表
    plt.imshow(train_images[i], cmap=plt.cm.binary)
    # 设置x轴标签显示为图片对应的数字
    plt.xlabel(train_labels[i])
# 显示图片
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

5、调整图片格式

#调整数据到我们需要的格式
train_images = train_images.reshape((60000, 28, 28, 1))
test_images = test_images.reshape((10000, 28, 28, 1))
1
2
3

四、构建CNN网络模型

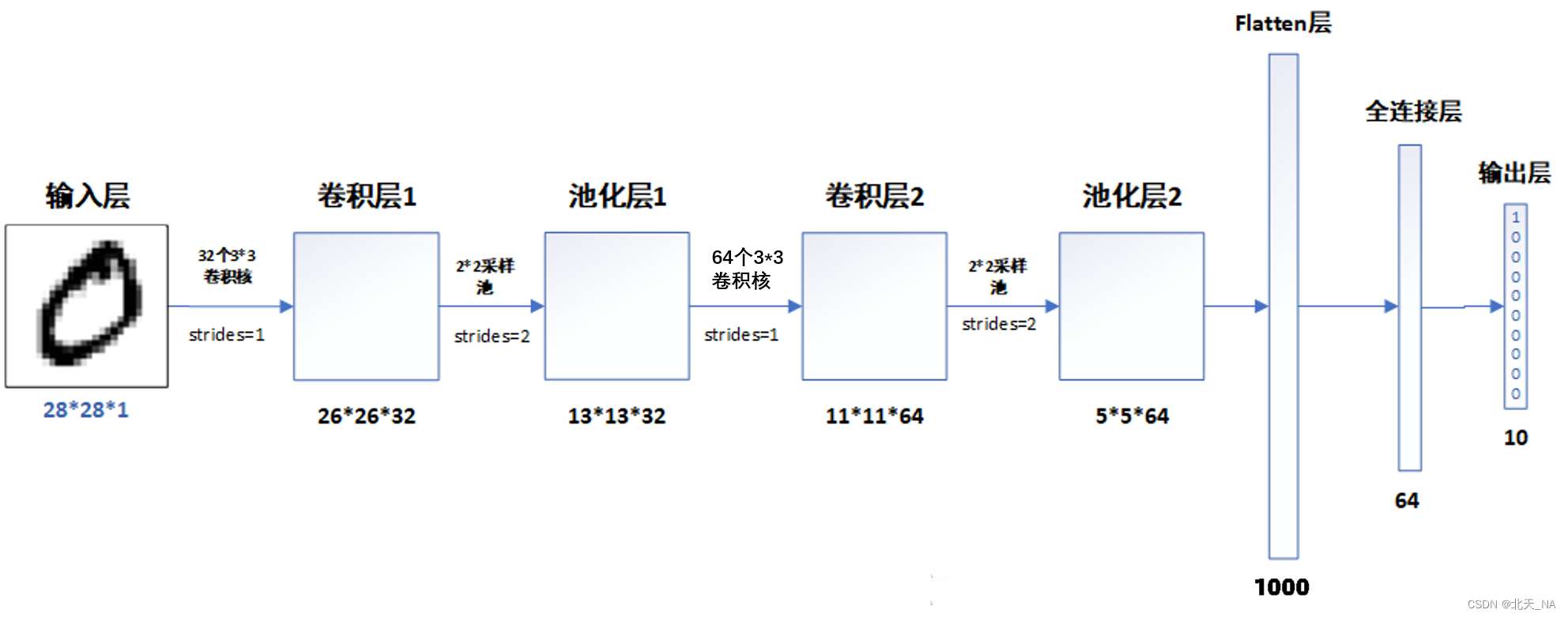
# 创建并设置卷积神经网络
# 卷积层：通过卷积操作对输入图像进行降维和特征抽取
# 池化层：是一种非线性形式的下采样。主要用于特征降维，压缩数据和参数的数量，减小过拟合，同时提高模型的鲁棒性。
# 全连接层：在经过几个卷积和池化层之后，神经网络中的高级推理通过全连接层来完成。
model = models.Sequential([
    # 设置二维卷积层1，设置32个3*3卷积核，activation参数将激活函数设置为ReLu函数，input_shape参数将图层的输入形状设置为(28, 28, 1)
    # ReLu函数作为激活励函数可以增强判定函数和整个神经网络的非线性特性，而本身并不会改变卷积层
    # 相比其它函数来说，ReLU函数更受青睐，这是因为它可以将神经网络的训练速度提升数倍，而并不会对模型的泛化准确度造成显著影响。
    layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)),
    #池化层1，2*2采样
    layers.MaxPooling2D((2, 2)),                   
    # 设置二维卷积层2，设置64个3*3卷积核，activation参数将激活函数设置为ReLu函数
    layers.Conv2D(64, (3, 3), activation='relu'),  
    #池化层2，2*2采样
    layers.MaxPooling2D((2, 2)),                   
    
    layers.Flatten(),                    #Flatten层，连接卷积层与全连接层
    layers.Dense(64, activation='relu'), #全连接层，特征进一步提取，64为输出空间的维数，activation参数将激活函数设置为ReLu函数
    layers.Dense(10)                     #输出层，输出预期结果，10为输出空间的维数
])
# 打印网络结构
model.summary()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

该模型有两个主要方面：由卷积层和池化层组成的特征提取前端，以及将进行预测的分类器后端。

对于卷积前端，我们可以从具有小滤波器大小 (3,3) 和适度数量滤波器 (32)的单个卷积层开始，然后是最大池化层。然后可以将过滤器映射展平以向分类器提供特征。

鉴于该问题是一个多类分类任务，我们知道我们将需要一个具有 10 个节点的输出层来预测属于 10 个类中的每一个的图像的概率分布。在特征提取器和输出层之间，我们可以添加一个密集层来解释特征，在这种情况下有64个节点。

所有层都将使用ReLU激活函数。

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d (Conv2D)              (None, 26, 26, 32)        320       
_________________________________________________________________
max_pooling2d (MaxPooling2D) (None, 13, 13, 32)        0         
_________________________________________________________________
conv2d_1 (Conv2D)            (None, 11, 11, 64)        18496     
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 5, 5, 64)          0         
_________________________________________________________________
flatten (Flatten)            (None, 1600)              0         
_________________________________________________________________
dense (Dense)                (None, 64)                102464    
_________________________________________________________________
dense_1 (Dense)              (None, 10)                650       
=================================================================
Total params: 121,930
Trainable params: 121,930
Non-trainable params: 0
_________________________________________________________________
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

五、编译模型

# model.compile()方法用于在配置训练方法时，告知训练时用的优化器、损失函数和准确率评测标准
model.compile(
    # 设置优化器为Adam优化器
    optimizer='adam',
    # 设置损失函数为交叉熵损失函数（tf.keras.losses.SparseCategoricalCrossentropy()）
    # from_logits为True时，会将y_pred转化为概率（用softmax），否则不进行转换，通常情况下用True结果更稳定
    loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
    # 设置性能指标列表，将在模型训练时监控列表中的指标
    metrics=['accuracy'])
1
2
3
4
5
6
7
8
9

六、训练模型

"""
这里设置输入训练数据集（图片及标签）、验证数据集（图片及标签）以及迭代次数epochs
"""
history = model.fit(
    # 输入训练集图片
	train_images, 
	# 输入训练集标签
	train_labels, 
	# 设置10个epoch，每一个epoch都将会把所有的数据输入模型完成一次训练。
	epochs=10, 
	# 设置验证集
    validation_data=(test_images, test_labels))
1
2
3
4
5
6
7
8
9
10
11
12

训练的结果是：

Epoch 1/10
1875/1875 [==============================] - 17s 9ms/step - loss: 0.1390 - accuracy: 0.9569 - val_loss: 0.0479 - val_accuracy: 0.9837
Epoch 2/10
1875/1875 [==============================] - 17s 9ms/step - loss: 0.0457 - accuracy: 0.9863 - val_loss: 0.0454 - val_accuracy: 0.9842
Epoch 3/10
1875/1875 [==============================] - 17s 9ms/step - loss: 0.0320 - accuracy: 0.9899 - val_loss: 0.0303 - val_accuracy: 0.9908
Epoch 4/10
1875/1875 [==============================] - 16s 9ms/step - loss: 0.0231 - accuracy: 0.9924 - val_loss: 0.0292 - val_accuracy: 0.9909
Epoch 5/10
1875/1875 [==============================] - 17s 9ms/step - loss: 0.0181 - accuracy: 0.9942 - val_loss: 0.0267 - val_accuracy: 0.9916
Epoch 6/10
1875/1875 [==============================] - 17s 9ms/step - loss: 0.0129 - accuracy: 0.9959 - val_loss: 0.0281 - val_accuracy: 0.9917
Epoch 7/10
1875/1875 [==============================] - 17s 9ms/step - loss: 0.0113 - accuracy: 0.9966 - val_loss: 0.0362 - val_accuracy: 0.9905
Epoch 8/10
1875/1875 [==============================] - 16s 9ms/step - loss: 0.0090 - accuracy: 0.9970 - val_loss: 0.0332 - val_accuracy: 0.9921
Epoch 9/10
1875/1875 [==============================] - 17s 9ms/step - loss: 0.0074 - accuracy: 0.9975 - val_loss: 0.0382 - val_accuracy: 0.9911
Epoch 10/10
1875/1875 [==============================] - 17s 9ms/step - loss: 0.0070 - accuracy: 0.9976 - val_loss: 0.0361 - val_accuracy: 0.9912
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

我们将为适度的 10 个训练 epoch 训练基线模型，默认批量大小为 32 个示例。每个折叠的测试集将用于在训练运行的每个时期评估模型，以便我们以后可以创建学习曲线，并在运行结束时，以便我们可以估计模型的性能。因此，我们将跟踪每次运行的结果历史记录，以及折叠的分类准确性。

scores, histories = list(), list()
_, acc = model.evaluate(test_images, test_labels, verbose=0)
scores.append(acc)
histories.append(history)
1
2
3
4

七、模型预测

通过上面的网络结构我们可以简单理解为，输入一张图片，将会得到一组数，这组代表这张图片上的数字为0~9中每一个数字的几率（并非概率），out数字越大可能性越大。

plt.imshow(test_images[1].reshape(28,28))
1

我们输出测试集中第一张图片的预测结果：

pre = model.predict(test_images) # 对所有测试图片进行预测
pre[1] # 输出第一张图片的预测结果
1
2

它运行的结果是：

array([-9.2362501e-03,  7.8086529e+00,  2.3511787e+01, -1.7476982e+01,
        1.8420624e+00, -1.9809229e+01,  4.6623755e+00, -1.0565450e+01,
       -5.0866108e+00, -4.9108720e+00], dtype=float32)
1
2
3

八、模型评估

我们试着创建一个带有两个子图的单个图形，一个用于损失，一个用于准确性。蓝线将表示模型在训练数据集上的性能，橙色线将表示在保留测试数据集上的性能。

for i in range(len(histories)):
    # plot loss
    plt.subplot(2, 1, 1)
    plt.title('Cross Entropy Loss')
    plt.plot(histories[i].history['loss'], color='blue', label='train')
    plt.plot(histories[i].history['val_loss'], color='orange', label='test')
    # plot accuracy
    plt.subplot(2, 1, 2)
    plt.title('Classification Accuracy')
    plt.plot(histories[i].history['accuracy'], color='blue', label='train')
    plt.plot(histories[i].history['val_accuracy'], color='orange', label='test')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12

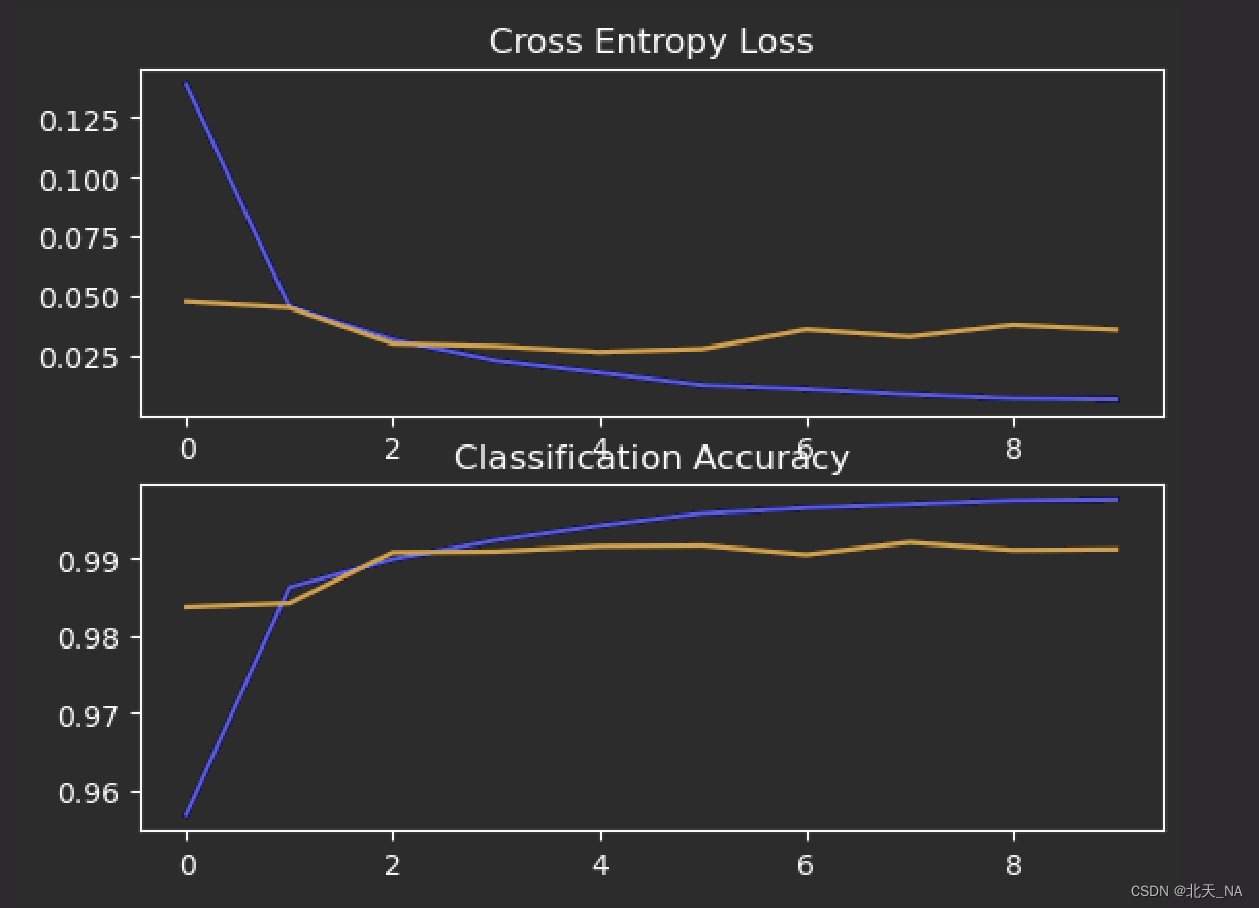
在这种情况下，我们可以看到模型通常实现了良好的拟合，训练和测试学习曲线收敛。没有明显的过拟合或欠拟合迹象。

九、最后我想说

本周的任务就到这里完成了，这个模型可能不是最好的模型，后续你们也可以进行模型的改进，可以多探索学习算法的许多方面的改进，也可以尝试将模型深度进行增加然后训练看看。

另外想说的是，我的后续博客的方面会更加偏向于基础知识、数据结构以及算法的总结，其他方面的我就会更新的比较慢，见谅。

还有一点，有人可能想知道学习了这么久的深度学习是什么？我简单的说一下，深度学习是机器学习的一个分支。许多传统机器学习算法学习能力有限，数据量的增加并不能持续增加学到的知识总量，而深度学习系统可以通过访问更多数据来提升性能，即“更多经验”的机器代名词。机器通过深度学习获得足够经验后，即可用于特定的任务，如驾驶汽车、识别田地作物间的杂草、确诊疾病、检测机器故障等。

最后，谢谢认真阅读完的朋友，你们可以在自己的电脑上进行尝试，也希望你们能从这个过程中学到知识，谢谢！