详解时间复杂度计算公式(附例题细致讲解过程)

这几天开始刷力扣上面的算法题，有些题目上面限制时间复杂度和空间复杂度，题目虽然写出来了，但是很没底。印象里数据结构老师讲过一点，沉睡的记忆苏醒了。只记得一个时间复杂度是O(n)，空间复杂度是S(n)。for循环常常是O(n)，具体是怎么算的不清楚。所以在看了相关的视频教学后，总结一下时间复杂度的计算公式，希望能给大家的学习带来帮助!

目录

一、什么是时间复杂度 

二、单层循环时间复杂度计算公式

三、两层循环时间复杂度计算公式

四、多层循环时间复杂度计算公式

方法一：抽象为计算三维物体体积

方法二：列式求和

---

一、什么是时间复杂度 

时间复杂度（Time complexity）是一个函数，它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数. 时间复杂度常用大O表述，不包括这个函数的低阶项和首项系数。

时间复杂度大小比较：

时间复杂度分类：

• 算法完成工作最少需要多少基本操作叫做最优时间复杂度，是一种最乐观最理想的状态。
• 算法完成工作最多需要多少基本操作叫做最坏时间复杂度，是算法的一个保障。
• 算法完成工作平均需要多少基本操作叫做平均时间复杂度，它可以均匀全面的评价一个算法的好坏。

时间复杂度基本计算规则：

1. 基本操作即只有常数项，认为其时间复杂度为O(1)
2. 顺序结构，时间复杂度按加法进行计算
3. 循环结构，时间复杂度按乘法进行计算
4. 分支结构，时间复杂度取最大值
5. 判断一个算法效率时，往往只需要关注操作数量的最高次项，其他次要项和常数项可以忽略
6. 在没有特殊说明时，我们所分析的时间复杂度都是指最坏时间复杂度

二、单层循环时间复杂度计算公式

 解题步骤

1. 列出循环趟数t及每轮循环i的变化值
2. 找到t与i的关系
3. 确定循环停止条件
4. 联立两式解方程
5. 写结果

 例题分析

 例一：

i = n*n;
whlie(i != 1)
    i = i/2;

第一步：列出循环趟数t及每轮循环i的变化值：

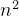
第二步：找到t与i的关系：

 

第三步：确定循环停止条件：

第四步：联立第二步第三步两式解方程：

所以得到时间复杂度为：

例二:

x = 0；
while (n>=(x+1)*(x+1))
    x = x+1;

第一步：列出循环趟数t及每轮循环x的变化值：

第二步：找到t与x的关系：

 

第三步：确定循环停止条件：

第四步：联立第二步第三步两式解方程：

所以得到时间复杂度为：

 例三:

int i = 1;
while (i<=n)
    i = i *2

第一步：列出循环趟数t及每轮循环i的变化值：

第二步：找到t与x的关系：

 

第三步：确定循环停止条件：

第四步：联立第二步第三步两式解方程：

所以得到时间复杂度为：

 例四:

int i = 0;
while (i*i*i<=n)
    i ++;

第一步：列出循环趟数t及每轮循环i的变化值：

第二步：找到t与x的关系：

 

第三步：确定循环停止条件：

第四步：联立第二步第三步两式解方程：

所以得到时间复杂度为：

 例五:

y = 0;
while (y+1)*(y+1) <= n
    y = y+1;

第一步：列出循环趟数t及每轮循环y的变化值：

第二步：找到t与x的关系：

 

第三步：确定循环停止条件：

第四步：联立第二步第三步两式解方程：

所以得到时间复杂度为：

三、两层循环时间复杂度计算公式

 解题步骤

1. 列出循环中i的变化值
2. 列出内层语句的执行次数
3. 求和，写结果

 例题分析

例一:

int m=0,i,j;
for (i=1;i<=n;i++)
    for(j=1;j<=2*i;j++)
        m++;

第一步列出循环中i的变化值：

第二步列出内层语句的执行次数：

第三步 求和，写结果

 例二:

for (i=0;i
    for(j=0;j
        a[i][j] = 0;

第一步列出循环中i的变化值：

第二步列出内层语句的执行次数：

第三步 求和，写结果

 例三:

count = 0;
for (k=1;k<=n;k*=2)
    for(j=1;j<=n;j++)
        count ++;

这里k*=2，不再是++,所以要先用单层循环求出变换趟数：

内层每个都是n,求和则可以得到：

 例四:

for (i=n-1;i>=1;i--)
    for(j=1;j<=i;j++)
        if A[j] > A [j+1]
            A[j]与A[j+1]交换;

第一步列出循环中i的变化值：

第二步列出内层语句的执行次数：

第三步 求和，写结果

四、多层循环时间复杂度计算公式

方法一：抽象为计算三维物体体积

方法二：列式求和

例一:

for(i=0;i<=n;i++)
    for(j=0;j<=i;j++)
        for(k=0;k

方法一：抽象为计算三维物体体积：

 i依赖于n，j依赖于i，k依赖于j，三者都可以看成是n，再由体积公式可以求出

。

方法二：列式求和：

∑i=0n∑j=0i∑k=0j−1=∑i=0n∑j=0i\(j−1−0+1)=∑i=0n∑j=0i\j" role="presentation">∑ni=0∑ij=0∑j−1k=0=∑ni=0∑ij=0\(j−1−0+1)=∑ni=0∑ij=0\j$\sum _{i=0}^n\sum _{j=0}^i\sum _{k=0}^{j-1}=\sum _{i=0}^n\sum _{j=0}^i\text{(}j-1-0+1)=\sum _{i=0}^n\sum _{j=0}^i\text{j}$