【C++】栈~~（很详细哦）

在前几天，我们刚一起学过顺序表，链表（无头单向不循环，有头双向循环），这两种都属于线性表因为是一系列存储的。而以后的哈希表则是散列表

今天我们看一下栈

目录

1.栈的介绍

2.实现

3.题目 

---

1.栈的介绍

栈，又叫做栈帧，也是一种数据结构（和顺序表链表一样），但是他自己的结构也有一些特殊的地方

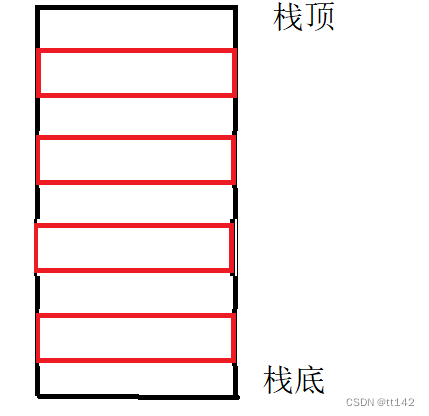
 他是这样的，我们把底部叫做栈底，顶部叫做栈顶，通俗易懂对吧，但是他有一个小规则，只能从栈顶存储或者销毁数据，如果现在有一个空栈，那么存储删除数据就是下面这样的 

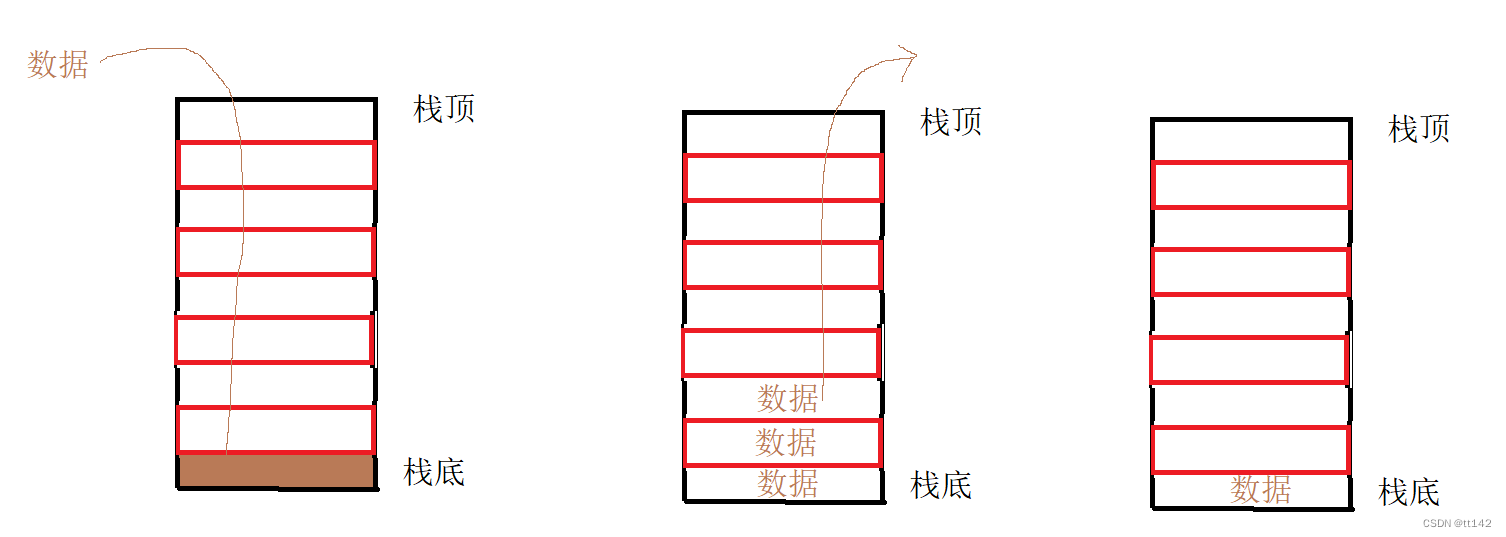
 永远不可能从栈底拿出数据，没有为什么~~

或者你也可以总结成LIFO原则（last in first out）即后进先出

2.实现

不难发现，其实他的结构和之前学过的顺序表 链表很相似，我们已经写过两个了，这个可不可以仿照着写呢？那模仿哪一个更好？

分析一下啦

首先他不存在不连续存储的问题，在这点上其实二者（顺序表，链表）都行，但是既然都连续存储了还是顺序表更方便一下，不需要指针指来指去

其次最好可以很方便的访问数据，而且能快速进行一个位置（栈顶或者栈底）的增删，因为栈的结构就决定他只需要一个位置增删就可以，那就是顺序表的下标访问最合适不过了~~~

所以我们采取顺序表的写法来写栈

对于顺序表不了解的同学赶紧去看看我的顺序表那篇文章在下面

顺序表在这里

 头文件

#pragma once
#include 
#include 
#include 
#include 
typedef int type;
typedef struct Stack
{
	type *a;
	int top;// 初始化成0 表示栈顶位置下一个位置的下标
	int capacity;
}ST;
 
void InitST(ST* p);//初始化
void PushST(ST* p,type x);//在栈顶压数据
void PopST(ST* p);//从栈顶删除数据
void DestoryST(ST* p);//销毁栈
bool Empty(ST* p);//判断栈是不是空
type StackTop(ST* p);//显示栈顶的数据
type SizeST(ST* p);//栈里面数据的个数

实现

#include "stack.h"
 
void InitST(ST* p)//初始化
{
	type* tmp = (type*)malloc(sizeof(type)*4);
	if (tmp == NULL)
	{
		perror("InitST");
		exit(-1);
	}
	p->a = tmp;
	p->capacity = 4;
	p->top = 0;
}
 
void PushST(ST* p, type x)//在栈顶压数据
{
	if (p->capacity == p->top)//表示需要扩容
	{
		ST* tmp = (ST*)realloc(p->a, p->capacity* 2*sizeof(type));
		if (tmp == NULL)
		{
			perror("realloc");
			exit(-1);
		}
		p->a = tmp;
		p->capacity *= 2;
	}
	p->a[p->top] = x;
	p->top++;
}
 
void PopST(ST* p)//从栈顶删除数据
{
	assert(p);
	assert(!Empty(p));
	p->top--;
}
 
void DestoryST(ST* p)//销毁栈
{
	assert(p);
	free(p->a);
	p->a = NULL;
	p->capacity = p->top = 0;
}
 
bool Empty(ST* p)//判断栈是不是空
{
	assert(p);
	return p->top == 0;
}
 
type StackTop(ST* p)//显示栈顶的数据
{
	assert(p);
	assert(!Empty(p));
	return p->a[p->top - 1];
}
 
type SizeST(ST* p)//栈里面数据的个数
{
	assert(p);
	return p->top;
}

3.题目

有效括号（典中典）

题目在这里大家先自己做一下

我们用C语言写一下，其实就是匹配的问题，如果都是左括号比如（，{，【，这些都是要压栈的，不需要遍历到结束再去判断是否匹配的问题，只要遇到右括号就及时匹配就好了

因为是C语言写的所以需要在前面把我们写的栈带上

typedef int type;
 
typedef struct Stack
{
	type *a;
	int top;// 初始化成0 表示栈顶位置下一个位置的下标
	int capacity;
}ST;
bool Empty(ST* p)//判断栈是不是空
{
	assert(p);
	return p->top == 0;
}
void InitST(ST* p)
{
	type* tmp = (type*)malloc(sizeof(type)*4);
	if (tmp == NULL)
	{
		perror("InitST");
		exit(-1);
	}
	p->a = tmp;
	p->capacity = 4;
	p->top = 0;
}
 
void PushST(ST* p, type x)//在栈顶压数据
{
	if (p->capacity == p->top)//表示需要扩容
	{
		type* tmp = (type*)realloc(p->a, p->capacity* 2*sizeof(type));
		if (tmp == NULL)
		{
			perror("realloc");
			exit(-1);
		}
		p->a = tmp;
		p->capacity *= 2;
	}
	p->a[p->top] = x;
	p->top++;
}
 
void PopST(ST* p)//从栈顶删除数据
{
	assert(p);
	assert(!Empty(p));
	p->top--;
}
 
void DestoryST(ST* p)//销毁栈
{
	assert(p);
	free(p->a);
	p->a = NULL;
	p->capacity = p->top = 0;
}
 
type StackTop(ST* p)//显示栈顶的数据
{
	assert(p);
	assert(!Empty(p));
	return p->a[p->top - 1];
}
 
bool isValid(char * s){
ST st;
InitST(&st);
while(*s)
{
    if(*s=='(' || *s=='[' || *s=='{')
    {
        PushST(&st,*s);
        ++s;
    }
    else
    {
        if(Empty(&st))
        {
            DestoryST(&st);
             return false;
 
        }
        char top=StackTop(&st);
          PopST(&st);
          if((*s==')'&& top!='(' )||(*s==']'&& top!='[' )||( *s=='}'&&top!='{'))
          {
            DestoryST(&st);
             return false;
          }
             else{
                 s++;
             }
          
    }
   
}
 bool ret=Empty(&st);
            DestoryST(&st);
     return ret;
}

---

大家学会了吗~~~