线性递推数列的通项公式（非常简单，三步完成）

获取线性递推数列通项的方法有很多（参考百度百科：斐波那契数列），这里简单介绍一种容易理解的方法：待定系数法构造等比数列求特征方程，最终求得通项公式。

证明过程理解即可，实际计算起来非常简单的。

理论推导：

通常我们得到的递推数列是这样的形式：

目标是求的通项公式。

首先，上面的递推数列通常可以写成下面这种形式：

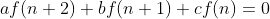      ---------------------（式1）

也叫二阶差分式（或者叫递推式）。

为了求出一阶差分式，我们可以将原式写成如下形式：

其中，因此上式就是以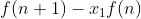为元素的等比数列，公比为。

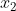通过移项同时可得:

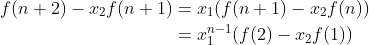
与上面的式子完全等价。

两式子相减则有：

 因此通项公式就求出来了：

现在需要解出x1,x2：
利用二次方程根与系数的关系，可知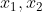恰为方程的两根，注意这里的系数abc就是上面二阶差分式（式1）的系数，不用计算，可以直接拿来用。该二次方程就是原差分方程的特征方程。

 求方程的根解除x1，x2后带入通项公式即可得到f(n)的表达式。

实际做题的计算步骤（更简单）：

1.移项写出二阶差分式，得到系数abc，也就获得了二次方程的系数abc。

2.解出二次方程的两个根x1，x2。

3.带入f(n)的通项公式即可。

例子：

斐波那契数列，它满足,

首先写出移项到左边的二阶差分式的标准形式：，获得系数abc分别为1，-1，-1，那么差分式的特征方程就为，解得

带入通用的通项公式即可得到f(n)的通项公式：

完。

另外需要注意：该通项公式仅适用于线性的递推数列！