引言

上一节介绍了规划与学习的相关信息，并介绍了直接强化学习(Direct Reinforcement Learning)和间接强化学习(Indirect Reinforcement Learning),本节利用上述两种概念，介绍$Q$规划算法与Dyna-Q算法。

回顾：直接强化学习与间接强化学习

如果单纯使用规划方法，其主要思想表示如下：

• 已知环境模型——对任意状态$s\in \mathcal{S}$，动作$a\in \mathcal{A}(s)$确定的情况下，其转移后的新状态$s^{\prime }$，对应的奖励结果$r$的动态特性函数$P(s^{\prime },r\mid s,a)$均是给定的；
• 根据状态-动作对$(s,a)$，通过 环境模型 进行搜索(Search)，得到新状态$s^{\prime }$和对应奖励结果$r$(基于 模拟经验(Simulation Experience)产生的结果);
  注意：此时产生的s'和r被称为‘模拟经验’——它并不是从真实环境中真实地执行了一次状态转移过程，而是在动态特性函数P(s',r|s,a)中基于转移后新状态的概率分布，随机选择的结果。
• 至此，得到了一组 模拟状态转移结果 $\to (s,a,s^{\prime },r)$，利用该结果更新策略$\pi$。
  以动态规划方法为例，该方法主要使用策略迭代操作：
  • 策略评估(Policy Evaluation)：(贝尔曼期望方程的不动点性质)
    $$V_{k+1}(s)=\sum _{a\in \mathcal{A}(s)}\pi (a\mid s)\sum _{s^{\prime },r}P(s^{\prime },r\mid s,a)[r+\gamma V_k(s^{\prime })]$$
  • 策略改进(Policy Improvment)：(贪心算法)
    π ∗ ( a ∣ s ) = { 1 i f a = arg ⁡ max ⁡ a ∈ A q π ∗ ( s , a ) 0 e l s e \pi_*(a \mid s) = \left\{
    1ifa=arg⁡maxa∈A⁡qπ∗(s,a)0else" role="presentation" style="position: relative;">1ifa=argmaxa∈Aqπ∗(s,a)0else$$\begin{array}{l}1ifa=\underset{a\in \mathcal{A}}{\arg max}{q}_{{\pi }^{\ast }}(s,a)\\ 0else\end{array}$$
    \right. π∗​(a∣s)={1ifa=a∈Aargmax​qπ∗​(s,a)0else​

由于上述思想是基于环境模型给定的条件下，直接使用环境模型对策略进行规划。因此，上述方法属于直接强化学习。
直接强化学习的定义：在真实环境中采集真实经验，根据真实经验直接更新值函数或策略，不受模型偏差的影响。
在动态规划方法中，它通过动态特性函数获取模拟经验，它不是真实经验，但为什么‘动态规划方法’是‘直接强化学习’呢？
以下是个人看法：动态规划中已知的动态特性函数就是‘理想状态下模型的表达’——也可以理解成经过无数次采样近似出的‘完美环境模型’。因此，动态规划方法产生的经验同样是‘真实经验’。

使用学习方法的主要思想是基于环境模型未知或未完全可知，导致我们 无法使用环境模型直接对策略进行规划。因此，使用学习(Learning)方法求解真实经验：

在真实环境中，给定状态$s$条件下，选择具体动作$a\in \mathcal{A}(s)$，并执行一次真实的状态转移过程得到新状态$s^{\prime }$以及对应奖励$r$。至此，我们得到一组 真实状态转移结果$(s,a,s^{\prime },r)$，在求解策略$\pi$的方向中，共分为 两条路径：

• 由于$(s,a,s^{\prime },r)$是真实转移结果，完全可以 使用采样近似的方法直接求解策略$\pi$。例如$Q-Learning$：
  • 评估过程：
    $$Q(s,a)\leftarrow Q(s,a)+\alpha [r+\gamma \underset{a}{\max }Q(s^{\prime },a)-Q(s,a)]$$
  • 改进过程($ϵ-$贪心策略)：
    a ∗ ← arg ⁡ max ⁡ a Q ( s , a ) b ( a ∣ s ) ← { 1 − ϵ k + ϵ k ∣ A ( s ) ∣ i f a = a ∗ ϵ k ∣ A ( s ) ∣ o t h e r w i s e
    a∗←arg⁡maxa⁡Q(s,a)b(a∣s)←{1−ϵk+ϵk|A(s)|ifa=a∗ϵk|A(s)|otherwise" role="presentation" style="position: relative;">a∗b(a∣s)←argmaxaQ(s,a)←{1−ϵk+ϵk|A(s)|ifa=a∗ϵk|A(s)|otherwise$$\begin{array}{rl}{a}^{\ast }& \leftarrow \underset{a}{\arg max}Q(s,a)\\ b(a\mid s)& \leftarrow \{\begin{array}{l}1-{ϵ}_k+\frac{{ϵ}_k}{|\mathcal{A}(s)|}ifa=a^{\ast }\\ \frac{{ϵ}_k}{|\mathcal{A}(s)|}otherwise\end{array}\end{array}$$
    a∗b(a∣s)​←aargmax​Q(s,a)←{1−ϵk​+∣A(s)∣ϵk​​ifa=a∗∣A(s)∣ϵk​​otherwise​​

这种方法通过真实采样直接对策略$\pi$进行学习。因此，上述方式同样属于直接强化学习。

• 另一条路线：使用真实转移结果去近似求解模型(这里区别于上述给定的环境模型)，此时已经有了模型，完全可以再次使用规划方法对策略进行求解。

这种方式明显是先求模型，再通过模型求解策略——我们称其为间接强化学习。

规划与学习的差异性

分布模型与样本模型

• 在理想情况下，例如动态规划方法，我们无须担心环境模型，该模型是一个 完全符合环境的、完美的概率分布——我们称该模型为分布模型；
• 在真实环境中，上面的分布模型是极难实现的，我们只能通过真实样本作为输入，通过 真实的状态转移过程 得到真实经验，从而对模型进行学习。
  但这种做法会带来模型偏差：通过真实样本结果得到了一个状态转移后的新状态，但 真实情况可能是新状态的选择存在随机性。即它有可能选择好多种状态，该真实样本只是恰巧选择了其中一个。
  在这里我们为简化起见：消除随机性，将 真实样本直接看成环境模型。即不考虑任何模型偏差，将真实样本$(s,a,s^{\prime },r)$视作$P(s^{\prime },r\mid s,a)=1$的环境模型。它的概率分布可以理解为：
  P ( s ′ , r ∣ s , a ) ← { 1 i f S t + 1 = s ′ , R t + 1 = r 0 o t h e r w i s e P(s',r \mid s,a) \gets \left\{
  1ifSt+1=s′,Rt+1=r0otherwise" role="presentation" style="position: relative;">1ifSt+1=s′,Rt+1=r0otherwise$$\begin{array}{l}1if{S}_{t+1}=s^{\prime },R_{t+1}=r\\ 0otherwise\end{array}$$
  \right. P(s′,r∣s,a)←{1ifSt+1​=s′,Rt+1​=r0otherwise​
  我们称该模型为样本模型。

从算法更新图的角度认识规划与学习的差异性

观察动态规划方法、蒙特卡洛方法、时序差分方法的算法更新图如下：

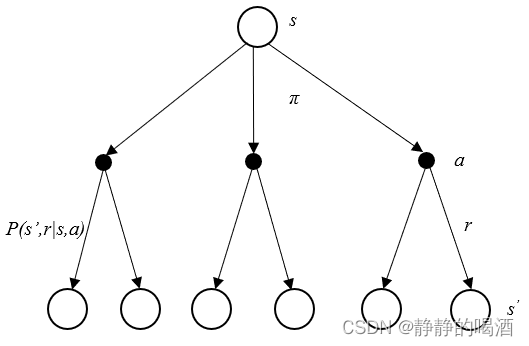
三张图中，只有动态规划方法是基于规划方法执行的操作，剩余两种方法是基于学习方法执行的操作。观察：

• 动态规划方法将 一次状态转移后的所有可能发生的新状态全部遍历一遍，并对所有新状态的价值函数进行求解，最终使用所有状态价值函数的期望对当前状态进行更新。我们称这种更新方式为 期望更新。
  $$V_{k+1}(s)=\sum _{a\in \mathcal{A}(s)}\pi (a\mid s)\sum _{s^{\prime },r}P(s^{\prime },r\mid s,a)[r+\gamma V_k(s^{\prime })]$$
• 反观蒙特卡洛、时序差分方法，他们都是通过采集真实样本对当前状态进行更新。我们称这种更新方式为 采样更新。

从遍历深度和遍历广度两个角度观察规划和学习的差异性：

• 从广度角度(执行一次状态转移操作后遍历新状态的数量)来看，基于学习方法的采样更新自然 一次只能遍历一个新状态节点，基于规划方法的期望更新能够 一次遍历多个新状态节点；
  采样不广

• 从深度角度(更新一次策略需要的状态转移次数)来看，时序差分方法、动态规划方法都基于 自举(Bootstrapping)思想，因此每次迭代仅执行一次状态转移过程；
  即便是SARSA,使用同轨策略执行了两次动作的选择，但仍然是只有一次状态转移过程。
  但蒙特卡洛方法至少要遍历一个完整情节才能执行一次迭代过程，一个完整情节的遍历自然存在若干次状态转移过程。
  自举不深

随机采样单步表格式Q规划

该算法的算法流程表示如下：

• 从状态集合$\mathcal{S}$中随机选择某一状态$s\in \mathcal{S}$，从对应的动作集合$\mathcal{A}(s)$中选择一个动作$a\in \mathcal{A}(s)$构成状态-动作对$(s,a)$；
• 将状态-动作对$(s,a)$带入样本模型(Sample Model)，从而得到下一时刻状态$s^{\prime }$和对应奖励$r$；
  该步骤体现的Planning思想;
• 将该样本$(s,a,s^{\prime },r)$使用$Q-Planning$进行对$Q-Table$进行更新；
  该步骤体现的Q-Learning思想;
  $$Q(s,a)\leftarrow Q(s,a)+\alpha [r+\gamma \underset{a}{\max }Q(s^{\prime },a)-Q(s,a)]$$

本质上Q规划是将规划(Planning)和Q-Learning相结合的简单算法。
分析：该算法中的样本模型(Sample Model)是 给定 的(在算法执行之前，就已经通过真实样本构建了一个样本模型)
这种模型即：给定一个状态$s\in \mathcal{S}$，某一动作$a\in \mathcal{A}(s)$，必然会转移至确定状态$s^{\prime }$ 及对应奖励结果$r$。
通过观察可知，Q-规划算法中并不存在通过真实样本去学习环境模型的步骤，自然也不存在环境模型被更新的过程。
其本质上就是构建了一个 当前样本模型相匹配的$Q-Table$而已。

Dyna-Q算法

初始化部分：
状态集合：$\mathcal{S}$；动作集合：$s\in \mathcal{S},a\in \mathcal{A}(s)$；$Q-Table$：$Q(s,a)\in \mathbb{R}$；样本模型(Sample Model)：$Model(s,a)\in \mathbb{R}$
注意：这里以‘样本模型’为例。
该算法的算法流程可以表示为两个过程：
学习过程：

• repeat 每个情节$k=0,1,2,...$；
• 当前状态(非终止状态)$s$；
• 从基于$Q-Table$中 状态$s$ 所在行使用$ϵ-$贪心策略$\pi (s)$随机获取动作$a$；
  a ∗ ← arg ⁡ max ⁡ a Q ( s , a ) π ( s ) ← { 1 − ϵ k + ϵ k ∣ A ( s ) ∣ i f a = a ∗ ϵ k ∣ A ( s ) ∣ o t h e r w i s e a ← π ( s )
  a∗←arg⁡maxa⁡Q(s,a)π(s)←{1−ϵk+ϵk|A(s)|ifa=a∗ϵk|A(s)|otherwisea←π(s)" role="presentation" style="position: relative;">a∗π(s)a←argmaxaQ(s,a)←{1−ϵk+ϵk|A(s)|ifa=a∗ϵk|A(s)|otherwise←π(s)$$\begin{array}{rl}{a}^{\ast }& \leftarrow \underset{a}{\arg max}Q(s,a)\\ \pi (s)& \leftarrow \{\begin{array}{l}1-{ϵ}_k+\frac{{ϵ}_k}{|\mathcal{A}(s)|}ifa=a^{\ast }\\ \frac{{ϵ}_k}{|\mathcal{A}(s)|}otherwise\end{array}\\ a& \leftarrow \pi (s)\end{array}$$
  a∗π(s)a​←aargmax​Q(s,a)←{1−ϵk​+∣A(s)∣ϵk​​ifa=a∗∣A(s)∣ϵk​​otherwise​←π(s)​
• 执行动作$a$,得到下一状态$s^{\prime }$和对应奖励$r$;
• 根据上述状态转移过程对$Q-Table$进行更新；
  $$Q(s,a)\leftarrow Q(s,a)+\alpha [r+\gamma \underset{a}{\max }Q(s^{\prime },a)-Q(s,a)]$$
• 将转移后的结果$s^{\prime },r$添加到$Model$中(s,a)对应位置上；
  $$Model(s,a)\leftarrow s^{\prime },r$$
• 规划过程(嵌套循环)：

规划过程：

• repeat $n$次($n$表示规划次数)；
• 从被访问过的状态集合中随机选择一个状态$\hat{s}$；
• 从被访问过的动作集合中随机选择一个动作$\hat{a}$；
• 将$s,a$带入，通过模型$Model$得到一个 模拟经验结果(状态转移结果)$\widehat{s^{\prime }},\hat{r}$；
• 将上述状态转移过程对$Q-Table$进行更新；
• $$Q(\hat{s},\hat{a})\leftarrow Q(\hat{s},\hat{a})+\alpha [\hat{r}+\gamma \underset{a}{\max }Q(\widehat{s^{\prime }},a)-Q(\hat{s},\hat{a})]$$

分析：

• 如果$n=0$，整个算法将退化为$Q-Learning\to$只能通过当前情节每状态转移一次就更新一次$Q-Table$；
• $n>0$条件下发现，学习过程和规划过程都在更新同一个$Q-Table$，并且每次迭代(学习过程中的一次状态转移过程) $Q-Table$更新次数 $<=n+1$；
  原因在于，如果在规划过程抽取出的‘状态-动作对’$(\hat{s},\hat{a})$中的$\hat{a}\notin \mathcal{A}(\hat{s})$,此时$Model$中也不存在相应记录，也不会返回对应的$\widehat{s^{\prime }},\hat{r}$,相当于一个‘空循环’——没有更新Q-Table中的任何信息。

下一节将介绍基于Dyna-Q在算力聚焦思想中的改进——Dyna-Q+算法。

相关参考：
【强化学习】规划与学习-Dyna Architecture
深度强化学习原理、算法与PyTorch实战——刘全、黄志刚编著