Java实现二叉树两个节点最近公共祖先

Java：二叉树的最近公共祖先

前言

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”
来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree

一、示例

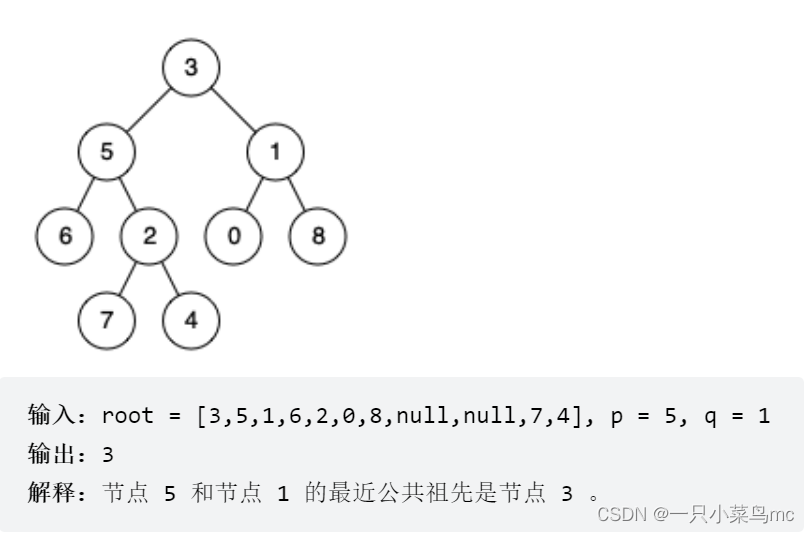
二、解题思路

1.p、q可能出现的位置

p、q存在的三种情况
（1）p、q其中一个为root节点 则root为公共祖先。

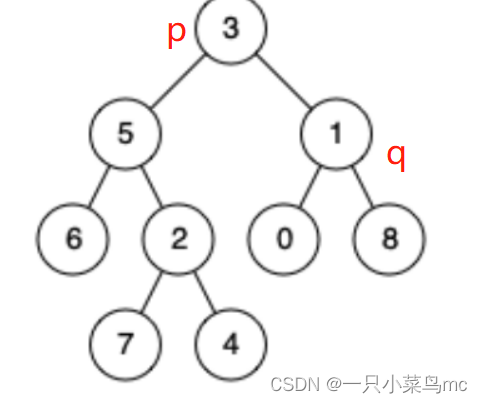
（2）p、q在根节点的左右两边

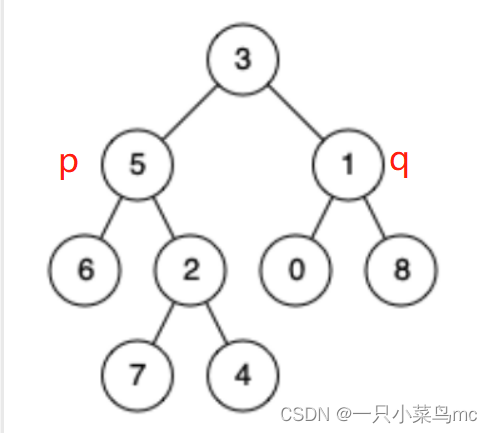
（3）p、q在根节点的左边或者右边

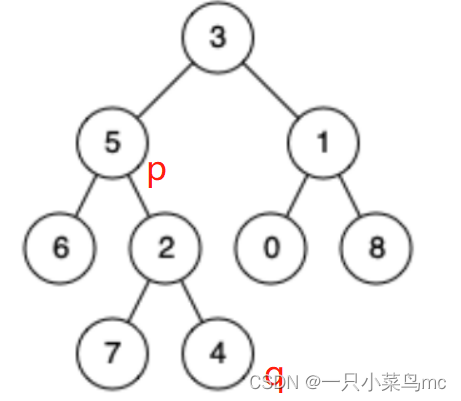
代码如下（示例）：

class Solution {
    
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root==null){
            return null;
        }
        if(q==root||p==root){
            return root;//递归推出条件：根是祖先，根不是祖先在左子树和右子树找祖先。
        }
        TreeNode retLeft = lowestCommonAncestor(root.left,p,q);
        TreeNode rightret = lowestCommonAncestor(root.right,p,q);
        //第一个if ：p 和q 再root的两边。第二个分支：pq的在根的左侧
        //最后一种情况：qp在根的右侧
        if(retLeft!=null&&rightret!=null){
            return root;
        }else if(retLeft!=null&&rightret ==null){
            return retLeft;
        }else{
            return rightret;
        }
    }
}

2.假设二叉树的表示方法为双亲表示法

	这样可以根据双亲节点求q 的p深度，假设q的深度为qlen ，p的长度为plen，然后让深度大节点向根节点先走abs（qlen-plen）步，然后同时走，当p\q两个节点相遇则会找到最近的公共祖先。
	但是题目中是孩子表示法，我们可以参照双亲表示法，求q、q的深度，可以通过遍历q、p，将其路径保存到2个栈中求P、q 的深度。栈的大小就是深度。
	然后让栈大的栈先出差值个元素
	然后同时出栈顶的元素，当2个栈的栈顶元素相同，则为最近的公共祖先。

代码如下：

if(root==null){
            return null;
        }
        if(root==q||root==p){
            return root;
        }
        Stack<TreeNode> stackq = new Stack<>();
        Stack<TreeNode> stackp = new Stack<>();
        TreeNode cur1 = root;
        TreeNode cur2 = root;
        Path(cur1,stackq, q);
        Path(cur2,stackp,p);
        int size1 = stackp.size();
        int size2 = stackq.size();
        if(size1>size2){
       //判断栈的大小
            int size = size1-size2;
            while(size!=0){
                stackp.pop();//大的栈先出差值个元素
                size--;
            }
            while(!stackp.isEmpty()&&!stackq.isEmpty()){
                if(stackp.peek()==stackq.peek()){//两个栈同时出，值相等则为公共祖先。
                    return stackp.peek();
                }else{
                    stackp.pop();
                    stackq.pop();
                }
            }
        }else{
            int size = size2-size1;
            while(size!=0){
                stackq.pop();
                size--;
            }
            while(!stackp.isEmpty()&&!stackq.isEmpty()){
                if(stackp.peek()==stackq.peek()){
                    return stackp.peek();
                }else{
                    stackp.pop();
                    stackq.pop();
                }
            }
       return null;
     }
    public boolean Path(TreeNode root,Stack<TreeNode> stack, TreeNode q){
    //递归寻找节点的路径。
        if(root == null||q==null){
            return false;
        }
        //根节点入栈
        stack.push(root);
        if(root == q){
            return true;//递归退出条件.找到了节点的位置
        }
        boolean leftNode = Path(root.left,stack,q);//根不等于节点，在根的左树找
        if(leftNode){
           return true;
        }
        leftNode = Path(root.right,stack,q);//根不等于节点，在根的右树找
        if(leftNode){
           return true;
        }
        stack.pop();//左右都没找到，需要出当前根（栈顶）的值
        return false;


        

    }

总结