实用拜占庭协议（PBFT 99）

文献：

1. 拜占庭容错：Lamport L, Shostak R, Pease M. The Byzantine generals problem[M]//Concurrency: the works of leslie lamport. 2019: 203-226.
2. 实用拜占庭容错：Castro Miguel and Barbara Liskov. “Practical byzantine fault tolerance.” OsDI. Vol. 99. No. 1999. 1999.

PBFT（1999）

Lamport 提出了第一个拜占庭容错协议，但是它工作在可信的同步信道上，且复杂度随节点个数增长而指数级增加。它主要是理论意义上的可行性证明，但并不实用。

1999年，Liskov 等人提出了 Practical byzantine fault tolerance，利用了Hash函数、数字签名算法、消息验证码，它是第一个工作在异步网络上的拜占庭容错协议，且复杂度只有$O(n^2)$

因为工作在存在恶意敌手的异步网络上，因此一个节点在一轮通信中可以有三种动作：

1. 有响应，并且是正确的结果，它可能来自诚实节点，但也可能来自恶意节点。
2. 无响应，可能是因为网络延迟和节点故障，也可能是敌手恶意延迟。
3. 有响应，但是恶意节点发送了错误的结果。故障节点也可能发送错误信息，但随机错误无法通过签名验证，可视为无响应。

假设算法可以最多容忍$f$个恶意节点，总的节点数为$n$。某个节点接收其他节点的消息时，某些节点无响应，且响应的节点中包含错误信息；最坏情况下，存在$f$个恶意节点，存在$f$个无响应节点，并且两者不重合；此时，节点收到了$n-f$个消息（包括自己），其中$f$条消息不可信；为了利用少数服从多数规则得到正确结果，要保证正确节点的消息是大多数，即$n-2f>f$，那么需要
$$n\ge 3f+1$$
PBFT 是一种状态机复制算法（a form of state machine replication），每个状态机都维护服务状态并实现服务操作。令$R$是这些副本（replicas）的集合，大小为$n=3f+1$，其中一个副本叫做 primary，其他副本叫做 backups。为了保持分布式系统的活性（liveness），副本在视图（view）中移动。在视图$v$中，primary 是第 $p=v\mathrm{mod}n$ 号机器，其他的机器是 backup。

工作流程如下：

1. client 利用点对点信道发送请求给 primary，形式为
   { R E Q U E S T , o p , t , c } : c \{REQUEST,op,t,c\}:c {REQUEST,op,t,c}:c
   这里$op$是读写指令，$t$是时间戳（timestamp，用于实现 exactly-once semantic），$c$是客户ID，符号“$:c$”表示附加上$c$的签名。

2. primary 把得到的请求广播给所有的 backups

3. 每个 replicas 执行请求，把结果发送给 client，形式为
   { R E P L Y , v , t , c , i , r } : i \{REPLY,v,t,c,i,r\}:i {REPLY,v,t,c,i,r}:i
   这里$v$是当前视图的编号，$i$是副本ID，$r$是计算结果。

4. client 等待$f+1$个来自不同 replicas 的验签通过的相同结果$(t,r)$，那么其中一定有至少$1$个是诚实副本的结果，接受它。

5. 设置计时器，如果没能等到足够的相同结果，那么就利用广播信道给所有的 replicas 重发请求，并回到 step 4

   1. 如果 replicas 发现这个请求已经接收到了，那么不要重新执行（尤其是不幂等的操作），而是简单重发（re-send）上次的计算结果。这需要日志功能。
   2. 如果 backup 发现之前没接收到过这个请求，那么就转发（relay）给 primary，并设置计时器，等待 primary 的广播。若等不到广播，那么就怀疑 primary 出问题了，可能是出现故障，也可能变成了恶意节点。

这里的 client 也可以是集群中的某个副本，比如 replica $i$ 想要更新自身状态保持与集群一致。

三段共识算法

在上述算法中的 step 2，需要让集群中的诚实节点对客户请求达成共识。共识算法分为三个阶段：pre-prepare，prepare，commit

阶段一：pre-prepare

1. primary 为请求消息$m$分配一个递增的序列号（sequence number）$n$，然后广播如下信息
   { { P R E − P R E P A R E , v , n , d } : p ,   m } \{\{PRE-PREPARE,v,n,d\}:p,\, m\} {{PRE−PREPARE,v,n,d}:p,m}
   其中$v$是视图号，$p=v\mathrm{mod}|R|$是 primary 的身份ID，$d=Hash(m)$是摘要。

   注意，pre-prepare 消息不包含客户指令，$m$作为第二个消息被广播。primary 将这两个消息记入自己的日志（log）里。

2. backup 接收到上述形式的 pre-prepare 消息和指令$m$后，依次检查：

   1. 是否满足$d=Hash(m)$，这关乎$m$的完整性
   2. 验证是否是$p$的合法签名，证明信息来源于 primary
   3. 自己是否位于视图$v$中
   4. 之前没接收过另一个 pre-prepare 消息$(v,n,d^{\prime }\ne d)$，否则可以怀疑 primary 是恶意节点
   5. 序列号$n$位于自己的高低水位（high/low water mark）$h,H$之间，这用于防止某节点落后其他节点太多。

   如果检查都通过，那么接受它们，并把它们写入日志。

阶段二：prepare

1. 如果 backup $i$ 接受了 pre-prepare 消息，那么它进入阶段二，对其他所有 replicas（包括 backup 和 primary）广播如下消息
   { P R E P A R E , v , n , d , i } : i \{PREPARE,v,n,d,i\}:i {PREPARE,v,n,d,i}:i
   并将这个 prepare 消息写入日志。

2. replica 接收到上述 prepare 消息后， 依次检查：

   1. 验证是否是$i$的合法签名，证明信息来源于 backup $i$
   2. 自己的当前视图是否等于$v$
   3. 序列号$n$位于自己的高低水位之间

   如果检查通过，那么接受它，并写入日志。

我们设置谓词（predicate）$prepared(m,v,n,i)$：它为真 $⟺$ 副本$i$的日志里记录了关于$m$的：$1$个来自 primary 的 pre-prepare 消息，$2f$个来自不同 backup（包含$i$自己）的 prepare 消息。

$prepared$谓词确定了请求事件$m_1,m_2,\cdots$在视图$v$下的全序（total order）：如果$prepared(m,v,n,i)=true$，那么对于任意的$m\ne m^{\prime }$，都有$prepared(m^{\prime },v,n,i)=false$，除非找到了Hash碰撞$Hash(m)=Hash(m^{\prime })$。

proof：因为有$1+2f$个 replicas 接收到了$(m,n)$的 pre-prepare 和 prepare 消息，且恶意节点至多有$f$个，那么就有$1+f$个诚实节点接收到了$(m,n)$，但一共就$3f+1$个节点，那么最多有$2f$个节点能接收到$(m^{\prime },n)$。除非有诚实节点对$(m,n),(m^{\prime },n)$都发送了 prepare 消息，这是不可能的。

阶段三：commit

1. 当 replica $i$ 发现$prepared(m,v,n,i)=true$，那么它就广播如下消息给所有的 replica
   { C O M M I T , v , n , d , i } : i \{COMMIT,v,n,d,i\}:i {COMMIT,v,n,d,i}:i
   并把它写入日志。

2. replica 接收到上述消息后，依次检查

   1. 验证是否是$i$的合法签名，证明信息来源于 replica $i$
   2. 自己的当前视图是否等于$v$
   3. 序列号$n$位于自己的高低水位之间

   如果检查通过，那么接受它，并写入日志。

我们设置两个谓词，

1. $committed(m,v,n)$：它为真 $⟺$ 存在$f+1$个诚实节点$S$，使得 $prepared(m,v,n,i)=true,\forall i\in S$
2. $committed-local(m,v,n,i)$：它为真 $⟺prepared(m,v,n,i)=true$ 并且 replica $i$ 的日志里记录了$2f+1$个来自不同 replica（包含自己）的 commit 消息

容易验证，
$$committed-local(m,v,n,i)=true\Rightarrow committed(m,v,n)=true$$
只要诚实的 replica $i$ 发现某些$(m,v,n)$对应的$committed-local(m,v,n,i)=true$，那么它就可以确定指令$m$已经被至少$f+1$个诚实节点所达成共识。它根据自身状态（集群状态的副本），按照序列号$n$从低到高，独立地执行$m$，将结果发送给对应的客户。

垃圾回收算法

在三阶段共识算法中，集群的每个节点都要写入大量的日志，除非它已经知道有$f+1$个诚实节点记录了这个消息，能够压倒$f$个恶意节点。为防止内存溢出，我们需要定期清理日志。然而，如果某条消息已经被多数诚实节点丢弃，但有一个节点没有记录它却需要使用它来修改自身状态，那么就不得不传输整个系统的状态了。因此，每个副本都需要定时证明自身状态是正确的。

实时生成证明（proofs）是昂贵的，所以我们利用序列号来设置一些检查点（checkpoint），一般选取$n\equiv 0\mathrm{mod}100$。拥有 proof 的检查点被叫做稳定检查点（stable checkpoint）

每个 replica 都维护若干个时刻的系统状态：$1$个最新稳定检查点，若干不稳定的检查点，还有当前状态（current state）。

1. 每当 replica $i$ 触碰到了新的检查点$n$（序列号为$n$的请求执行完毕），对应自身状态为$s$，那么广播如下消息
   { C H E C K P O I N T , n , d , i } : i \{CHECKPOINT,n,d,i\}:i {CHECKPOINT,n,d,i}:i
   其中$d=Hash(s)$。把这个 checkpoint 消息写入日志。

2. 每个 replica 收集其他节点发送的 checkpoint 消息，只需验证签名的正确性，并写入日志。直到收集到$2f+1$个消息，它们拥有相同的$(n,d)$，那么这些 checkpoint 消息就构成了系统状态$s$的proof，它成为了稳定检查点。

对于稳定检查点之前的（包括$n$）序列号对应的所有 pre-prepare、prepare、commit 消息，都是可以从日志中丢弃的。因为已经有$f+1$个诚实节点保持了相同的系统状态副本，这压倒了至多$f$个恶意节点。

我们将低水位$h$设为最新的稳定检查点，并且设置高水位$H$，使得$k=H-h$足够大，阻止恶意的 primary 发送大量 pre-prepare 消息来耗尽序列号空间，并且 replicas 也不必等待检查点变得稳定。可以设置为$k=200$

视图切换算法

1. 如果 backup $i$ 认为 primary 有问题，那么它广播（并非点对点发给$p=v+1$）视图切换请求，形式如下
   { V I E W − C H A N G E , v + 1 , n , C , P , i } : i \{VIEW-CHANGE,v+1,n,C,P,i\}:i {VIEW−CHANGE,v+1,n,C,P,i}:i

   • $n$：节点$i$知道的最新稳定检查点，对应系统状态$s$
   • $C$：对$s$的稳定性证明，那$2f+1$个 checkpoint 消息
   • $P$：集合$P_m$的集合，这里$P_m$包含节点$i$上严格大于$n$的序列号对应的请求$m$的有效的$1$个 pre-prepare 消息、$2f$个 prepare 消息，即$prepared(m,v,n,i)=true$

2. 如果 replica $p=v+1\mathrm{mod}|R|$ 收到了来自其他 replica（不含自己）的$2f$个有效的（检查签名、检查$C$、检查$P$） view-change 消息，那么它作为 primary 发起视图切换，广播如下信息
   { N E W − V I E W , v + 1 , V , O } : p \{NEW-VIEW,v+1,V,O\}:p {NEW−VIEW,v+1,V,O}:p

   • $V$：收到的$2f$个 view-change 消息，这证明有$f$个诚实节点认为视图$v$的 primary 有问题，视图变更是有必要的。

   • $O$：新视图下的 pre-prepare 消息集合，构建规则如下

     1. primary 查看$V$里的 view-change 消息，确定最近的稳定检查点$mi{n}_s$（拥有$C$，被$f+1$个诚实副本维护），以及 prepare 信息的最大序列号$ma{x}_s$（谓词 prepared 为真，在$f+1$个诚实节点上被准备）

     2. 对于每个序列号$n\in [mi{n}_s,ma{x}_s]$（闭区间）的请求，primary 创建它们在新视图$v+1$上的 pre-prepare 消息。如果$V$里存在一些 view-change 消息的$P$分量中包含$n$，那么设置
        { P R E − P R E P A R E , v + 1 , n , d } : p \{PRE-PREPARE,v+1,n,d\}:p {PRE−PREPARE,v+1,n,d}:p
        其中的$d$是在最高视图下 pre-prepare 消息里的摘要（似乎就是视图$v$下的？因为$V$中包含诚实节点的 view-change 消息，它本位于$v$视图，请求转换到$v+1$视图）

        如果没有这种分量（要么是$mi{n}_s=ma{x}_s$，要么序列号跳跃递增），那么设置
        { P R E − P R E P A R E , v + 1 , n , d n u l l } : p \{PRE-PREPARE,v+1,n,d_{null}\}:p {PRE−PREPARE,v+1,n,dnull​}:p
        这里的$d_{null}=Hash(null)$，空指令$null$

   primary 只将$O$写入自身日志，而$V$的内容已经在日志里了。如果$mi{n}_s$大于 primary 已知的稳定检查点，那么使用$mi{n}_s$作为自己的稳定检查点，记录它的proof，并清理过期数据。

3. replica 收到了上述 new-view 消息后，

   1. 验证签名的正确性
   2. 验证$V$是对于视图$v+1$的有效 view-change 消息集合
   3. 验证$O$是正确的 pre-prepare 消息集合，方法类似 step 2

   所有的校验都通过后，切换到$v+1$视图，将$V,O$写入日志，并为$O$里的每一个 pre-prepare 消息构造对应的视图$v+1$下的 prepare 消息并广播

4. replica 收到广播的 prepare 消息后，校验正确性，写入日志，并执行 commit 步骤，继续写日志。但是对于$n\in [mi{n}_s,ma{x}_s]$内的已经执行的请求，不要重新执行，而仅仅是重发存储下来的结果。

如果某节点丢失了一些请求信息，那么它直接从$O$中获取。如果它丢失了某个检查点的状态，那么它可以利用$V$中的 replica $i$ 的 view-change 消息找到稳定检查点$n$，然后向 replica $i$ 索要系统状态$s$。当然$s$过于巨大，可以通过状态分区（partition the state），记录各个区的状态最近被哪个序列号改变，那么就只需要更新一小部分状态即可。

其他

看到一篇 详解实用拜占庭协议PBFT 的文章，介绍了 视图协商、增删节点 的算法。论文 PBFT99 里没有给出描述，应该是其他人的相关工作。

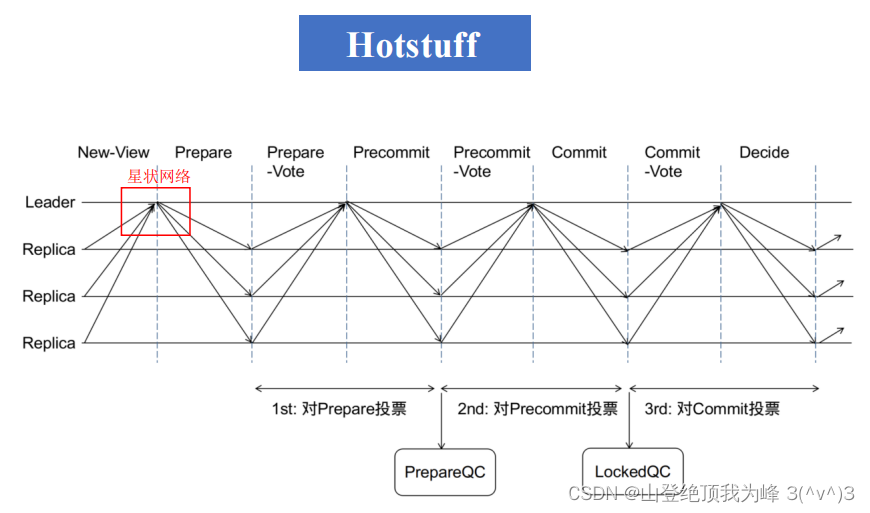
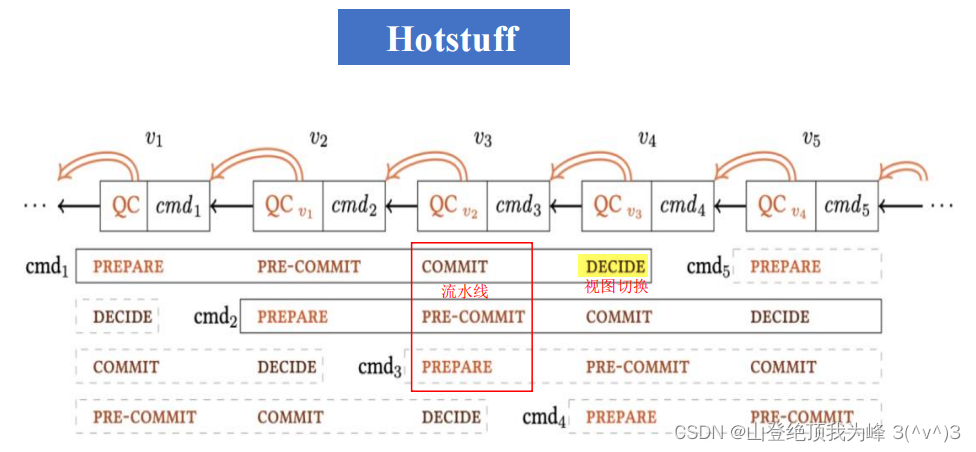
学习区块链课程时，了解到一种有意思的改进方案 Hotstuff。它使用星状网络大大降低了网络流量，并让三段共识算法流水线作业。论文没去找，等以后找时间看看。