1、拓扑排序 2、逆拓扑 3、i到j之间长度为k的路径 4、i到j之间包含顶点x的路径是否存在 5、如果边是带权的，求解 i 到 j 之间长度最长的路径

目录

1、拓扑排序

2、逆拓扑

3、i到j之间长度为k的路径

4、i到j之间包含顶点x的路径是否存在

5、如果边是带权的，求解 i 到 j 之间长度最长的路径

1、拓扑排序

/**
 * 内容：
 * 1、拓扑排序
 * 2、逆拓扑
 * 3、i到j之间长度为k的路径
 * 4、i到j之间包含顶点x的路径是否存在
 * 5、如果边是带权的，求解 i 到 j 之间长度最长的路径
 *
 * ①算法思想
 * 1、每一轮把一个入度为0的顶点加入到一个存储结构里面（栈或队列），然后从栈或队列中取出一个入度为0的元素，在图上做一个逻辑上的删除，
 * 删除后减少相关顶点的入度(GetIndegreeX)，再次将入度为0的顶点加入到存储结构里，直到逻辑删除完毕所有的顶点。
 * 2、有三种方法实现逆拓扑：
 * 法1：不断逻辑删除出度为0的顶点。（拓扑排序是不断删除入度为0的顶点）
 * 法2：使用DFS，可以想象一下，DFS 一直往深处遍历，直到遍历到这一轮的最后一个节点，说明这 
 * 个节点没有下一个了，说明没有出度，只有入度，那么理应是拓扑排序中的最后一个，那么也就是逆拓扑排序中的第一个。
 * 法3：先拓扑排序，最后一步将输出逆置。
 * 3、求i到j之间长度为 length 的路径（拿PathIsSimple（）改来的）
 * 4、i到j之间包含顶点 x 的路径（拿PathIsSimple（）改来的）
 * 5、如果边是带权的，求解 i 到 j 之间长度最长的路径（拿PathIsSimple（）改来的）
 *
 * ②算法设计
 *
 */
#include <stdio.h>
#include <iostream>
#include <cstdio>
#include <malloc.h>
#include <cstdlib>
#define MaxSize 20
#define INF 999999
 
 
struct ArcNode{
    int adjvex;
    struct ArcNode *next;
    int weight;
};
struct VNode{
    char value;
    struct ArcNode *first;
};
struct AdGraph{
    VNode vertices[MaxSize];
    int vexnum,arcnum;
};
 
//1、拓扑排序（可以判断有向联通图是否有环，如果不是连通图那么就对几个子部分分别进行判断）
//求顶点入度：
//复习：求某个顶点的入度：
//int GetInDegreeX(AdGraph G,int v){
//    int degree = 0;
//    ArcNode *p;
//    for (int i = 0; i < G.vexnum; ++i) {
//        p = G.vertices[i].first;
//        while(p){
//            if(p -> adjvex == v)
//                degree ++;
//            p = p -> next;
//        }
//    }
//    return degree;
//}
//求所有顶点入度：
void GetAllNodeInDegree(AdGraph G,int *indegree){
    for (int i = 0; i < G.vexnum; ++i) {
        ArcNode *p = G.vertices[i].first;
        while(p){
            indegree[p -> adjvex]++;//入度++
            p = p -> next;
        }
    }
}
//Topo函数
bool Topo(AdGraph G){
    int Stack[MaxSize],top = -1;//保存入度为0的顶点
    int indegree[MaxSize];
    int topoSequece[MaxSize],count = 0,v;//topoSequece[]用来保存拓扑序列，count用来标记存储到哪一块了
    for (int i = 0; i < G.vexnum; ++i) {
        indegree[i] = 0;
    }
    GetAllNodeInDegree(G,indegree);
    //把入度为0的顶点入栈
    for (int i = 0; i < G.vexnum; ++i) {
        if(indegree[i] == 0){
            Stack[++top] = i;
        }
    }
    while(top != -1){
        v = Stack[top--];
        topoSequece[count++] = v;//出栈后加入topo序列
        ArcNode *p = G.vertices[v].first;
        while(p){
            //下面两句也可以这样写：
            //if(!(--indegree[p -> adjvex]){...}
            indegree[p -> adjvex]--;
            if(indegree[p -> adjvex] == 0){
                Stack[++top] = p -> adjvex;
            }
            p = p -> next;
        }
    }
    //打印topoSequence
    for (int i = 0; i < count; ++i) {
        printf("%d ",topoSequece[i]);
    }
    if(count == G.vexnum)//说明拓扑序列里的元素数量和G的顶点数量相同，也就是所有元素都进入过Stack栈，说明所有元素逻辑上都入度为0过
        return true;
    else
        return false;
}

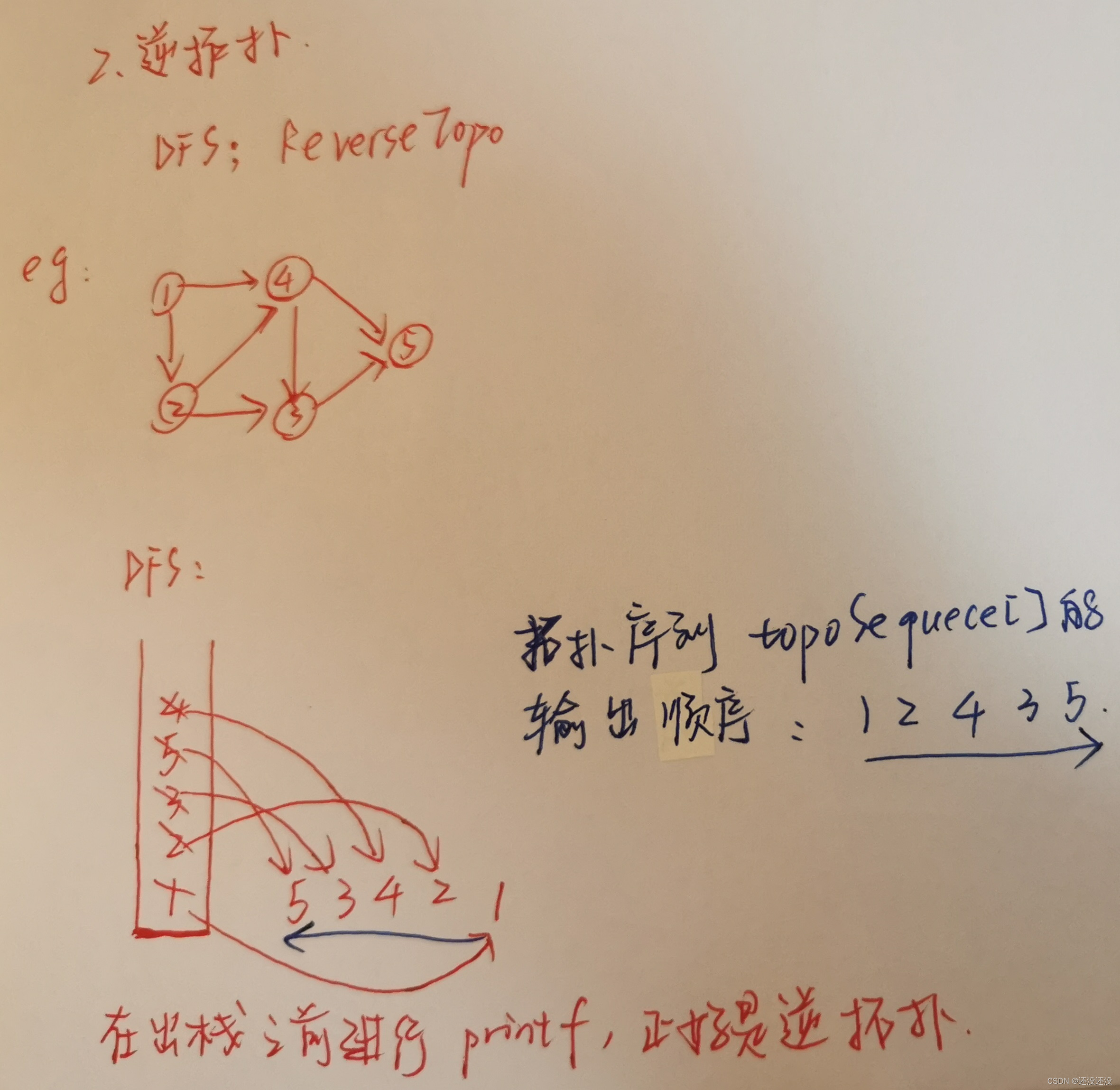
2、逆拓扑

//2、逆拓扑
//方法①：删除出度为0的节点
//求所有顶点出度：
void GetAllNodeOutDegree(AdGraph G,int *outdegree){
    for (int i = 0; i < G.vexnum; ++i) {
        ArcNode *p = G.vertices[i].first;
        while(p){
            outdegree[i]++;//出度++
            p = p -> next;
        }
    }
}
//逆Topo函数
bool ReTopo(AdGraph G){
    int Stack[MaxSize],top = -1;//保存入度为0的顶点
    int outdegree[MaxSize];
    int RetopoSequence[MaxSize],count = 0,v;//RetopoSequece[]用来保存拓扑序列，count用来标记存储到哪一块了
    for (int i = 0; i < G.vexnum; ++i) {
        outdegree[i] = 0;
    }
    GetAllNodeOutDegree(G,outdegree);
    //把出度为0的顶点入栈
    for (int i = 0; i < G.vexnum; ++i) {
        if(outdegree[i] == 0){
            Stack[++top] = i;
        }
    }
    //从网中将指向v顶点的顶点的度--
    while(top != -1){
        v = Stack[top--];
        RetopoSequence[count++] = v;//出栈后加入topo序列
        for (int i = 0; i < G.vexnum; ++i) {
            ArcNode *p = G.vertices[i].first;
            while(p){
                //下面两句也可以这样写：
                //if(!(--indegree[p -> adjvex]){...}
                if(p -> adjvex == v)
                    outdegree[i]--;
                if(outdegree[i] == 0){
                    Stack[++top] = i;
                }
                p = p -> next;
            }
        }
    }
    //将RetopoSequence数组里的元素输出
    for (int i = 0; i < count; ++i) {
        printf("%d ",RetopoSequence[i]);
    }
    if(count == G.vexnum)//说明拓扑序列里的元素数量和G的顶点数量相同，也就是所有元素都进入过Stack栈，说明所有元素逻辑上都入度为0过
        return true;
    else
        return false;
}
 
//方法②：使用DFS，DFS元素在出栈前进行输出就是逆拓扑（已知是无环的情况下才能使用DFS）
//回顾DFS
void DFS(AdGraph G,int v,int *visited){
    visited[v] = 1;
    printf("%c ",G.vertices[v].value);
    ArcNode *p = G.vertices[v].first;
    while(p){//边链表是断断续续访问完的
        if(!visited[p -> adjvex]){
            DFS(G,p -> adjvex,visited);
        }
        p = p -> next;
    }
}
//用DFS实现逆拓扑（已知是无环的情况下）
void ReverseTopo(AdGraph G,int v,int *visited){
    visited[v] = 1;
    ArcNode *p = G.vertices[v].first;
    while(p){//边链表是断断续续访问完的
        if(!visited[p -> adjvex]){
            ReverseTopo(G,p -> adjvex,visited);
        }
        p = p -> next;
    }
    printf("%d ",v);
}
 
//方法③：将拓扑排序序列逆置输出
//求所有顶点入度：
void GetAllNodeInDegree(AdGraph G,int *indegree){
    for (int i = 0; i < G.vexnum; ++i) {
        ArcNode *p = G.vertices[i].first;
        while(p){
            indegree[p -> adjvex]++;//入度++
            p = p -> next;
        }
    }
}
//逆Topo函数
bool ReTopo(AdGraph G){
    int Stack[MaxSize],top = -1;//保存入度为0的顶点
    int indegree[MaxSize];
    int RetopoSequence[MaxSize],count = 0,v;//RetopoSequece[]用来保存拓扑序列，count用来标记存储到哪一块了
    for (int i = 0; i < G.vexnum; ++i) {
        indegree[i] = 0;
    }
    GetAllNodeInDegree(G,indegree);
    //把入度为0的顶点入栈
    for (int i = 0; i < G.vexnum; ++i) {
        if(indegree[i] == 0){
            Stack[++top] = i;
        }
    }
    while(top != -1){
        v = Stack[top--];
        RetopoSequence[count++] = v;//出栈后加入topo序列
        ArcNode *p = G.vertices[v].first;
        while(p){
            //下面两句也可以这样写：
            //if(!(--indegree[p -> adjvex]){...}
            indegree[p -> adjvex]--;
            if(indegree[p -> adjvex] == 0){
                Stack[++top] = p -> adjvex;
            }
            p = p -> next;
        }
    }
    //将RetopoSequence数组里的元素逆置输出
    for (int i = count - 1; i >= 0; i--) {
        printf("%d ",RetopoSequence[i]);
    }
    if(count == G.vexnum)//说明拓扑序列里的元素数量和G的顶点数量相同，也就是所有元素都进入过Stack栈，说明所有元素逻辑上都入度为0过
        return true;
    else
        return false;
}

3、i到j之间长度为k的路径

//3、求i到j之间长度为length的路径
//d的初值是0
void PathIJ_length(AdGraph G,int i,int j,int *path,int d,int *visited,int length){//path是个数组，用于保存i到j的路径，d用来表示存入path数组的下标位置
    path[d] = i;
    if(i == j && d == length){
        for (int k = 0; k <= d; ++k) {//有个=是为了把j这个点的值也输出出来
            printf("%c ",G.vertices[path[k]].value);
        }
    }
    visited[i] = 1;
    ArcNode *p = G.vertices[i].first;
    while(p){//回退来之后，会直接走一下步没有被访问到的点，
        if(!visited[p -> adjvex]){//如果这个点没有被访问过，（保证了不会访问重复顶点）就调用自身
            PathIJ_length(G,p -> adjvex,j,path,d + 1,visited,length);
        }
         p = p -> next;
    }
    visited[i] = 0;
    //如果不置零，只能求出来一个唯一的长度为length的路径，但要求的是所有长度为length的路径。
    //因为某个顶点在这条长度为length的路径中被访问了之后，不一定说不是构成别的长度为length的路径所需要的顶点。
}

4、i到j之间包含顶点x的路径是否存在

//4、i到j之间包含顶点x的路径是否存在
//d的初值是0,刚开始is为0，代表不存在
void PathIJ_X(AdGraph G,int i,int j,int *path,int d,int *visited,int x,int &is){//path是个数组，用于保存i到j的路径，d用来表示存入path数组的下标位置
    path[d] = i;
    if(i == j){
        for (int k = 0; k <= d; ++k) {
            if(path[k] == x)
                is = 1;
        }
    }
    visited[i] = 1;
    ArcNode *p = G.vertices[i].first;
    while(p){//回退来之后，会直接走一下步没有被访问到的点，
        if(!visited[p -> adjvex]){//如果这个点没有被访问过，（保证了不会访问重复顶点）就调用自身
            PathIJ_X(G,p -> adjvex,j,path,d + 1,visited,x,is);
        }
        p = p -> next;
    }
    visited[i] = 0;//如果不置零，只能求出来一个唯一的路径，但要求的是所有简单路径。
    //因为某个顶点在这条路径中被访问了之后，不一定说不是别的路径所需要的顶点。
}

5、如果边是带权的，求解 i 到 j 之间长度最长的路径

//5、如果边是带权的，求解 i 到 j 之间长度最长的路径
struct MGraph{
    char vex[MaxSize];
    int weight[MaxSize][MaxSize];
    int vexnum,arcnum;
};
//d的初值是0,刚开始is为0，代表不存在
//有了路径之后，要保存路径的长度，新传入一个参数maxlength
void PathIJ_MaxLength(MGraph G,int i,int j,int *path,int d,int *visited,int &maxLength,int *maxPath,int count){
    //path是个数组，用于保存i到j的路径，d用来表示存入path数组的下标位置,
    //maxPath是个数组，用来拷贝maxLength最大的那个路径，也就是最长路径,count用来保存maxPath数组有多少个值,初值count=0
    path[d] = i;//path[]存的是路过的顶点的下标
    int sum = 0;//用来保存路径长度，刚开始是0
    if(i == j){
        //保存此条路径的长度
        for (int k = 0; k < d; ++k) {//这边不用再k=d了
            sum += G.weight[path[k]][path[k + 1]];//两顶点之间的长度
        }
        if(maxLength < sum){
            maxLength = sum;
            for (int k = 0; k <= d; ++k) {
                maxPath[count++] = path[k];
            }
        }
    }
    visited[i] = 1;
    for (int k = 0; k < G.vexnum; ++k) {
        if(G.weight[i][k] != 0 && G.weight[i][k] != INF && visited[k] == 0){
            //如果两点间有权值（即有边）并且不是INF并且这个点没有被访问过
            PathIJ_MaxLength(G,k,j,path,d,visited,maxLength,maxPath,count);
        }
    }
    visited[i] = 0;//如果不置零，只能求出来一个唯一的路径，但要求的是所有路径。
    //因为某个顶点在这条最长路径中被访问了之后，不一定说不是构成别的最长路径所需要的顶点。
}