Ceres Solver实例分析

ceres简介

Ceres solver 是谷歌开发的一款用于非线性优化的库，在谷歌的开源激光雷达slam项目cartographer中被大量使用。

本篇博客结合相关实例介绍一下 Ceres库 的基本使用方法：
使用Ceres求解非线性优化问题，一共分为三个部分：
1、 **第一部分：**构建cost fuction，即代价函数，也就是寻优的目标式。这个部分需要使用仿函数（functor）这一技巧来实现，做法是定义一个cost function的结构体，在结构体内重载（）运算符实现。
2、 **第二部分：**通过代价函数构建待求解的优化问题。
3、 **第三部分：**配置求解器参数并求解问题，这个步骤就是设置方程怎么求解、求解过程是否输出等，然后调用一下Solve方法。

实例分析

1）ceres求解最小值
案例一先看一个比较简单的案例，为Ceres官网教程给出的例程中：
使用ceres求取函数的最小值（很容易心算出x的解应该是10）
我使用的是Ubuntu20.04进行源码编译，为了让大家可自己动手编译实现，要在CMakeList.txt中添加：

find_package(Ceres REQUIRED)
include_directories(${CERES_INCLUDE_DIRS})
 
add_executable(ceretest src/ceretest.cpp)
target_link_libraries(ceretest ${CERES_LIBRARIES})
1
2
3
4
5

源码：

    #include 
    #include 
    using namespace std;
    using namespace ceres;
    //第一部分：构建代价函数
    struct CostFunctor {
        template <typename T>
        //operators是一种模板方法，其假定所的输入输出都变为T的格式
        //其中x为带估算的参数，residual是残差
        bool operator()(const T* const x, T* residual) const {
            residual[0] = T(10.0) - x[0]; //这里的T[10.0]，可以将10 转换位所需的T格式，如double，Jet等
            return true;
        }
    };
    //主函数
    int main(int argc, char** argv) {
        google::InitGoogleLogging(argv[0]);
        // 寻优参数x的初始值，为5
        double initial_x = 5.0;
        double x = initial_x;
        // 第二部分：构建寻优问题
        Problem problem;
        CostFunction* cost_function =
                new AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor); //使用自动求导，将之前的代价函数结构体传入，第一个1是输出维度，即残差的维度，第二个1是输入维度，即待寻优参数x的维度。
        problem.AddResidualBlock(cost_function, NULL, &x); //向问题中添加误差项，本问题比较简单，添加一个就行。
        //第三部分： 配置并运行求解器
        Solver::Options options;
        options.linear_solver_type = ceres::DENSE_QR; //配置增量方程的解法，使用得是稠密的QR分解方式
        options.minimizer_progress_to_stdout = true;//输出到cout
        Solver::Summary summary;//优化信息
        Solve(options, &problem, &summary);//求解!!!
        std::cout << summary.BriefReport() << "\n";//输出优化的简要信息
        //最终结果
        std::cout << "x : " << initial_x
                  << " -> " << x << "\n";
        return 0;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

结果为：
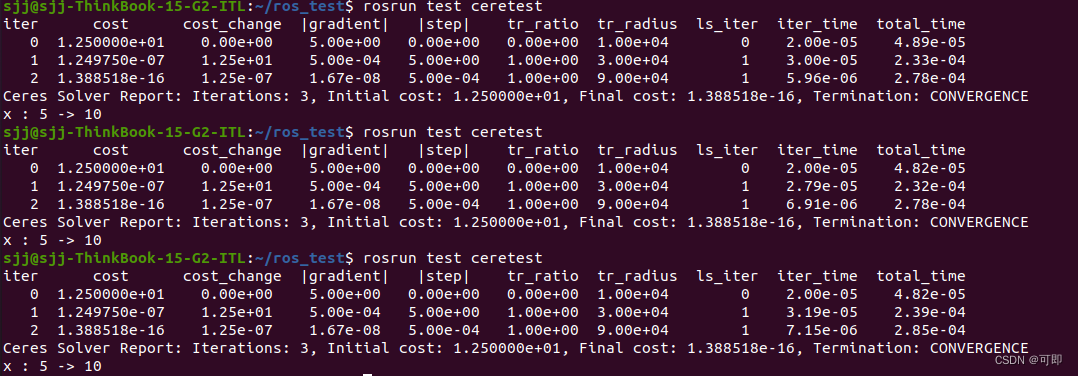Solve简要介绍：
使用ceres::Solve进行求解，其函数原型如下：

void Solve(const Solver::Options& options, Problem* problem, Solver::Summary* summary)
1

options：求解器的配置，求解的配置选项
problem：求解的问题，也即我们构建的最小二乘问题
summary：求解的优化信息，用于存储求解过程中的优化信息
1
2
3

对求解器的配置做如下说明：
Solver::Summary

Solver::Summary为求解器以及各个变量的信息，常用成员函数如下：

BriefReport()：输出单行的简单总结；
FullReport()：输出多行的完整总结。
1
2

2）ceres拟合曲线，（Curve Fitting）实现
有了上面的基础，现在用ceres来拟合非线性曲线，进阶一下：
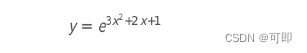整个代码的思路还是先构建代价函数结构体，然后在[0,1]之间均匀生成待拟合曲线的1000个数据点，加上方差为1的白噪声，数据点用两个vector储存（x_data和y_data），然后构建待求解优化问题，最后求解，拟合曲线参数。
（PS. 本段代码中使用OpenCV的随机数产生器，要跑代码的同学可能要先装一下OpenCV）

先给出代码：

#include
#include
#include
using namespace std;
using namespace cv;

//构建代价函数结构体，abc为待优化参数，residual为残差。
struct CURVE_FITTING_COST
{
  CURVE_FITTING_COST(double x,double y):_x(x),_y(y){}
  template <typename T>
  bool operator()(const T* const abc,T* residual)const
  {
    residual[0]=_y-ceres::exp(abc[0]*_x*_x+abc[1]*_x+abc[2]);
    return true;
  }
  const double _x,_y;
};

//主函数
int main()
{
  //参数初始化设置，abc初始化为0，白噪声方差为1（使用OpenCV的随机数产生器）。
  double a=3,b=2,c=1;
  double w=1;
  RNG rng;
  double abc[3]={0,0,0};

//生成待拟合曲线的数据散点，储存在Vector里，x_data，y_data。
  vector<double> x_data,y_data;
  for(int i=0;i<1000;i++)
  {
    double x=i/1000.0;
    x_data.push_back(x);
    y_data.push_back(exp(a*x*x+b*x+c)+rng.gaussian(w));
  }

//反复使用AddResidualBlock方法（逐个散点，反复1000次）
//将每个点的残差累计求和构建最小二乘优化式
//不使用核函数，待优化参数是abc
  ceres::Problem problem;
  for(int i=0;i<1000;i++)
  {
    //自动求导法，输出维度1，输入维度3,
    problem.AddResidualBlock(
      new ceres::AutoDiffCostFunction<CURVE_FITTING_COST,1,3>(
        new CURVE_FITTING_COST(x_data[i],y_data[i])
      ),
      nullptr,
      abc
    );
  }

//配置求解器并求解，输出结果
  ceres::Solver::Options options;
  options.linear_solver_type=ceres::DENSE_QR;
  options.minimizer_progress_to_stdout=true;
  ceres::Solver::Summary summary;
  ceres::Solve(options,&problem,&summary);
  cout<<"a= "<<abc[0]<<endl;
  cout<<"b= "<<abc[1]<<endl;
  cout<<"c= "<<abc[2]<<endl;
return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

这里由于有1000个点，所以需要对每个点计算一次残差，将所有残差累积在一起构成问题的总体优化目标，所以for循环1000次。
这里与前例不同的是需要输入散点的坐标x，y，由于_x，_y是结构体成员变量，所以可以通过构造函数直接对这两个值赋值。本代码里也是这么用的。

最终的运行结果是：
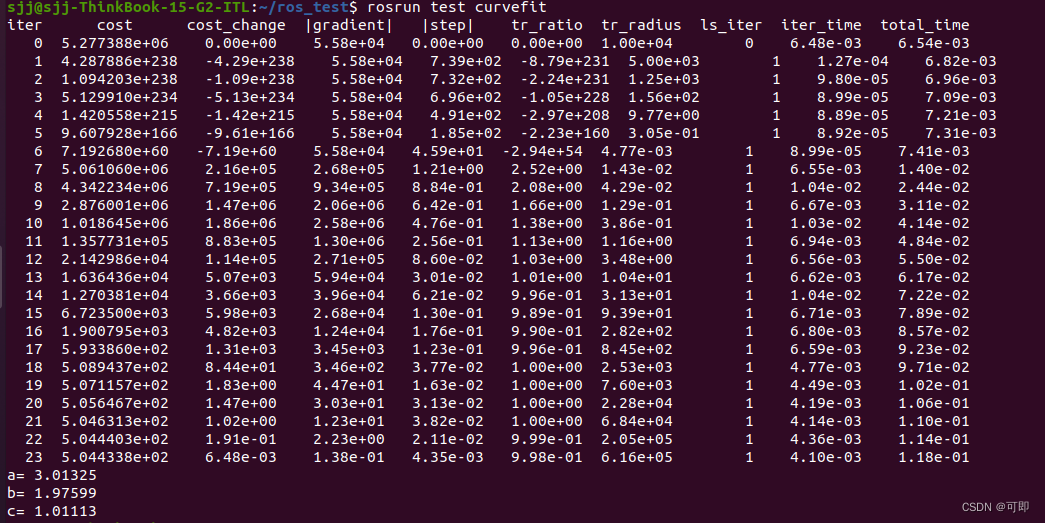可以看到，最终的拟合结果与真实值非常接近。

求解优化问题中（比如拟合曲线），数据中往往会有离群点、错误值什么的，最终得到的寻优结果很容易受到影响，此时就可以使用一些损失核函数来对离群点的影响加以消除。要使用核函数，只需要把上述代码中的NULL或nullptr换成损失核函数结构体的实例。
Ceres库中提供的核函数主要有：TrivialLoss 、HuberLoss、 SoftLOneLoss 、 CauchyLoss。
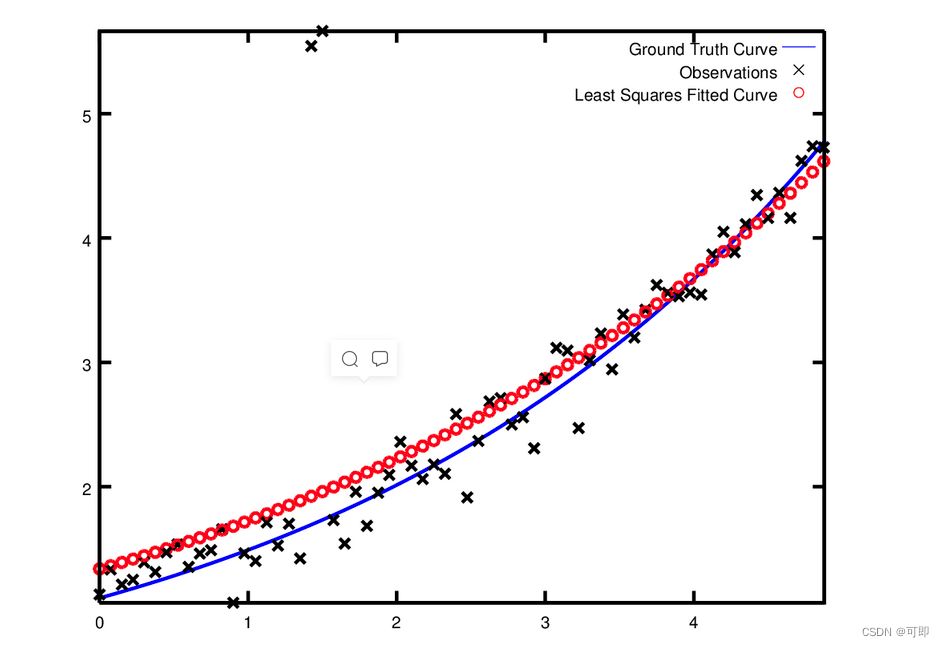
比如此时要使用CauchyLoss，只需要将nullptr换成new CauchyLoss(0.5)就行（0.5为参数）。

上述例子重新运行后结果：

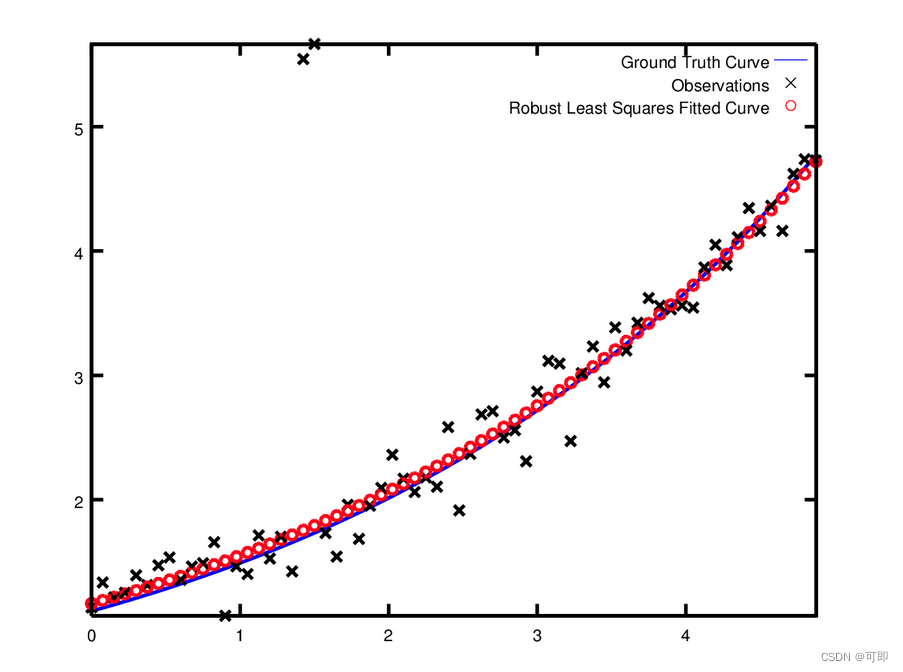
下面两图别为Ceres官网上的例程的结果，可以明显看出使用损失核函数之后的曲线收离群点的影响更小。