剑指offer--重建二叉树

Start

代码及分析

在已知前序遍历和中序遍历之后，如何建树呢？

我们知道，在二叉树的前序遍历当中，第一个数字总是根结点的值。而在中序遍历中，根节点位于中间位置，根结点的左边是左子树的结点，右边则是右子树的结点。

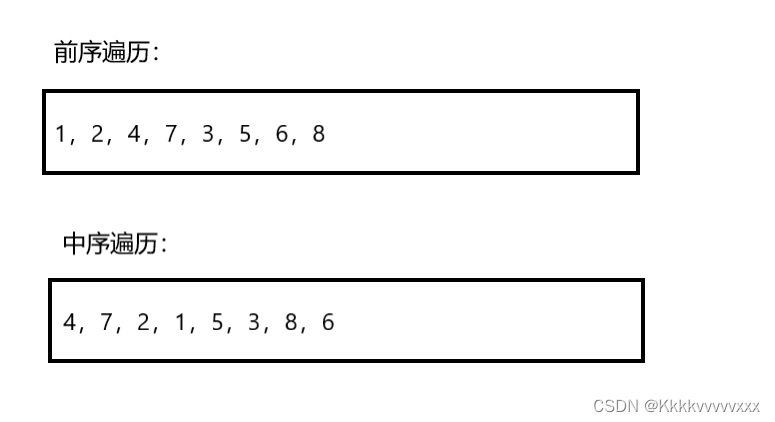
如上图，先序遍历的第一个数字就是根结点，在扫描中序遍历，就可以在中序遍历中确定根结点的位置；根结点的前面3个数字就是左子树结点的值，位于1后面的数字都是右子树结点的值！

现在已经找到根结点的左右子树的各结点，下来就需要进行建树；而建树的过程同样是寻找子树的根节点的一个过程，因此就需要用到递归的这一思路！

struct TreeNode
{
    int val;
    struct TreeNode* left;
    struct TreeNode* right;
};
struct TreeNode* reConstructBinaryTree(int* pre, int preLen, int* vin, int vinLen)
{
    struct TreeNode* Proot = 0;
    int flag = 0;

    if ((pre == NULL) || (preLen == 0))
        return NULL;
    Proot = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    memset(Proot, 0, sizeof(struct TreeNode));
    
    //前序遍历寻找根节点
    Proot->val = pre[0];
    
    //在中序遍历中寻找根节点
    while (pre[0] != vin[i])
    {
        ++flag;
    }
    //建树
    Proot->left = reConstructBinaryTree(pre + 1, flag, vin, flag);
    Proot->right = reConstructBinaryTree(pre + flag + 1, preLen - flag - 1, vin + flag + 1, vinLen - flag - 1);

    return Proot;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

下来先分析其递归过程：

在递归中，先处理左子树，将左子树建好后再递归到右子树建右子树，根据遍历结果我们先手动构思出树的形状。

1️⃣

当找到根结点后，先处理根结点，然后划分左右子树的结点。

2️⃣

先序遍历中找出2为左子树的根结点，处理后再次向下递归，此时会发现再将2处理完后，左子树的前序和中序遍历的数组存储的值是一样的，其实如果清楚二叉树的各种遍历的话以及观察遍历结果的话，不难想象出7是4的右子树。

3️⃣

4️⃣

根据遍历的结果可知，7应该是4的右子树。

在演示完左子树的所有结点的过程中，那么此时存在一个问题，我们该如何限定条件进行控制呢？

其实由上述图片，可以清晰的观察到，每一次先序遍历和中序遍历数组prev、vin都会少一个数值；而这个数值就是针对不同子树的根结点。所以在递归根节点的左右子树就要进行限制，左子树的限制：
Proot->left = reConstructBinaryTree(pre + 1, flag, vin, flag);prev每一次都是向后走，所以+1，而这个flag的含义就是每一次递归前所寻找到的根结点的位置。

reConstructBinaryTree(int* pre, int preLen, int* vin, int vinLen)，在函数中可以看到其实传递的flag就是数组的大小。

reConstructBinaryTree(pre + flag + 1, preLen - flag - 1, vin + flag + 1, vinLen - flag - 1);因为flag从0开始，所以控制数组时需要+1，而数组长度因此也需要-1即可，这一点根据例子就可以很好的体现出来！

右子树如图所示

Ending

关于上述的右子树我并没有画出来，原理与上述一致，而关于递归时的限定条件可以根据例子进行体会即可确定出来，用语言描述出来是有些拗口的。🙋‍♂️🙋‍♂️🙋‍♂️