Monte Carlo Algorithms

Monte Carlo Algorithms

1.计算Pi

我们采用随机数生成器近似$\pi$

---

假设平面上点$(x,y)$ 均匀在正方形内生成。

可以知道$(x,y)$在园内的概率$P=\frac{\pi }{4}$

---

由大数定律可知，当样本$n$足够大时，满足条件的点$m\approx \frac{\pi n}{4}$

因此$\pi \approx \frac{4m}{n}$

---

我们可以求出误差界限在$O(\frac{1}{\sqrt{n}})$，说明当$n$越大时，该方法求解的值会越近似$\pi$

---

总结

---

2.布封头针问题

该问题同样用来近似$\pi$。

---

随机在画有平行线的平面抛掷长为$l$的头针，与平行线相交的概率$P=\frac{2l}{\pi }$ ，该等式用微积分求解。

---

总结

---

头针问题的误差同样是$O(\frac{1}{\sqrt{n}})$，可以看到Lazzerini精确到小数点后七位，与$n=3408$时的误差不符，说明可能存在作假。

---

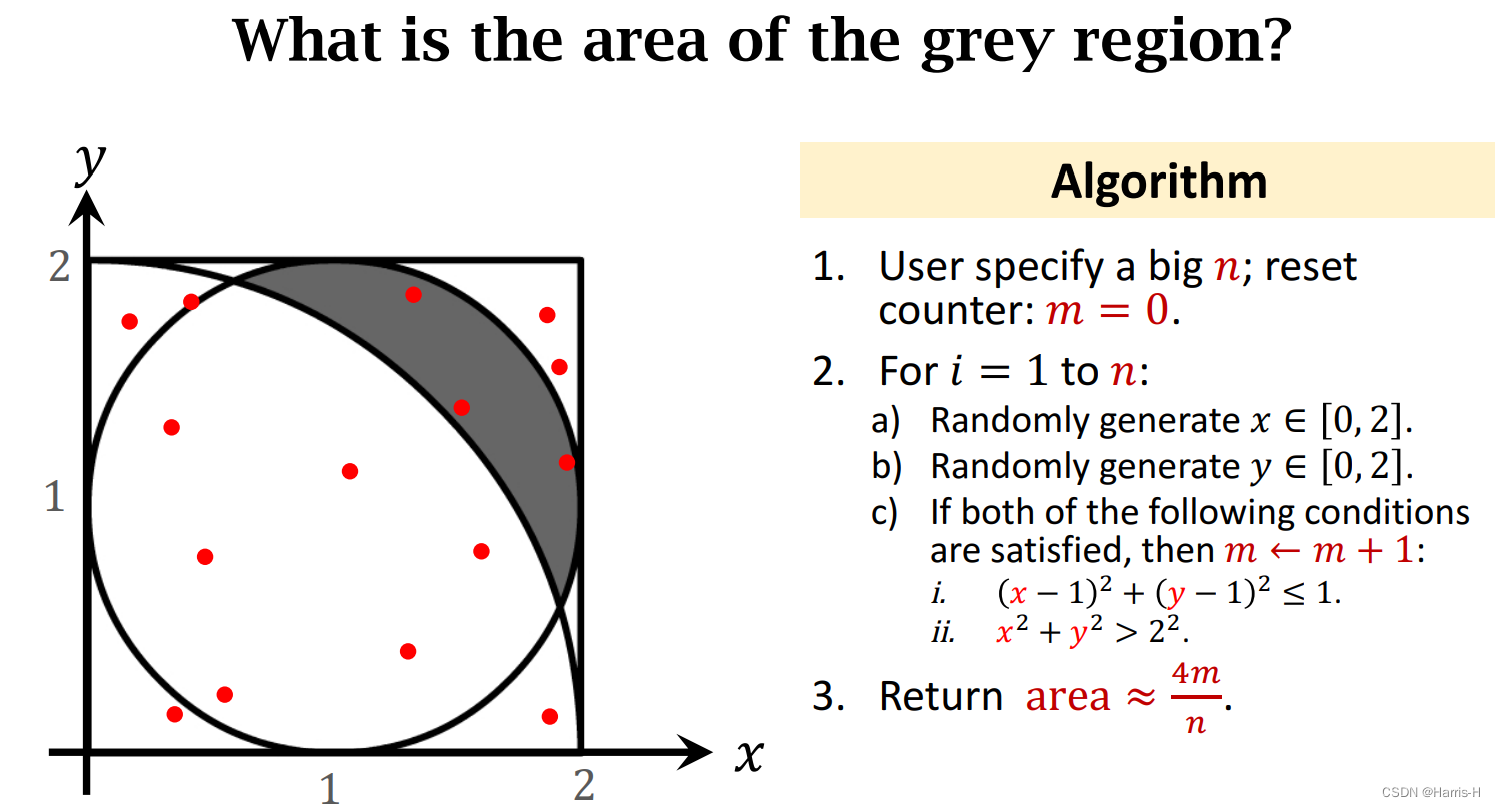
3.阴影面积计算

计算灰色区域面积。

---

可以分别判断点是否在扇形或者圆内。

---

通过1，2两个不等式便可以确定点$(x,y)$是否在阴影内。

---

我们可以知道点落在阴影内的概率为：$P=\frac{A_2}{4}$

---

总结

---

4.定积分

对于不可积的函数，我们可采用蒙特卡洛近似该区间的积分。

---

随机抽样$n$个点从区间$[a,b]$中。

$Q_n$等区间长度乘上$n$个点的均值。

根据大数定律，当$n\to \infty$， $Q_n\to I$

---

实例

---

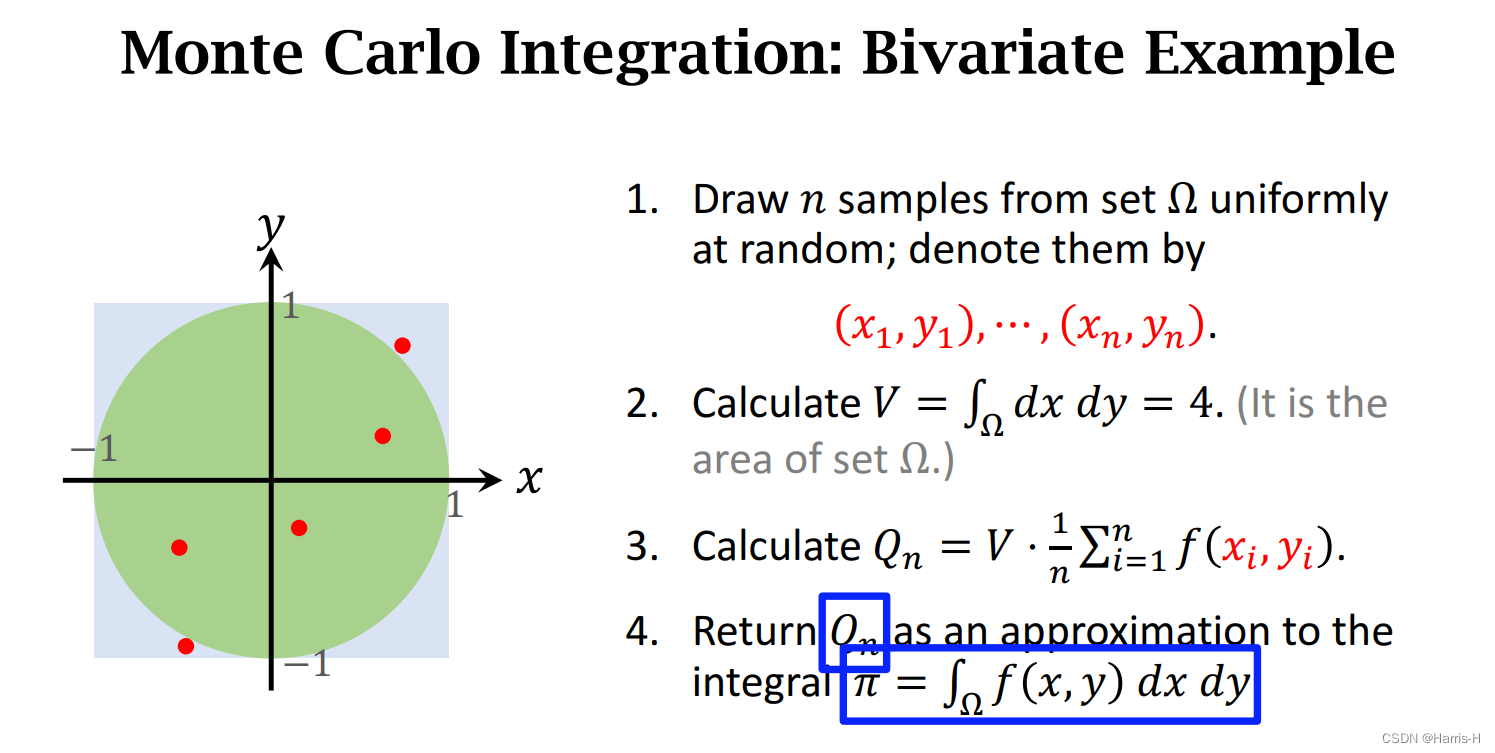
多维函数的积分

在空间$\Omega$下对多维x积分。

$Q_n$ 等于空间$\Omega$的体积乘上均值。

---

从另一个角度解释$\pi$的近似。

---

5.求期望

---

---

按照概率密度函数$p(x)$随机抽样$n$个样本，然后求均值$Q_n$可以近似期望$E_X$

---

6.蒙特卡洛算法的背景

由叫Nicholas Metropolis的第一次提出。

蒙特卡洛是一个赌城之都。

上面的拉斯维加斯等算法都是以赌场之都命名。

---