Leetcode 1584. 连接所有点的最小费用（手撸普利姆算法）

给你一个points 数组，表示 2D 平面上的一些点，其中 points[i] = [xi, yi] 。

连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 ：|xi - xj| + |yi - yj| ，其中 |val| 表示 val 的绝对值。

请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时，才认为所有点都已连接。

---

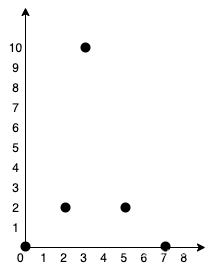
输入：points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
输出：20

解释：

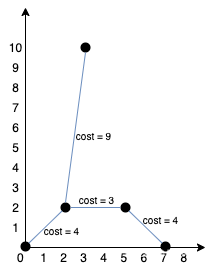
我们可以按照上图所示连接所有点得到最小总费用，总费用为 20 。
注意到任意两个点之间只有唯一一条路径互相到达。

---

【思路】：
明显的最小生成树问题。
可用普利姆算法解决。

简单概述一下普利姆算法的核心逻辑：

维护一个set，每次寻找距离set里所有节点最近的其他节点。找到后更新其他节点到set的距离，然后把该节点加入set。循环此过程，直到所有节点都被加入set集合。

可以把set想象成一个大岛屿，每次都是找其他节点到这个大岛屿的最短距离，找到后把该节点并入这个大岛屿。

---

【js代码】
这个算法理解思想之后代码还是比较好实现的

/**
 * @param {number[][]} points
 * @return {number}
 */

 //普利姆贪心算法
var minCostConnectPoints = function(points) {
    var set = [{x:points[0][0],y:points[0][1]}];          //普利姆集合
    var dis = new Array(points.length).fill(-1);        //各个点到集合的距离
    //生成集合到每个其他点的距离，初始化
    for(let i = 1;i < dis.length;i++){
        //let pointsIndex = i;
        dis[i] = Math.abs(set[0].x - points[i][0]) + Math.abs(set[0].y - points[i][1]);  
    }

    var res = 0;        //res为最后的最短距离
    //把每个节点都加入到集合set中
    while(set.length != points.length){
        //每次去找一个距离集合最近的节点。贪心算法。
        let min = Number.MAX_SAFE_INTEGER
        let minindex = -1;
        for(let i = 0;i < points.length;i++){
            let x = points[i][0];
            let y = points[i][1];
            //如果存在于集合内部就跳过
            if(dis[i] == -1)    continue;

            //let distence = dis[i];
            if(dis[i] < min)  {
                min = dis[i];
                minindex = i;
            }
        }
        //把最小的这个节点加入到集合中
        set.push({x:points[minindex][0], y:points[minindex][1]})
        //将集合到其他各个节点的最短距离更新
        dis[minindex] = -1;
        //更新dis数组
        for(let i = 0;i < points.length;i++){
            //到集合内部节点的距离无需更新
            if(dis[i] == -1)    continue;
            let distence = Math.abs(points[minindex][0] - points[i][0]) + Math.abs(points[minindex][1] - points[i][1]);
            dis[i] = Math.min(dis[i], distence)
        }
        res += min;
    }
    return res;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48