【论文阅读】MDK与MILDM

1、 MDK

1.1 摘要

提出了一种基于映射的鉴别核函数（Mapping-based Discriminative Kernel，MDK），用于更好地区分正负包。

首先，通过同时考虑包空间的局部性、包的辨别性能力以及包的代表性，构建了一个判别和代表包池（Discriminative and Representative bag Pool，DRP）。其中，局部性与代表性用于探索实例之间的关系，而判别性能力在挖掘标签信息的过程中使用。

第二，基于DRP将所有的包映射到基于DRP的判别性特征空间中。

第三，MDK将映射向量之间的相似性视为包间相似性，这保证了不同标签的包之间的差异以及相同标签的包之间的相似性。

DRP与常规方法的对比：

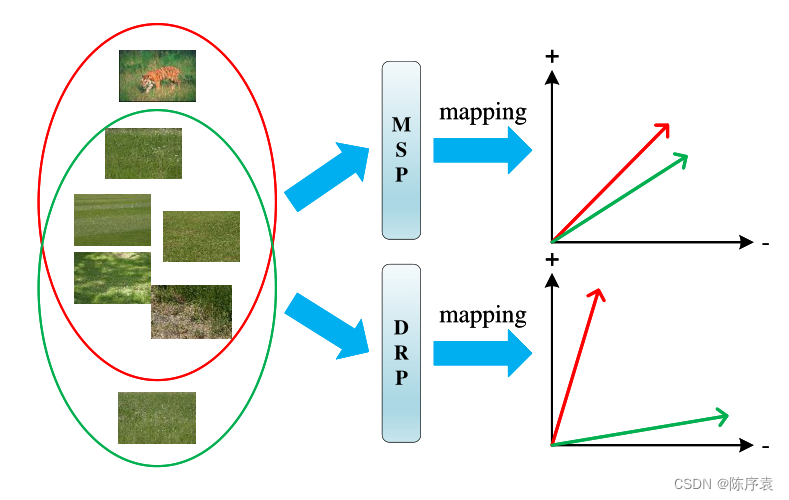
可以看出，DRP能够很好地区分映射空间中的正负包。

1.2 算法

· MDK

MDK的关键一步在于构建DRP。为了得到具有判别性能力的DRP，我们提出：最优DRP应确保具有相同标签的包在特征空间中彼此相似；带有不同标签的包应该体现它们之间的差异。DRP的评估公式表述为：
$$\mathcal{F}(\mathcal{P})=\frac{1}{2}\sum _{i,j}{D}_{\mathcal{P}}(B_i,B_j)Q_{i,j}\text{\hspace{1em}(1)}$$
其中，$\mathcal{P}$表示DRP，$D_{\mathcal{P}}(B_i,B_j)$表示在特征空间中两个包之间的距离，$Q_{i,j}$为嵌入了标签信息的矩阵$Q$的第$i$行$j$列元素值。

具体来说，$D_{\mathcal{P}}(B_i,B_j)$能够表示为：
$$D_{\mathcal{P}}(B_i,B_j)=||I{B}_i^{\mathcal{B}}-I{B}_j^{\mathcal{B}}|{|}_2^2\text{\hspace{1em}(2)}$$
其中，$I$是对角矩阵，对角线元素表示对应的包是否属于DRP。如果$B_i\in \mathcal{P},I_{i.j}=1$，否则为0。$B_i^{\mathcal{B}}$表示包$B_i$的映射向量，通过DRP中的包集$\mathcal{B}$映射：
$$B_i^{\mathcal{B}}=[s(B_i,B_1),...,s(B_i,B_N)]\text{\hspace{1em}(3)}$$
其中，$s()$为高斯相似性函数：
$$s(B_i,B_j)=e^{-\frac{d^2(B_i,B_j)}{{\sigma }^2}}\text{\hspace{1em}(4)}$$
其中，函数$d()$表示包间的平均豪斯多夫距离。

我们通过定义标签嵌入矩阵$Q$来同时考虑包的判别性与包空间的局部性。该矩阵$Q$定义为：
Q i , j = { − 1 a e d ( B i , B j ) , y i y j = 1 1 b e d ( B i , B j ) , y i y j = − 1 (5) Q_{i,j}=

\tag{5} Qi,j​=⎩⎪⎪⎨⎪⎪⎧​−aed(Bi​,Bj​)1​,bed(Bi​,Bj​)1​,​yi​yj​=1yi​yj​=−1​(5)
其中，$a$和$b$分别表示具有相同标签和不同标签的包对的数量，这体现了包的判别性。

包空间的局部性通过$e^{d(B_i,B_j)}$来体现。若包对标签相同，即$y_i{y}_j=1$，局部性能够使这两个相同标签的映射向量距离更近。若包对标签不同，即$y_i{y}_j=-1$，局部性能够使这两个不同标签的包映射向量距离更远。

通过将（1）式改写，能够得到包判别性能力得分：
KaTeX parse error: No such environment: split at position 7: \begin{̲s̲p̲l̲i̲t̲}̲ \mathcal{F}(\…

其中，$L$是由矩阵$Q$生成的拉普拉斯矩阵。${\psi }_g=[s(B_g,B_1),...,s(B_g,B_n)]$

因此，包$B_i$的可以判别性定义为：
$${\alpha }_i={\psi }_i^{T}L{\psi }_i\text{\hspace{1em}(7)}$$

· Bag representativeness metric

为了避免DRP中的包之间过于相似，需要考虑包的代表性。考虑两个部分：1）高局部密度$\rho$；2）与具有高局部密度的包保持较远距离$\delta$。即：DP聚类中的思想。

包$B_i$的代表性${\lambda }_i$定义为：
$${\lambda }_i={\rho }_i\cdot {\delta }_i\text{\hspace{1em}(8)}$$

通过计算每个包的判别性与代表性来得到每个包的得分$S_i$：
$$S_i={\alpha }_i\cdot {\lambda }_i\text{\hspace{1em}(9)}$$
得分用于判断某个包是否能够进入DRP。使用向量$S=[S_1,S_2,...,S_N]$来表示所有包的得分向量，并选出前$t$个有着最高得分的包来组成DRP。

用$k$来表示MDK，核矩阵$K$定义为：
$$K_{i,j}=k(B_i,B_j)=B_i^{{\mathcal{P}}^T}\cdot B_j^{\mathcal{P}}$$
其中，$B_i^{\mathcal{P}}$是包$B_i$通过DRP映射得到的向量，映射方式为：
$$B_i^{\mathcal{P}}=[s(B_i,P_1),...,s(B_i,P_t)]$$
其中，$P_i$是DRP中的第$i$个包。使用$V^{\mathcal{P}}=\left\{B_i^{\mathcal{P}},...,B_n^{\mathcal{P}}\right\}$来表示映射向量集。

· 算法流程

① 通过（5）式，同时考虑包的判别性与局部性，来得到包标签映射矩阵$Q$。判别性是通过统计包空间中的标签相同包对数量$a$与标签不同包队数量$b$。局部性是通过$e^{d(B_i,B_j)}$，能够让映射后的向量标签相同的离得更近，标签不同的离得更远；

② 将第①步中的矩阵$Q$转换为拉普拉斯矩阵$L(L=D-Q)$，再通过（7）式计算每个包的判别性得分${\alpha }_i$，（8）式计算每个包的代表性得分${\lambda }_i$。通过（9）式来综合以上两点，计算每个包的总得分$S_i$。

③ 通过计算所有包的得分并排序，找到前$t$高得分的包并组成DRP。

④ 将每个包与DRP中的$t$个包通过（4）式计算相似度，映射为$t$维向量。

⑤ 将包空间映射得到的向量通过SVM等分类器上进行学习。

2、MILDM

2.1、摘要

为了找出最佳实例，MILDM算法使得在映射空间中能够更好的区分包。可以使用选出的实例将每个包映射到新的特征空间中，成为映射向量。最后再使用svm等分类器进行分类预测。

2.2、算法

选择最佳实例组成DIP(discriminative instance pool)，用$\mathcal{P}$表示。在整个实例空间$\mathcal{X}$中找到子集$\mathcal{P}$，并将所有包$B_i$通过该子集映射成为向量$B_i^{\phi }=[s(B_i,x_1^{\phi }),...,s(B_i,x_k^{\phi })]$，其中$x_i\in \mathcal{P}$。算法的关键部分在于如何找到适用于包映射的DIP。

· DIP

通过实例选择矩阵${\mathcal{I}}_{\mathcal{P}}$（对角线矩阵，$diag({\mathcal{I}}_{\mathcal{P}})=d(\mathcal{P})$。若$x_i\in \mathcal{P}$，则$d(\mathcal{P}{)}_i=diag({\mathcal{I}}_{\mathcal{P}})=1$）找出实例集$\mathcal{P}\subseteq \mathcal{X}$组成DIP。

定义$\mathcal{J}(\mathcal{P})$作为实例选择函数，选出$m$个DIP分数最高的实例组成DIP实例集$\mathcal{P}$：
$$\begin{gathered} {\mathcal{P}}_{\ast }=\underset{\mathcal{P}\subseteq \mathcal{X}}{\mathrm{argmax}}\mathcal{J}(\mathcal{P}) \\ s.t.|\mathcal{P}|=m\text{\hspace{1em}(1)} \end{gathered}$$

在DIP中，需要保证相同标签的包映射后离得更近，不同标签的包映射后离得更远。DIP的评估函数定义为：
$$\mathcal{J}(\mathcal{P})=\frac{1}{2}\sum _{i.j}{K}_{\mathcal{P}}(B_i,B_j)Q_{i,j}\text{\hspace{1em}(2)}$$
其中，$K_{\mathcal{P}}(B_i,B_j)$表示通过DIP映射后在新的特征空间中包$B_i$与包$B_j$之间的距离，计算公式为：
$$K_{\mathcal{P}}(B_i,B_j)=||I_{\mathcal{P}}{B}_i^{{\phi }_x}-I_{\mathcal{P}}{B}_j^{{\phi }_x}|{|}^2\text{\hspace{1em}(3)}$$
其中，$B_i^{{\phi }_x}$与$B_i^{\phi }$生成的方式相同，使用所有实例作为映射实例池。

$Q$矩阵为标签映射矩阵，定义为：
Q i , j = { − 1 ∣ A ∣ , y i y j = 1 1 ∣ B ∣ , y i y j = − 1 (4) Q_{i,j}=

\tag{4} Qi,j​=⎩⎪⎪⎨⎪⎪⎧​−∣A∣1​,∣B∣1​,​yi​yj​=1yi​yj​=−1​(4)

重写（2）式，能够得到：
KaTeX parse error: No such environment: split at position 7: \begin{̲s̲p̲l̲i̲t̲}̲ \mathcal{J}(\…
其中，矩阵$L$是由矩阵$D$生成的拉普拉斯矩阵（$L=D-Q$，$D_{i,i}={\sum }_j{Q}_{ij}$是一个对角矩阵）。改写后的函数可以用$f(x_k^{\psi },L)$表示,，并以此函数来计算每个实例的得分：
$$\begin{gathered} \underset{\mathcal{P}\subseteq \mathcal{X}}{\max }\sum _{x_k^{\psi }\in \mathcal{P}}f(x_k^{\psi },L) \\ s.t.|\mathcal{P}|=m\text{\hspace{1em}(6)} \end{gathered}$$

· Bag Mapping via DIP

找出$m$个代表实例后，得到$\mathcal{P}$。通过将每个包与这$m$个代表实例求相似度，来将每个包映射成为特征空间中的$m$维特征向量：$B_i^{\psi }=[s(B_i,x_1^{\psi }),...,s(B_i,x_m^{\psi })]$。其中，相似性函数$s()$定义为：
$$s(B_i,x_k^{\psi })=\underset{x_{i,j}\in B_i}{\max }{e}^{-\frac{d^2(x_{i,j},x_k^{\psi })}{{\sigma }^2}}\text{\hspace{1em}(7)}$$
其中，$\sigma$为预设值。

· 算法流程

①将实例空间$\mathcal{X}$中的所有实例$x_i$通过（6）式计算它们的得分；

②选出前$m$个得分最高的实例，组成DIP；

③ 通过（7）式，将包空间中的所有包映射为向量，并将包空间映射得到的向量通过SVM等分类器上进行学习。

3、ELDB

3.1、摘要

由于标签是基于包给出的，多示例学习（MIL）比传统的监督学习更具一般性和挑战性。当前流行的特征映射方法是将每个包转化为新特征空间中的一个实例，但大多数映射方法难以保持包的区分度。
为了解决这一问题，本文提出了基于判别包的多示例集成学习算法（multi-instance ensemble learning with discriminative bags，ELDB），该算法通过两部分得到一个判别性包集（dBagSet）。
首先，考虑数据的空间分布与标签分布，通过判别性（discriminative）分析来优化包选择过程，得到基本包子集；其次，结合状态与动作转移策略，通过自强化获得区分度较好的包子集。

3.2、算法

与MILDM类似，ELDB通过计算每个包的分数来决定是否选择该包，对比（7）式：
$$p_k=b_k^{\ast }L(b_k^{\ast }{)}^T\text{\hspace{1em}(8)}$$
其中，$L$为判别性矩阵（$L=D-Q$，$D_{i,i}={\sum }_j{Q}_{ij}$是一个对角矩阵）。并选出前$\psi$个包组成${\mathcal{T}}_e$：
$$\underset{{\mathcal{T}}_e\subseteq {\mathcal{T}}_d\subset \mathcal{T}}{\max }\sum _{B_{{\xi }_k}\in \mathcal{T}}{p}_{{\xi }_k}\text{\hspace{1em}(9)}$$

得到判别包集合后，则利用判别包集合 T e = { B ζ k } k = 1 ψ ⊂ T \mathcal{T}_{e}=\left \{ \mathbf B_{\zeta k} \right \}_{k=1}^{\psi }\subset\mathcal{T} Te​={Bζk​}k=1ψ​⊂T,${\mathbf{B}}_i\in \mathcal{T}$对训练包集进行映射，映射方式为：
$$f_b({\mathbf{B}}_i,{\mathcal{T}}_e)\mapsto {\mathbf{b}}_i=[b_{i{\zeta }_1},...,b_{i{\zeta }_{\psi }}]\text{\hspace{1em}(10)}$$
因此，数据集将映射为：
f m ( T , T e ) ↦ V = { b i } i = 1 N (11) f_{m}(\mathcal{T},\mathcal{T}_{e})\mapsto V=\left \{ \mathbf{b_{i}} \right \}_{i=1}^{N}\tag{11} fm​(T,Te​)↦V={bi​}i=1N​(11)
通过计算两个包直接的平均豪斯夫距离（average Hausdorff distance）来度量关联性：
$$b_{ik}=||\overline{x_i}-\overline{x_k}||\text{\hspace{1em}(12)}$$
其中，$\overline{x_i}={\sum }_{j=1}^{n_i}{x}_{ij}/n_i$。

构建带权集成模型，将每一个dBagSet置入集成模型中。对每一个dBagSet进行映射，获取当前dBagSet的单实例分类模型以及权重：
$$M=f_c^{model}(V,Y)\text{\hspace{1em}(13)}$$
$$w=f_c^{weight}(V,Y,M)\text{\hspace{1em}(14)}$$

记录每个模型的预测结果，并处理每一个分类器和分类指标的预测结果，计算分类阈值。最终获得分类性能。