Python-计算两点经纬度之间的距离

计算两点经纬度之间的距离

经纬度是利用三维球面空间来描述地球上一个位置的坐标系统，每个经纬度坐标由经度 lng 和纬度 lat 两个分量组成。经纬度的有效范围为经度-180度到+180度，纬度大约-90度到+90度。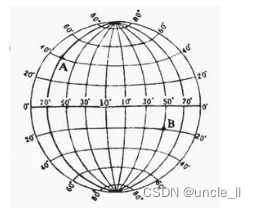

问题

给定两个点的经纬度，计算两个点的经纬度距离。

解决方法

Geopy是Python的包，用于计算两个地理位置的距离，它使开发人员更容易使用第三方地理编码器以及其他数据源来检索各个位置的坐标。

安装方式

pip install geopy
1

测地线距离|geodesic

测地线距离定义为空间中两点的局域最短路径， 但是是沿着曲面进行计算的，与任何两个给定位置之间的最短曲线不相同。下面说明如何用纬度和经度数据计算测地线距离。

# 导入geopy包
from geopy.distance import geodesic as GD

# pair数据格式，(latitude, longitude), 纬度和经度， 注意纬度和经度的取值范围
Abuja =(9.072264 , 7.491302)
Dakar =(14.716677 , -17.467686)

print("The distance between Abuja and Dakar is: ", GD(Abuja,Dakar).km)
# The distance between Nairobi and Cairo is: 2944.261368793268
1
2
3
4
5
6
7
8
9

大圆距离|great_circle

大圆距离指的是从球面的一点A出发到达球面上另一点B，所经过的最短路径的长度。在此示例中，假定地球是一个完美的球体。下面说明如何用纬度和经度数据计算大圆距离。

大圆距离将两个点分为两个弧，任何两个位置之间的较短弧等于大圆距离。

# 导入相应的包
from geopy.distance import great_circle as GRC

# pair对，纬度和经度
Abuja=(9.072264 , 7.491302)
Dakar=(14.716677 , -17.467686)


print("The distance between Abuja and Dakar is:", GRC(Abuja,Dakar).km) 
# The distance between Abuja and Dakar is: 2785.186971064666
1
2
3
4
5
6
7
8
9
10

Haversine formula|半正矢公式

半正矢公式是一种根据两点的经度和纬度来确定大圆上两点之间距离的计算方法，在导航有着重要地位。它是球面三角学中“半正矢定理”公式的特例，该定理涉及了球面三角形的边和角。

公式：

• 在弧度中，纬度的值是：

$$Latitude(LaA)=LaA/(180/\pi )或者Latitude(LaA)=LaA/57.29577$$

• 在弧度中，经度的值是：

$$Longitude(LoA)=LoA/(180/\pi )或者Longitude(LoA)=LoA/57.29577$$

我们使用以下公式计算英里的距离：

$$Distance(D)=3963.0\ast arccos[(sin(LaA)\ast sin(LaB))+cos(LaA)\ast cos(LaB)\ast cos(LoB-LoA)]$$

以下面的公式计算以公里为单位的距离：

$$Distance(D)=3963.0\ast arccos[(sin(LaA)\ast sin(LaB))+cos(LaA)\ast cos(LaB)\ast cos(LoB-LoA)]$$

from math import radians, cos, sin, asin, sqrt

def distance_d(LaA, LaB, LoA, LoB):
	LoA = radians(LoA)  
	LoB = radians(LoB)  
	LaA= radians(LaA)  
	LaB = radians(LaB) 

	D_Lo = LoB - LoA 
	D_La = LaB - LaA 
	P = sin(D_La / 2)**2 + cos(LaA) * cos(LaB) * sin(D_Lo / 2)**2  
   
	Q = 2 * asin(sqrt(P))   
	R_km = 6371  
	return(Q * R km).
 
LaA = 9.072264
LaB = 14.716677
LoA = 7.491302
LoB = -17.467686
print ("The distance between Abuja and Dakar is: ", distance_d(LaA, LaB, LoA, LoB), "K.M")  

# The distance between Abuja and Dakar is:  2785.183036572855 K.M
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

参考

• https://baike.baidu.com/item/%E7%BB%8F%E7%BA%AC%E5%BA%A6/1113442

• https://geopy.readthedocs.io/en/stable/#module-geopy.distance

• https://www.section.io/engineering-education/using-geopy-to-calculate-the-distance-between-two-points/