-
通信原理_1 信号与系统基础
一、介绍
现代通信原理一般是传输电信号。
香农模型:
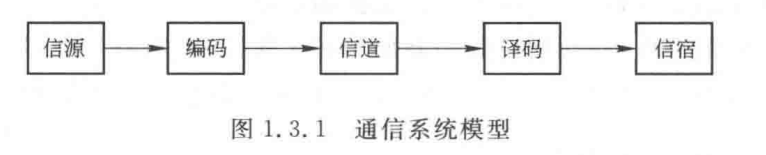
信源信息形式多种多样,编码时转换为处理更高效电信号。
信道一般有两种,第一种是在自由空间内传输的电磁波信号,第二种是沿导线传播的电磁波信号。
信道容量通常远大于用户传输的信息率。因此一般采用两种技术。
复用:多个信源的信号以正交的形式相互叠加,传输到目的地后再根据正交的原理拆分。
多址:多个信源的信号编码后直接传入信道,不叠加。

虚线代表通信网,中间的白点代表交换局,用于中转。
二、确定信号分析
能量 功率
能量: ∫ − ∞ + ∞ s 2 ( t ) d t \int_{-\infty}^{+\infty}s^2(t)dt ∫−∞+∞s2(t)dt
瞬时功率: s 2 ( t ) s^2(t) s2(t)
时移不改变能量和功率;信号*常数K,能量和功率都 *K^2.
一个信号的能量和功率不可能同时>0&&<无穷。能量有限的信号是能量信号,功率有限的信号是功率信号。
欧拉公式
e j θ = c o s θ + j s i n θ e^{j\theta}=cos\theta+jsin\theta ejθ=cosθ+jsinθ
复单频信号的频率: e j 2 π f t e^{j2\pi ft} ej2πft,f就是频率。
复信号的能量和功率是两个实信号的能量和功率之和。

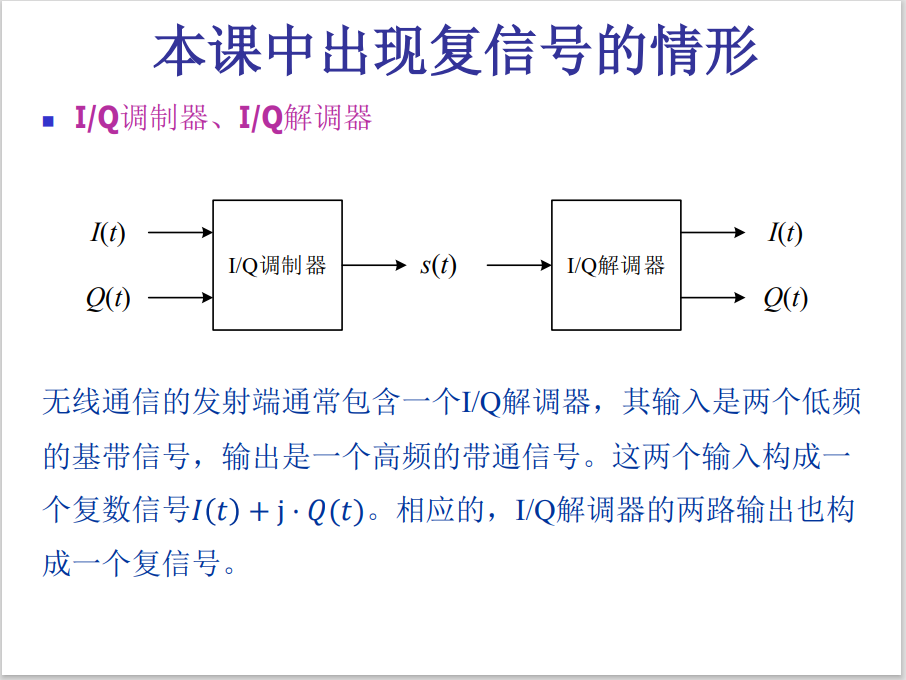

傅里叶级数和傅里叶变换

$ x(t)↔\int_{-\infty}{+\infty}X(f)e{j2\pi ft}df $
$ X(f)↔\int_{-\infty}{+\infty}x(t)e{-j2\pi ft}dt $
常用傅氏变换及性质
一个域中的面积是另一个域中原点处的值。
$ X(0)=\int_{-\infty}^{+\infty}x(t)dt $
$ x(0)=\int_{-\infty}^{+\infty}X(f)df $
时域越宽,频域越窄;时域越窄,频域越宽。
矩形傅氏变换
r e c t ( f T ) ↔ 1 T s i n c ( t T ) rect(fT)↔\frac{1}{T}sinc(\frac{t}{T}) rect(fT)↔T1sinc(Tt)
冲激与直流
δ ( t ) ↔ 1 \delta(t)↔1 δ(t)↔1
1 ↔ δ ( f ) 1↔\delta(f) 1↔δ(f)
时移与频移
x ( t − t 0 ) ↔ X ( f ) e − j 2 π f t 0 x(t-t_0)↔X(f)e^{-j2\pi ft_0} x(t−t0)↔X(f)e−j2πft0
x ( t ) e j 2 π f 0 t ↔ X ( f − f 0 ) x(t)e^{j2\pi f_0t}↔X(f-f_0) x(t)ej2πf0t↔X(f−f0)
镜像和共轭对称性
x(t)↔X(-f)
$ x*(t)↔X*(-f) $
因此如果x(t)是实信号,X(f)=X*(-f),满足共轭对称。


卷积与乘积
一个域的乘积,是另一个域的卷积。
冲激函数的乘积和卷积:
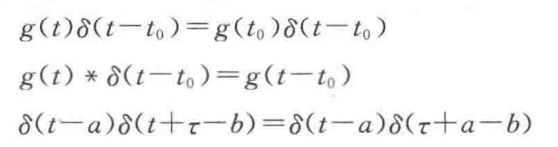
符号函数
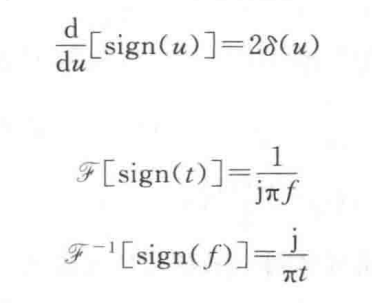
积分和微分

复单频信号和周期信号
$ e^{-j2\pi vt} $是复单频信号。

周期冲激序列

理想采样

-
相关阅读:
大模型时代,如何找准AI发展新方向?TVP读书会与你共探
Javaweb之HTML,CSS的详细解析
全栈开发笔记1:首个项目的收获
(02)Cartographer源码无死角解析-(18) SensorBridge→landmark与Imu的数据处理
【开源】基于Vue和SpringBoot的固始鹅块销售系统
机器学习-线性回归 二维问题
用 Hugging Face 推理端点部署 LLM
Matlab:非线性函数的运算
齐普夫定律在循环神经网络中的语言模型的应用
Python基础教程之十七:Python OrderedDict –有序字典
- 原文地址:https://blog.csdn.net/jtwqwq/article/details/126532534