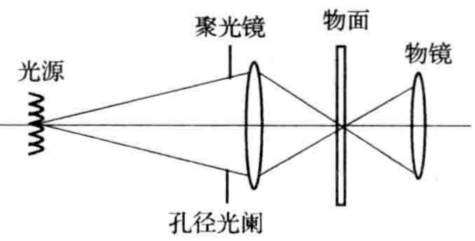
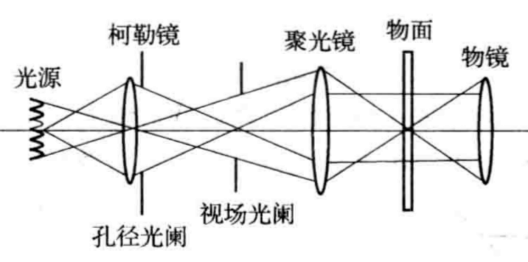
【工程光学】典型光学系统

ref

• 《工程光学复习指导与习题解答》第二版
• 工程光学-几何光学 思维导图

1.眼

• 人眼
  • 人眼本身相当于摄影光学系统, 角膜与视网膜之间的生物组织可视为像元, 物体经成像元成像在视网膜, 神经受刺激产生视觉. 人眼可通过肌肉调节改变等效光学系统的焦距, 使不同距离的物体自动清洗成像于视网膜.
  • 人眼瞳孔为孔径光阑, 可调节进入眼睛的光能.
• 调节
  • 眼睛成像系统对任意距离的物体自动调焦过程
  • $$\frac{1}{l_r}-\frac{1}{l_p}=R-P=A$$
    • $l_r$: 远点距离
    • $l_p$: 近点距离
    • 单位: 屈光度(D), 1D=100度
  • 明视距离: 为工作舒适,通常把物像置于眼前250mm处
• 正常眼: 眼睛远点在无限远/眼光学系统后焦点在视网膜
• 反常眼
  
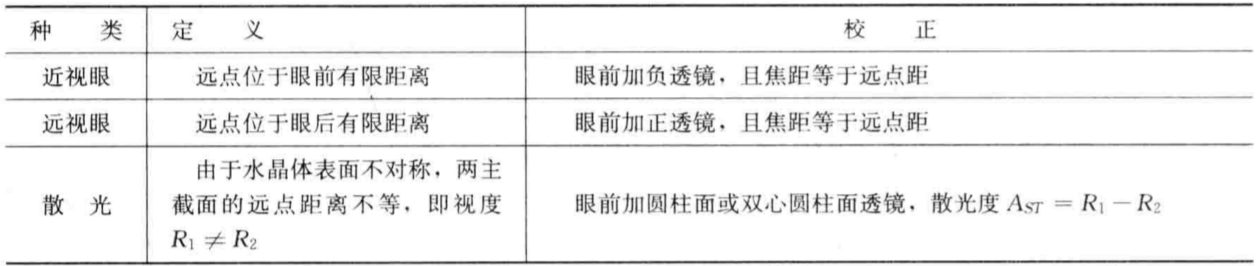
• 感光&感色: 视网膜是由锥状细胞与杆状细胞组成的辐射接收器
  • 杆状细胞: 对光刺激敏感, 不感色
  • 锥状细胞: 感光能力<杆, 感色, 决定分辨颜色的能力
  • 亮照明锥状细胞主导, 弱照明杆状细胞主导
  • 适应: 眼睛对周围空间亮度情况自动适应:明适应/暗适应
• 分辨率: 眼睛能分辨最靠近的两个相邻点的能力(视觉敏锐度)
  • 视角: 物体对人眼张角
  • 视觉鉴别率$\epsilon$: 良好照明条件下, 人眼能分辨物点间的最小视角, 松弛时$\epsilon =60^{\prime \prime }$
• 对准: 垂直于视轴方向上的置中或重合能力
  • 对准误差: 对准后偏离置中/重合的线距离/角距离
• 景深: 眼睛调节到某一对准平面时, 眼睛不必调节即可同时看清对准平面前后某距离物体的范围
  • $${\Delta }_1=\frac{P^2\epsilon }{D_p+P\epsilon }$$
  • $${\Delta }_2=\frac{P^2\epsilon }{D_p-P\epsilon }$$
  • $P$: 对准距离
  • $D_P$: 眼瞳直径
  • $\epsilon$: 人眼极限分辨角
• 立体视觉: 双目观察远近不同物体, 视差角${\theta }_A$不同, 肌肉紧张程度不同, 可分辨物体远近$L$
  • $${\theta }_A=\frac{b}{L}$$
  • 视差$\Delta \theta$: 不同距离的物体, 人眼对应不同视差角, 据其大小感觉两物体纵向深度
  • 体视锐度$\Delta {\theta }_{\min }$: 人眼能感觉到的$\Delta \theta$最小值, 常为$10^{\prime \prime }$
  • 立体视觉半径$L_{\max }=b/\Delta {\theta }_{\min }$: 人眼能分辨远近的最大距离
  • 立体视觉阈$\Delta L=\frac{\Delta \theta L^2}{b}$: 双眼能分辨两点间的最小距离

3.放大镜

• 能将放在焦点上/焦点附近的物体成放大虚像的目视透镜/透镜系统
• 视觉放大率$\Gamma$: 放大镜观察物体在视网膜的像高$y_i^{\prime }$ / 人眼直接观察物体时视网膜的像高$y_e^{\prime }$
  • $$\Gamma =\frac{y_i^{\prime }}{y_e^{\prime }}=\frac{l^{\prime }\tan {\omega }^{\prime }}{l^{\prime }\tan \omega }=\frac{\tan {\omega }^{\prime }}{\tan \omega }$$
    • ${\omega }^{\prime }$: 仪器观察物体时, 物体像对人眼张角
    • $\omega$: 人眼直接观察物体时, 物体对人眼张角
  • 放大率公式: 视觉放大率取决于观察条件
    • $$\Gamma =\frac{f^{\prime }-l^{\prime }}{P^{\prime }-l^{\prime }}\frac{D}{f^{\prime }}$$
    • 眼睛调焦到无限远$l^{\prime }=\infty$, 即物体位于物方焦面
      • $${\Gamma }_0=\frac{250}{f^{\prime }}$$
    • 像调焦到明视距离处, $P^{\prime }-l^{\prime }=D$
      • $$\Gamma =\frac{250}{f^{\prime }}+1-\frac{P^{\prime }}{f^{\prime }}$$
    • 人眼紧靠放大镜, $P^{\prime }\approx 0$
      • $$\Gamma =\frac{250}{f^{\prime }}+1$$
• 眼睛=孔径光阑,出瞳
• 放大镜=视场光阑,入窗,出窗,渐晕光阑

4.显微镜系统

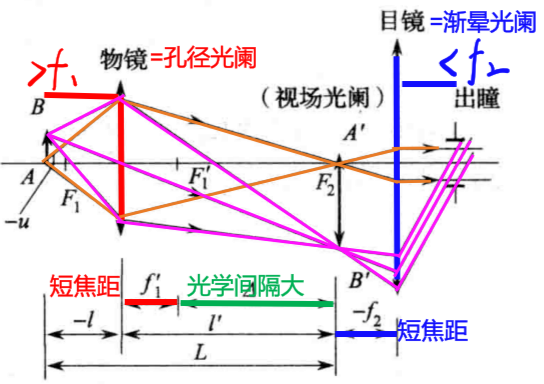
• 物镜,目镜焦距端, 光学间隔$\Delta$较大
• 成放大, 倒立实像
  • 物镜框=孔径光阑, 在像方焦平面形成物方远心光路
  • 一次实像面的分划板=视场光阑
  • 目镜=渐晕光阑
• 视觉放大率
  • $$\Gamma =\frac{\tan {\omega }^{\prime }}{\tan \omega }=-\frac{(250mm)\Delta }{f_o^{\prime }{f}_e^{\prime }}=\beta {\Gamma }_e$$
  • 物镜焦距$f_o^{\prime }$, 目镜焦距$f_e^{\prime }$, 显微系统焦距$f^{\prime }=-f_o^{\prime }{f}_e^{\prime }/\Delta$
• 线视场
  • $$2y=\frac{D}{\beta }$$
  • 视场光阑大小$D$
  • 为保持视场内成像良好, 视场光阑大小=目镜视场角$2{\omega }^{\prime }$
    • $$2y=\frac{500\tan {\omega }^{\prime }}{\Gamma }$$
• 分辨率: 能分辨近处两点的最小距离$\sigma$表示
  • 取决于数值孔径$NA=n\sin u$, 与目镜无关
  • 瑞利判断$\sigma =\frac{0.61\lambda }{NA}$
  • 道威判断$\sigma =\frac{0.5\lambda }{NA}$
  • 波长$\uparrow$ 分辨率$\downarrow$; 数值孔径$\uparrow$ 分辨率$\uparrow$
  • 有效放大率 $500NA\le \Gamma \le 1000NA$
• 景深
  • 数值孔径$\uparrow$ 放大倍率$\uparrow$ 景深$\downarrow$
  • 决定使用显微镜纵向调节的调焦误差
• 视度调节
  • 临界照明: 光能利用率高,照明不均
    • 
  • 柯勒照明: 照明均匀,光能利用率低
    • 

5.望远系统

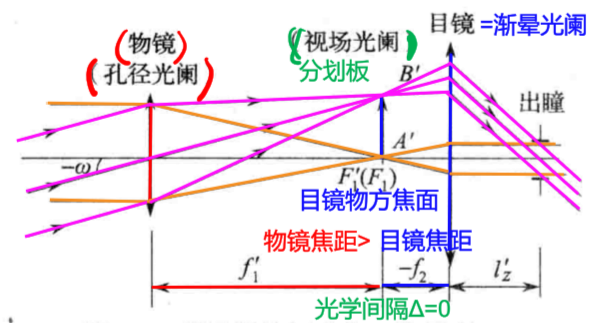
• 物镜焦距>目镜焦距, 光学间隔$\Delta =0$
  • 物镜框=孔径光阑
  • 一次实像面=视场光阑
  • 目镜=渐晕光阑, 影响轴外点成像的渐晕系数
• 视觉放大率
  • $$\Gamma =\frac{\tan {\omega }^{\prime }}{\tan \omega }=-\frac{f_1^{\prime }}{f_2^{\prime }}=-\frac{D}{D^{\prime }}$$
  • 获取大$\Gamma$, ++物镜焦距 / --目镜焦距
  • 开普勒望远镜: $f_1^{\prime }>0,f_2^{\prime }>0,\Gamma <0$
  • 伽利略望远镜: $f_1^{\prime }>0,f_2^{\prime }<0,\Gamma >0$
• 分辨率$\psi$
  • 瑞利判断$\psi =\frac{140^{\prime \prime }}{D}$, 道威判断$\psi =\frac{120^{\prime \prime }}{D}$
    • $D$望远系统入瞳的直径
  • 望远镜视觉放大率&分辨率$\psi \Gamma =60^{\prime \prime }$(人眼视觉分辨率), 一般视觉放大率取大2~3倍

6.摄影系统

• 组成
• 成像关系
• 光束限制
• 物镜主要参数
  • 焦距$f^{\prime }$像的大小
  • 相对孔径$D/f^{\prime }$
    • 像面照度,分辨率
  • 视场角$2\omega$
    • 成像范围
• 分辨率
  • $1/N=1/N_L+1/N_r$, $N_L=1/\sigma =D/1.22\lambda f^{\prime }$
• 光圈
  • 光圈数 $F{f}^{\prime }/D$
  • 光圈$\uparrow$F$\downarrow$, 光圈$\uparrow$ 2a $\uparrow$, 光圈$\uparrow$分辨率$\uparrow$, 光圈$\uparrow$像面照度$\uparrow$, 光圈$\uparrow$景深$\downarrow$
• 景深
  • 2a$\uparrow$ $\Delta$ $\downarrow$, P$\uparrow$ $\Delta$ $\uparrow$, $f^{\prime }$ $\uparrow$ $\Delta$ $\downarrow$
• 摄影物镜种类
  • 普通, 大孔径, 广角, 远摄, 变焦距

投影系统

• 系统基本要求
  • 像差,照明
• 主要光学参数
  • $$\beta =y^{\prime }/y$$
  • $$f^{\prime }\approx \frac{l^{\prime }}{1-\beta }$$
  • $$\tan {\omega }^{\prime }=\frac{y^{\prime }}{l^{\prime }}=\frac{\beta y}{f^{\prime }(1-\beta )}$$
  • $$\frac{D}{f^{\prime }}=2(1-\beta )\sqrt{\frac{E_0}{\tau \pi L}}$$
• 照明系统衔接条件
  • 照明系统拉赫不变量>投影系统拉赫不变量
  • 保证光瞳衔接与成像关系