🧸🧸🧸各位大佬大家好，我是猪皮兄弟🧸🧸🧸

今天带来的内容是堆

这里是下面要讲的知识内容🥳🥳🥳

---

一、⚽堆的性质及概念

堆是一种查找算法

堆的性质：
1.堆中某个节点的值总是不大于或者不小于其父节点的值
2.堆总是一颗完全二叉树
大根堆与小根堆

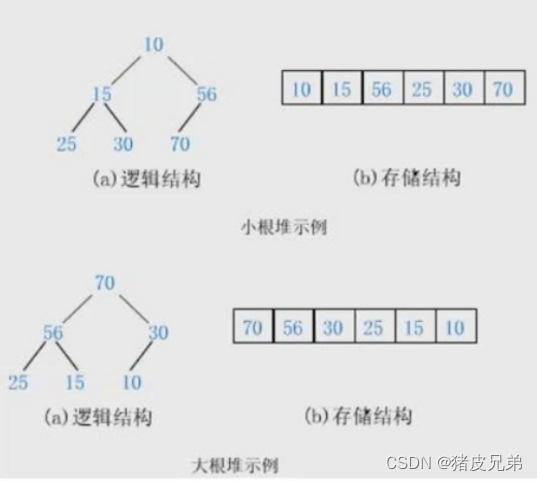
升序打印 ---- 小堆，因为要取最小值
降序打印 ---- 大堆，因为要取最大值

二、⚽堆的作用

1.堆排序，时间复杂度O(NlogN)
2.topk问题，多个数据选出前k个

三、⚽小堆的插入与删除操作(也有递归)

因为堆是一颗完全二叉树，所以，我们采用顺序存储，而不采用链式存储

//小堆的插入
void Swap(HPDataType*x,HPDataType*y)
{
	assert(x&&y);
	int tmp=*x;
	*x=*y;
	*y=tmp;
}
void AdjustUp(HPDataType*a,int child)
{
	assert(a);
	int parent=(child-1)/2
	while(child>0)
	{
		if(a[child]<a[parent])
		{
			swap(&a[child],a[parent]);
			child=parent;
			parent=(child-1)/2;
		}
		else
		{
			break;
		}
	}
}

void HeapPush(HP* php,HPDataType x)
{
	assert(php);
	HPCheckCapacity(pho);
	//因为顺序表涉及到扩容的问题
	php->a[php->size]=x;
	php->size++;
	//在顺序表的最后插入，然后再进行向上调整
	AdjustUp(php->a,php->size-1);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

小堆的删除思想就是将最小的a[0]和a[size-1]上的换一下，然后pop掉顺序表的最后一个，再将换过去的数据向下调整

//小堆的删除
void AdjustDown(HPDataType*a,int size,int parent)
{
	assert(php->a);
	int child=parent*2+1;
	while(child<size)
	{
		if(child+1<size&&a[child]>a[child+1])
		{
			child++;
		}
		if(a[child]<a[parent])
		{
			Swap(&a[child],&a[parent]);
			parent=child;
			child=2*parent+1;
		}
		else
		{
			break;
		}
	}
	
}
void HeapPop(HP*php)
{
	assert(php);
	assert(php->size>0);
	Swap(&(php->a[0]),&(php->a[php->size-1]));
	php->size--;
	AdjustDown(php->a,php->size,0);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

如果a[parent]>a[child]一直往下递归，一旦不成立就停止

//向下调整的递归
void AdjustDown(HPDataType*a,int size,int parent)
{
	int child=2*parent+1;
	if(child+1<size&&a[child+1]<a[child])
	{
		Swap(&a[child],&a[parent]);
		parent=child;
		if(parent*2+1<size)
			AdjustDown(a,size,parent);
		else
			return;
	}
	else
		return ;
}


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

小堆和大堆的向上向下调整if的条件变一下就行了

---

四、⚽堆排序

1.🌈两种建堆方式

向上调整建堆和向下调整建堆

void HeapSort(int*a,int n)
{

	//建堆方式1：向上建堆
	for(int i=1;i<n;++i)
	{
		AdjustUp(a,i);
	}
	
	//因为向下调整建堆需要左右子树都是堆才能调整，所以，从下往上，并且，从有意义的开始，也就是最后一个数据的parent
	for(int i=(n-1-1)/2;i>=0;i--)
	{
		AdjustDown(a,n,i);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

2.🌈堆排序的时间复杂度分析

向下调整建堆O(N)
采用每一层的结点数*最坏轻快下的调整次数，然后错位相减
分析如下

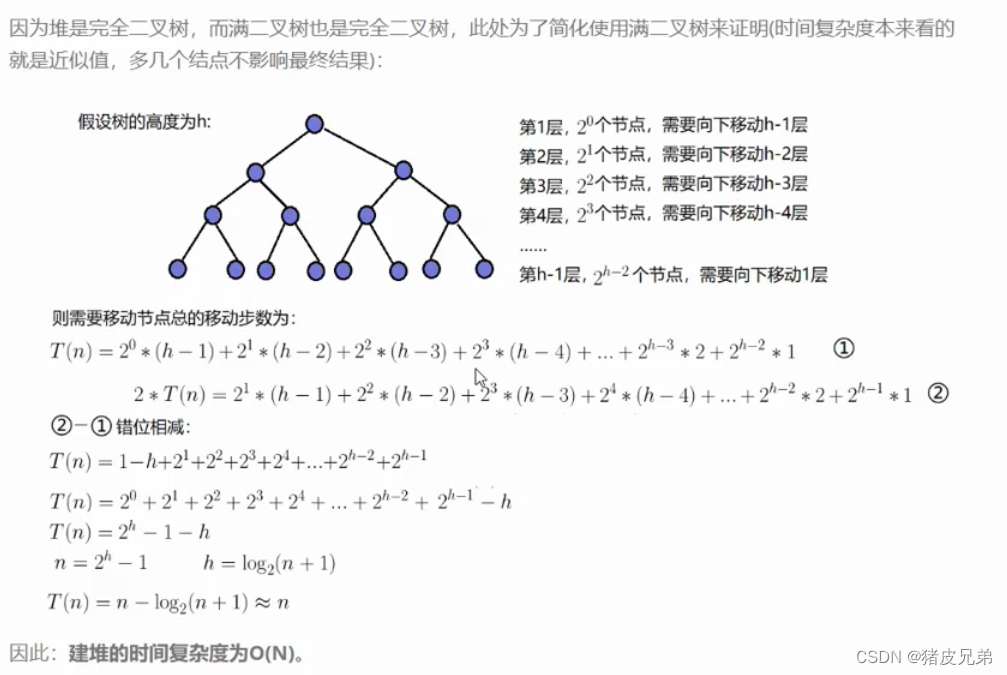
向上调整建堆O(NlogN)
几乎每一个结点都需要向上调整，然后最坏情况下调整logN次，所以N*logN

3.🌈大小堆的选择问题

用堆来进行取（HeapTop），再HeapPop操作的话
1.升序用小堆，每次取最小值
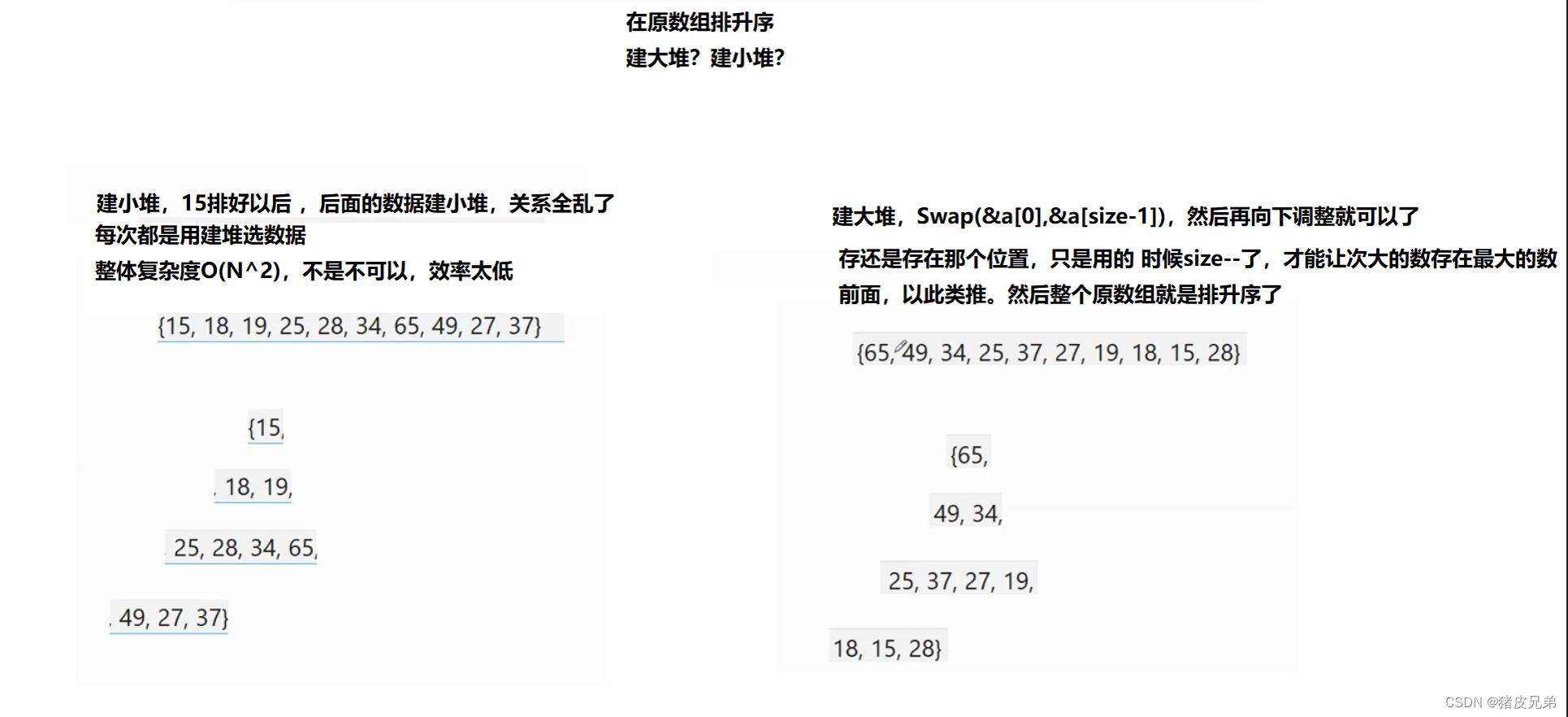
2.降序用大堆，每次取最大值

而如果想再原数组上进行操作的话
1.排升序，建大堆，取出最大的和最后的数据交换，Swap(&a[0],&a[size-1])
2.排降序，建小堆，取出最小的和最后的数据交换，Swap(&a[0],&a[size-1])

五、⚽TOP-K问题

建立k个数据的堆，后面的N-k和最小的比较，所以要是小堆，不然怎么找最小的，其次最后要堆这些留下来的数据降序，所以建小堆（前面说过）

TOP-K问题：即求数据结构中前k个最大的元素或者最小的元素，一般情况下数据量都比较大。
比如：专业前10名，世界500强，富豪榜、游戏中前100的活跃玩家等
对于TOP-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太现实了（可能数据都不能一下子全部加入到内存中，最佳的方式就是用堆来解决）
TOP-K就是从N个数中找出最大或者最小的前k个

找最大的前k个
1、排序O(NlogN) 比如堆排序，快排
2、建N个数的大堆 HeapTop/HeapPop k次 O(N+klogN)
3、假设N非常大，比如N是100亿，k比较小，k是100，如何求解？（本质上是空间效率更高）

void PrintTopK(int *a,int n,int k)
{
	int *kMinHeap=(int*)malloc(sizeof(int)*k);
	assert(kMinHeap);
	for(int i=0;i<k;i++)
	{
		kMinHeap[i]=a[i];
	}
	for(int i=(k-1-1)/2;i>=0;--i)
	{
		AdjustDown(kMinHeap,k,i);
	}
	for(int j=k;j<n;++j)
	{
		if(a[j]>kMinHeap[0])
		{
			kMinHeap[0]=a[j];
			AdjustDown(kMinHeap,k,0);
		}
	}
	for(int i=0;i<k;i++)
	{
		Printf("%d ",kMinHeap[i]);
	}
	printf("\n");
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

---

六、⚽总结

堆排序是一种很快的算法，可以匹敌快排了，需要好好的掌握一下，下一篇内容是二叉树oj