-
知识表示学习(四):TransD
一.摘要
知识图谱是许多 AI 应用程序的有用资源,但它们远非完整。 以前的工作如 TransE、TransH 和 TransR/CTransR 将关系视为从头实体到尾实体的转换,并且 CTransR 实现了最先进的性能。在本文中,我们提出了一种更细粒度的模型,称为 TransD,它是对 TransR/CTransR 的改进。 在 TransD 中,我们使用两个向量来表示一个命名符号对象(实体和关系)。第一个表示实体(关系)的含义,另一个用于动态构造映射矩阵。与TransR/CTransR相比,TransD不仅考虑了关系的多样性,还考虑了实体。 TransD 参数较少,没有矩阵向量乘法运算,可以应用于大规模图。
二.背景介绍
WordNet、Freebase 和 Yago 等知识图谱在关系提取 (RE)、问答 (Q&A) 等许多 AI 应用中发挥着举足轻重的作用) 等。它们通常包含大量结构化数据,以三元组(头实体、关系、尾实体)的形式(表示为 (h, r, t)),其中关系对两个实体之间的关系进行建模。由于大多数知识图谱要么是协作构建的,要么是(部分)自动构建的,因此它们经常遭受不完整的困扰。知识图谱补全是根据知识图谱中已有的三元组来预测实体之间的关系。在过去的十年中,基于符号和逻辑的知识图谱补全已经做了很多工作,但是对于大规模的知识图谱来说,它们既不易于处理,也不够收敛。最近,这项任务的一种强大方法是将知识图谱的每个元素(实体和关系)编码到低维嵌入向量空间中。这些方法通过代数运算对知识图进行推理。
在这些方法中,TransE (Bordes et al. 2013) 简单有效,并且还实现了最先进的预测性能。它为知识图中的每个实体和关系学习低维嵌入。这些向量嵌入由相同的粗体字母表示。基本思想是每个关系都被视为嵌入空间中的平移。对于一个黄金三元组 (h, r, t),通过添加嵌入 r,嵌入 h 接近于嵌入 t,即 h + r ≈ t。 TransE 适用于 1 对 1 关系,但在处理 1 对 N、N 对 1 和 N 对 N 关系时存在缺陷。 TransH (Wang et al. 2014) 被提出来解决这些问题。 TransH 将关系视为关系特定超平面上的平移操作,其特征在于范数向量 wr 和平移向量 dr。嵌入 h 和 t 首先投影到关系 r 的超平面上,得到向量 h⊥ = h − w>r hwr 和 t⊥ = t − w> r twr,然后是 h⊥ + dr ≈ t⊥。在 TransE 和 TransH 中,实体和关系的嵌入都在同一个空间中。然而,实体和关系是不同类型的对象,在同一个空间中对它们进行建模是不够的。 TransR/CTransR (Lin et al. 2015) 为每个关系 r 设置一个映射矩阵 Mr 和一个向量 r。在 TransR 中,h 和 t 通过矩阵 Mr 投影到关系 r 关注的方面,然后是 Mrh + r ≈ Mrt。 CTransR 是 TransR 的扩展,通过将不同的 headtail 实体对聚类成组并为每个组学习不同的关系向量。 TransR/CTransR 与之前最先进的模型相比有显着的改进。三.TransD
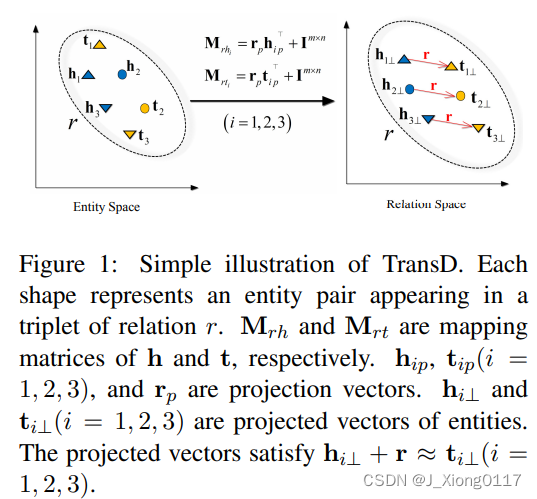
模型 在 TransD 中,每个命名符号对象(实体和关系)由两个向量表示。 第一个捕获实体(关系)的含义,另一个用于构造映射矩阵。 例如,给定一个三元组 (h, r, t),它的向量是 h, hp, r, rp, t, tp,其中下标 p 表示投影向量,h, hp, t, tp ∈ Rn 和 r, rp ∈ Rm。 对于每个三元组 (h, r, t),我们设置两个映射矩阵 Mrh,Mrt ∈ Rm×n 来将实体从实体空间投影到关系空间。 它们定义如下:
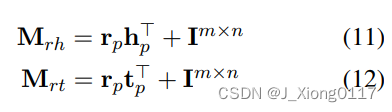
因此,映射矩阵是由实体和关系共同决定的,这种操作使两个投影向量充分交互,因为它们的每个元素都可以满足来自另一个向量每个条目。 当我们用单位矩阵初始化每个映射矩阵时,我们将 I m×n 添加到 Mrh 和 Mrh。 使用映射矩阵,我们定义投影向量如下:
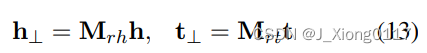
评分函数:
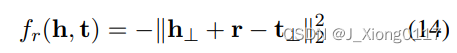
训练
假设训练集中有nt个三元组,用(hi,ri,ti)(i=1,2,…,nt) 表示第i个三元组。每个三元组有标签yi表示三元组的正负性质:

负样本生成
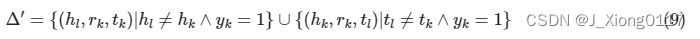
损失函数
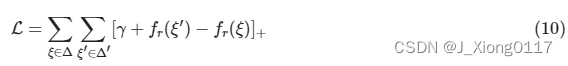
四.总结
我们引入了一个模型 TransD,将知识图嵌入到连续向量空间中以完成它们。 TransD 比 TransR/CTransR 具有更少的复杂性和更大的灵活性。 在学习命名符号对象(实体或关系)的嵌入时,TransD 会考虑它们两者的多样性。TransD可以说是TransR/CTransR的简化版本,它同时考虑了实体和关系之间的多样性,用两个向量来动态重构mapping矩阵;相比TransR/CTransR有更小的计算量,且没有矩阵运算,可以在大规模KG上应用;
-
相关阅读:
【C语言】用单链表实现一个二进制数加1的运算。
【BOOST C++ 12 函数式编程】(5) Boost.Lambda
P5117 [USACO18DEC]The Bucket List B
学习day59
Android 使用Kotlin封装RecyclerView
vue首页多模块布局(标题布局)
AWS无服务器 应用程序开发—第七章 邮件服务 发布订阅(Amazon SES)
REST风格 | Springboot | 开发风格
摄像头webrtc对讲方案之metaRTC+ZLMediaKit
基于Python是疫情期间教育领域新闻知识图谱分析
- 原文地址:https://blog.csdn.net/u013010473/article/details/126371577