图像处理之同态滤波实现灰度图像增强

一、同态滤波基本原理

同态滤波是在频域对图像增强的方法，利用滤波算法减弱低频部分，增强高频部分，来减少光照变化和使边缘锐化、细节突出。

对于图像 f(x,y) 可由照射分量 i(x,y) 和反射分量 r(x,y ) 的乘积表示，即 ：

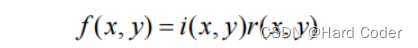
其中，i(x,y) 表示照射分量，代表描述景物照度的信息，变化较慢，可以看作是图像的低频部分； r(x,y ) 表示反射分量，代表景物细节的信息，变化较快，可以看作是图像的高频部分。

因为i(x,y) 和 r(x,y ) 是相乘的关系，首先需要对f进行对数运算，分离出与i(x,y) 和 r(x,y ) 的相关分量，从而才能对其进行傅里叶变换和频域处理。即令：

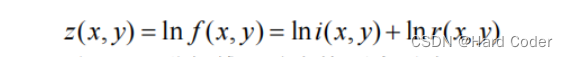
对 z(x,y) 进行傅里叶变化可表示为：

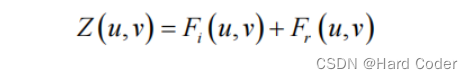
然后对 Z(u,v) 进行高通滤波处理，在频域即为 Z(u,v) 与高通滤波函数 H(u,v) 相乘：

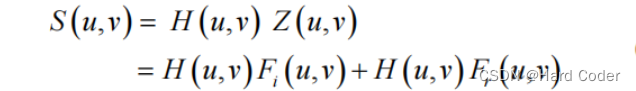
由于高通滤波器会抑制低频部分，则滤波后会提取出高频部分 r(x,y ) 对应的对数频域分量，再进行傅里叶逆变换，有：

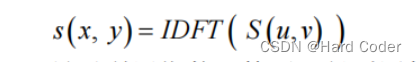
最后利用指数运算可以得到图像 g(x,y)，即为处理后的图像：

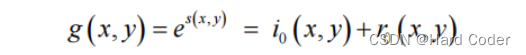
其中 i0(x,y) 和 r0(x,y) 分别为处理后的图像的照射分量和入射分量。

同态滤波算法的基本流程如下图所示：

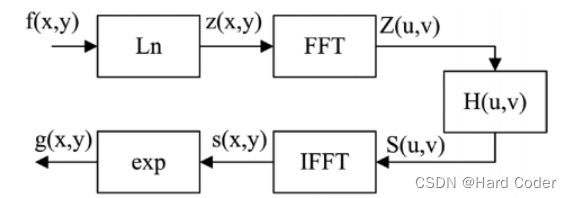
同态滤波即设置一个滤波器H(u,v)，使用不同的可控方法来影响低频分量和高频分量对图像的影响。在进行同态滤波时，关键是选择合适的H(u,v)。我们通常使用以高斯高通滤波器为模板改造的同态滤波器：

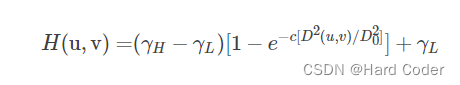
其中c为一个常数用于控制坡度的锐利度，在rL和rH之间过渡。当 rL和 rH选定，并且有rL<1且 rH>1，则该滤波器函数趋近于衰减低频（照射）的贡献，而增强高频反射的贡献，最终结果是同时进行动态范围的压缩和对比度的增强，对应的剖面图为：

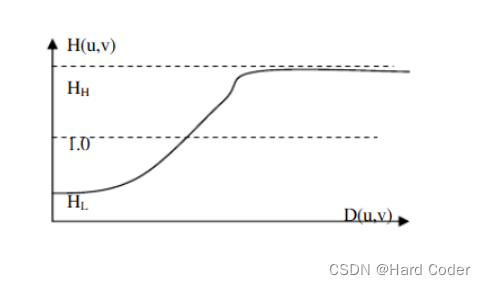
二、同态滤波实现灰度图像增强

1、实现代码
（1）homomorphicfiltering.m

% 同态滤波器
% ImageIn   -   进行滤波的输入灰度图像(若输入RGB图像需要先利用rgb2gray函数转换成灰度图像)
% High      -   高频增益,取值大于1
% Low       -   低频增益,取值在0和1之间
% C         -   锐化系数
% D0        -   截止频率(越大图像越亮)
% ImageOut  -   滤波后的输出灰度图像
function [ImageOut] = homomorphicfiltering(ImageIn, High, Low, C, D0)
    I = double(ImageIn);        % 将图像类型转换为双精度型,不会改变数据本身便于进行傅里叶变换
    [M,N] = size(ImageIn);      % 返回输入图像行数和列数
    a = floor(M / 2);           % 中心点坐标
    b = floor(N / 2);
    LogImg = log(I + 1);        % 对输入图像取对数
    Log_FFT = fft2(LogImg);    
    D=zeros(M,N);               % 初始化中间变量D和H
    H=zeros(M,N);
    for i = 1 : M 
        for j = 1 : N 
            D(i,j)=sqrt((i - a)^2 + (j - b)^2);                                           %   频率点(i,j)到频率中心的距离
            H(i, j)=(High - Low) * (1 - exp(-C * (D(i,j)^2 / (D0 ^2)))) + Low;            %   同态滤波器函数
        end 
    end
    H = ifftshift(H);                   %   对H做反中心化                             
    Log_FFT = H.* Log_FFT;              %   滤波，矩阵点乘                                                
    Log_FFT = ifft2(Log_FFT);           %   反傅立叶变换 
    ImageOut = real(exp(Log_FFT)-1);    %   取指数 
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

（2）main.m

close all;
clear all;
clc;
I=imread('night.png');
I=rgb2gray(I);
[H,W]=size(I);
rH=2;
rL=0.2;
C=2;
D0=max(H,W);
J=homomorphicfiltering(I,rH,rL,C,D0);
subplot(2,2,1);imshow(I);title('原始图像');
subplot(2,2,2);imshow(J);title('同态滤波后的图像');
subplot(2,2,3);imhist(I);title('原始图像直方图');
subplot(2,2,4);imhist(J);title('同态滤波后的图像直方图');
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

注意参数的设置：对于偏暗图像的增强的各参数配置为rH=2,rL=02,C=0.1,D0=max(H,W)（例如本例）。

2、实现效果

（1）原始RGB图像

（2）同态滤波后的图像

参考博客：
（1）经典的同态滤波算法的优化及其应用参数配置
（2）【图像增强】基于高斯同态滤波实现图像增强附matlab代码
（3）基于MATLAB对低照度图像进行直方图均衡化和同态滤波操作

虽然简单实现了同态滤波对灰度图像增强，但是我还存在不少疑问：
（1）灰度图像对应二维矩阵比较容易实现，但是RGB图像对应三维矩阵，其图像增强的操作还不知道如何实现。
（2）对于这段处理代码理解不是很透彻，因为我看到好多人第一行代码没有使用sqrt函数，第二行代码是以高斯高通滤波器变换而来，为什么分母没有除于2*D0^2 而是除于 D0^2以及该公式如何推导得出。

（3）通过对同态滤波实现灰度图像增强的研究，发现还有很多图像增强的算法有待学习。