决策树(Decision tree)基本原理与基于scikit-learn的实现

决策树（Decision tree,DT）是一类常见的机器学习方法，属于监督学习的一种。它通过给定的训练数据，计算各种情况发生的概率，在此基础上选择合适的划分并构造决策树，用于数据类别的预测判断，同时也可以进行数据的拟合回归。

（一）理论基础

（1）基本模型

设一个数据集有p个指标(属性)[1,2,..,p]，指标i中的值种类个数pi(各个指标内的值个数不一定相同)，种类数为n。决策树的形式大致为：

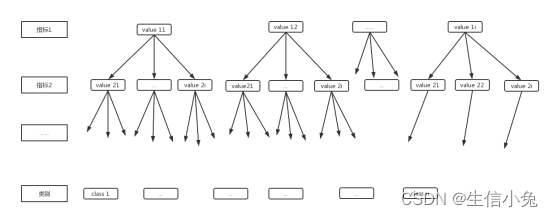
上图为了表示简便，决策树从上到下依次按指标1，2...划分。利用这样的一个决策树，我们可以判断任意给定的数据所属类别。例如，一个数据指标1的值为value12，指标2的值为value22......我们在决策树从上到下依次寻找，直到最后的叶节点，所得类别即为该数据所属类别。

然而，在实际问题中，很多时候我们所遇到的数据并不都是离散的值，而是连续的数值。对于连续属性，可采用离散属性离散化技术——例如将数从小到大排列，用若干划分点把数据分成若干部分，其中最简单的策略是采用二分法(bi-partition)进行处理(C4.5决策树算法采用该方法)。

所以，构造决策树的关键在于如何选择最优划分属性，即应该按照怎样的指标顺序依次划分数据，对于连续属性，我们还要确定划分点。

（2）构造方法

对于给定的数据集，我们首先需要确定数据集划分，划分数据集的原则是：将无序的数据变得更加有序。实现该方法可以采用信息论度量信息。在这里兔兔先介绍所用到的相关概念。

信息熵(information entropy)：度量样本集合纯度的一种常用指标，也成为香农熵(shannon entorpy)。值越小，信息纯度越高。

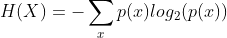
其中X表示数据样本，x为X中的可能取值，p(x)表示x发生(出现)的概率。在本文所研究的问题中，我们可以认为值在样本中出现的频率为概率，所以可以用x出现次数除以样本总数作为p(x)。例如，一个样本中某一指标值为[1,1,1,1,1,0,0,0,1,1,2,2]，则信息熵为:

信息增益(information gain)：描述一个属性区分数据样本的能力。

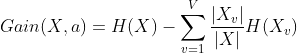
其中X表示数据样本，a表示划分的属性，该属性有V个可能取值。决策树中信息熵与信息增益的计算，信息熵部分都是计算数据中关于种类的信息熵，H(X)表示树的上一层所有数据中种类的信息熵，H(Xv)是计算属性a划分下值为v的数据中种类的信息熵。

对于上面的数据，我们可以先按照属性1进行划分。计算H(X)：

在属性1中，有两个可能取值1、2，取值为1的个数为4，该取值下类别a个数为2，b个数为2；取值为2的个数为4，该取值下类别a个数为3，b个数为1。所以信息增益中第二个部分为：

所以，信息增益为：

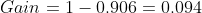
(注：这里的信息熵、信息增益的知识借用了信息论中的知识，但是与之又有所区别。在信息论中熵常用H表示，这里常用Ent；信息增益在信息论中也称为相对熵、KL散度、信息散度)。

所以，利用信息增益的方法，我们可以确定属性划分的方法，即每次计算各个属性的信息增益，选择使得信息增益最大的属性划分来划分属性，构建决策树。

对于连续属性，若采取二分法，可以将数从小到大依次排列[a1,a2,......,an]，取所有相邻的两个数的中点作为候选划分点，这样的划分点一共有n-1个。之后用各个待划分点把数据分成两个部分，计算信息增益，信息增益值最大的对应划分点即为我们所找的划分点。

（3）其它方法

除了采用信息增益(ID3决策树采用此法)寻找划分数据集的属性，也可以采用增益率(gain ratio)（C4.5决策树算法采用此法）、基尼指数(gini index)（CART决策树采用此法）等方法。

决策树通常会出现过拟合的情况，此时可以采用剪枝(pruning)的方法来处理，其基本策略有：预剪枝(prepruning)、后剪枝(postpruning)。预剪枝是在决策树生成的过程中，对每个节点在划分前先进行估计，若当前节点的划分不能带来决策树泛化能力的提升，则停止划分，标记当前节点为叶节点。后剪枝是先从训练集生成决策树，然后从下往上对非叶节点进行考察，若将该节点对应的子树替换成叶节点可以带来决策树泛化性能的提升。则将该子树替换为叶节点。

（4）算法实现

1.信息熵的计算

import numpy as np
def entropy(dataset):
    n=len(dataset)#样本数
    label={} #统计各类的个数
    for data in dataset:
        if data[-1] not in label.keys(): #数据类别在每行最后一列
            label[data[-1]]=0
        label[data[-1]]+=1
    ent=0
    for key in label:
        p=label[key]/n
        ent+=-p*np.log2(p)
    return ent
a=[[1,2,'a'],
   [2,3,'a'],
   [3,4,'b']]
print(entropy(a)) #以a为例计算香农熵

2.由某一属性a划分数据

def splitDataset(dataset,a,value):
    '''dataset:数据样本
    a:属性，这里是数据中的第a列
    value:属性a中的某一取值value
    '''
    newdataset=[]#划分之后的数据
    for data in dataset:
        if data[a]==value: #判断数据中该属性第data个值是否为value
            newdata=data[0:a]
            newdata.extend(data[a+1:]) #抽取除属性a的数据
            newdataset.append(newdata)
    return newdataset

print(splitDataset(a,a=0,value=1))
'''-----------------------------'''
>>>[[2, 'a']]

3.由信息增益确定数据集划分

def choosefeature(dataset):
    nf=len(dataset[0])-1 #样本属性个数
    baseEnt=entropy(dataset) #信息增益中的第一部分
    bestinfogain=0
    for i in range(nf):
        featueList=[data[i] for data in dataset] #属性i的所有数据
        value=set(featueList) #属性i中所有可能取值集合
        newEnt=0 #信息增益的第二部分
        for v in value:
            subDataset=splitDataset(dataset,i,v)
            p=len(subDataset)/len(dataset)
            newEnt+=p*entropy(subDataset)
        infogain=baseEnt-newEnt #计算利用属性i划分的信息增益
        if infogain>bestinfogain:
            bestinfogain=infogain #选择最大的信息增益
            bestfeature=i #选择最大信息增益下的属性
    return bestfeature

4.构建决策树

def majority(classList):
    '''选择classList中个数最多的那个值'''
    classdict={}
    for c in classList:
        if c not in classList:
            classdict[c]=0
        classdict[c]+=1
    a=max(classdict.values())
    for key,item in classdict.items():
        if item==a:
            return key
def creatTree(dataset,featureLabel):
    '''dataset:数据集
    featureLabel:各属性的标签'''
    classList=[data[-1] for data in dataset] #样本类别
    if classList.count(classList[0])==len(classList):
        return classList[0] #若划分完全后叶节点所有值相同，停止划分返回该值
    if len(dataset[0])==1:
        return majority(classList) #若已经划分完，返回该叶节点中值个数最多的那个值
    bestfeature=choosefeature(dataset) #选择划分
    bestfeatueLabel=featureLabel[bestfeature] #该划分属性的标签
    Tree={bestfeatueLabel:{}}
    del (featureLabel[bestfeature]) #去掉已划分的属性标签
    value=[data[bestfeature] for data in dataset] #选取该属性的值
    valueSet=set(value)
    for v in valueSet:
        subLabel=featureLabel
        Tree[bestfeatueLabel][v]=creatTree(splitDataset(dataset,bestfeature,v),subLabel) #递归创建树
    return Tree

print(creatTree(a,featureLabel=['feature1','feature2']))
'''---------------------------------------------------'''
>>>{'feature1': {1: 'a', 2: 'a', 3: 'b'}}

（二）决策树分类

（1）基本方法

在sklearn中，可以利用DecisionTreeClassifier()来实现。

from sklearn import tree
Tree=tree.DecisionTreeClassifier()
traindata=[[11,23],
   [34,22],
   [55,66],
   [3,1],
   [444,24]]
trainlabel=[1,1,2,2,3]
Tree.fit(traindata ,trainlabel)
yp=Tree.predict([[11,22]])
print(yp)

在DecisionTreeClassifer()中，有以下参数：

criterion：衡量属性划分质量。'gini'基尼指数；'log_loss'或'entropy'香农信息增益;

splitter：用于在每个节点选择拆分策略。'best'最佳拆分；'random'随机拆分。

max_depth：树的最大深度。默认为None,树一直扩展到叶节点全为同一类别数据或包含少于min_samples_split样本。

min_samples_split：拆分内部节点所需的最小样本数。

min_samples_leaf：叶节点所需最小样本数。

min_weight_fraction_leaf：需要位于叶节点的权重总和，即所有输入样本的最小加权分数，默认样本具有相同的权重。

max_features：寻找最佳分割时要考虑的特征数量。

max_leaf_nodes：以最佳优先方式使用‘max_leaf_nodes’生成决策树。

random_state:控制估计器estimator随机性。

min_impurity_decrease：若此拆分的不纯度减少大于等于此值，则该节点被拆分。

ccp_alpha：最小成本复杂度修剪，决策树剪枝，默认不剪枝。

（2）决策树图绘制

在训练好决策树后，可以采用plot_tree()画决策树图。

from sklearn import tree
import pandas as pd
data=pd.DataFrame(pd.read_csv('Dry_Bean_Dataset.csv'))
x=data.loc[:,'Area':'ShapeFactor4']
y=data.loc[:,'Class']
Tree=tree.DecisionTreeClassifier()
Tree.fit(x,y)
tree.plot_tree(Tree)
plt.show()

 当然，我们也可以设置树的深度。例如，我们让树的最大深度max_depth=10。则树图为：

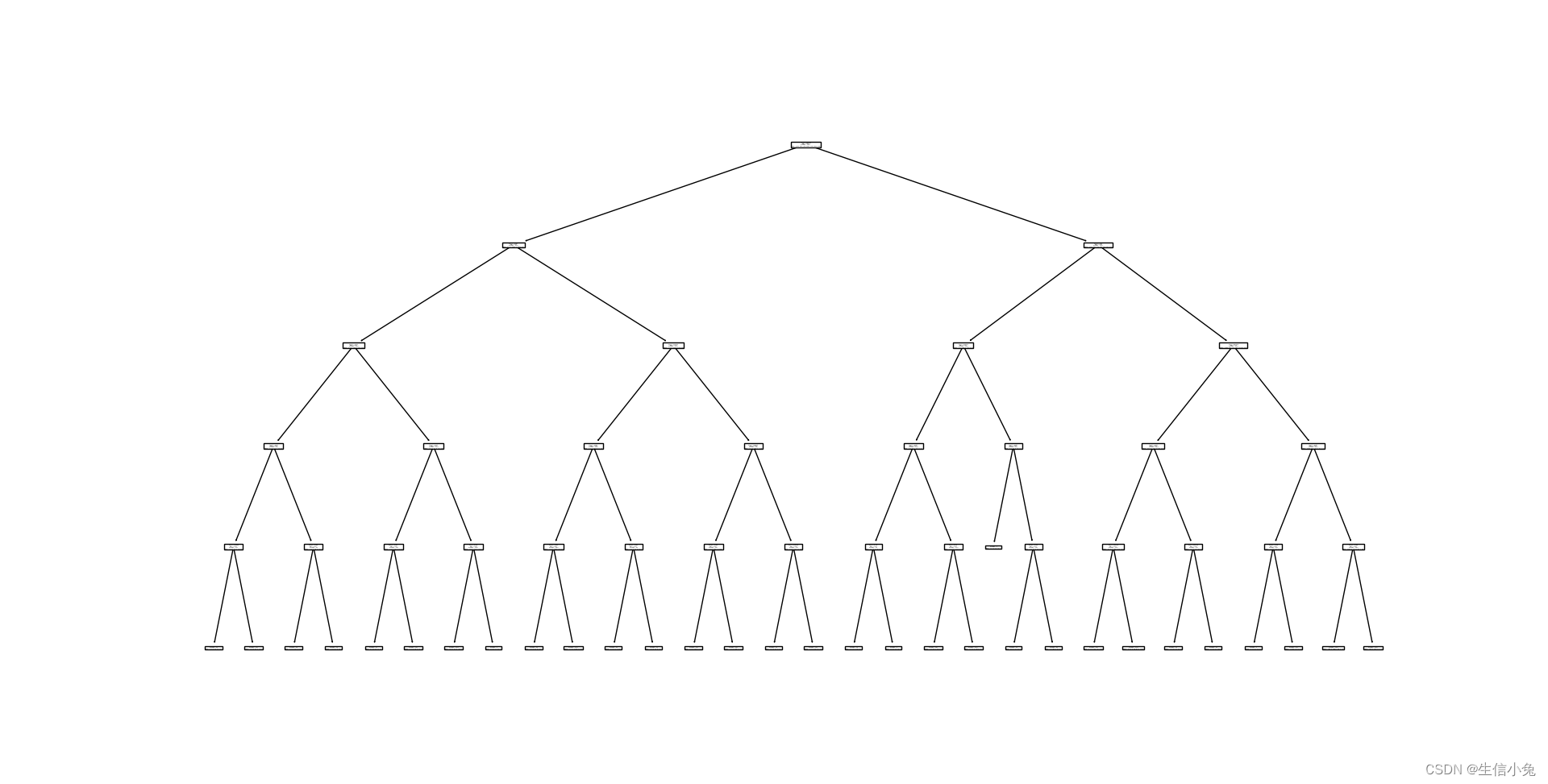
在plot_tree()中，有以下参数：

max_depth：树的最大深度，若为None,生成完全树，默认为None。

feature_names：每个特征的名，参数值为各个特征的名组成的列表。

class_names：每个目标类的名称，True为显示名称，默认False。

labels：是否显示一些信息标签。'all'显示每个节点；'root'只显示根节点；'none'不显示任何节点，默认为'all'。

impurity：是否显示不纯度，默认为True。

node_ids：是否显示每个节点的ID号，True表示显示，默认False。

filled：图形是否填充颜色，默认False。

rounded：若为True，绘制圆角节点并使用Helvetica。默认False。

fontsize：字体大小。

ax：要绘制到的轴(与matplotlib结合，例如绘制子图时可以使用，将ax轴传给ax)。

tree.plot_tree(Tree,max_depth=2,feature_names=data.columns,class_names=True,label='all',rounded=True,fontsize=10,filled=True,
               proportion=True,impurity=True,node_ids=True)
plt.show()

（三）决策树回归

（1）基本方法

在sklearn中，决策树回归用DecisionTreeRegressor()来实现。

from sklearn import tree
Tree=tree.DecisionTreeRegressor()
x=np.linspace(0,10,90)
y=np.sin(x)
x=np.reshape(x,(-1,1))
Tree.fit(x,y)
 
testx=np.linspace(0,10,100)
testx=np.reshape(testx,(-1,1))
 
yp=Tree.predict(testx)
'''score=Tree.score(x,y)
print(score)'''
plt.scatter(x,y,color='red')
plt.plot(testx,yp,color='green')
plt.show()

运行结果如下：

在DecisionTreeRegressor()中的参数与前面DecisionTreeRegession()中的参数基本相同，但是也有不同之处。

criterion：默认'squared_error'均方误差；'absolute_error'平均绝对误差；'friedman_mse'弗里德曼；'poisson'泊松偏差。

（四）总结

本文通过决策树的基本概念，以信息增益的划分方法为例阐述分类决策树的原理，并采用sklearn来实现决策树分类与树回归。实际上决策树的内容较为广泛，方法众多，并且针对过拟合的情况有各种剪枝处理，如预剪枝、后剪枝等。