1. 方案设计目标

学习A*路径规划算法，优化启发函数，并在ROS中进行测试。

2. 技术指标

安装Linux系统，建议Ubuntu18.04；
安装ROS环境并学习其基本操作；
查找A路径规划资料，学习并熟知A路径规划算法；
对比赛中所提供A*算法的启发函数AstarPathFinder::getHeu( )代码进行优化或改进并编写代码，此次比赛中提供了三种基本启发函数代码：曼哈顿距离、对角距离和欧几里得距离，可以任选一种进行改进，或者选择其他更优的启发函数。

3. 主要研究内容

3.1 A*算法的思想与原理

在我们以往学习到的路径寻找中，我们可以想到广度优先搜索（BFS：Breadth First Search）和深度优先搜索（DFS：Depth-First-Search） 进行路径寻找。先看一下广度优先搜索如下图。BFS以起点A为圆心，先搜索A周围的所有点，形成一个类似圆的搜索区域，再扩大搜索半径，进一步搜索其它没搜索到的区域，直到终点B进入搜索区域内被找到。如图3-1所示：

图3-1
再看一下深度优先搜索，这里的深度优先搜索不是所有路径都搜索而是沿着B点方向搜索。DFS则是让搜索的区域离A尽量远，离B尽量近，比如现在你在一个陌生的大学校园里，你知道校门口在你的北方，虽然你不知道你和校门口之间的路况如何，地形如何，但是你会尽可能的往北方走，总能找到校门口。如图3-2所示：

图3-2
比起BFS，DFS因为尽量靠近终点的原则，其实是用终点相对与当前点的方向为导向，所以有一个大致的方向，就不用盲目地去找了，这样，就能比BFS能快地找出来最短路径，但是这种快速寻找默认起点A终点B之间没有任何障碍物，地形的权值也都差不多。如果起点终点之间有障碍物，那么DFS就会出现绕弯的情况。如图3-3所示

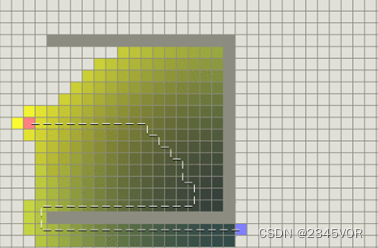
图3-3
图中DFS算法使电脑一路往更右下方的区域探索，可以看出，在DFS遇到障碍物时，其实没有办法找到一条最优的路径，只能保证DFS会提供其中的一条路径（如果有的话）。大概了解了BFS和DFS，对比这两者可以看出来，BFS保证的是从起点到达路线上的任意点花费的代价最小（但是不考虑这个过程是否要搜索很多格子）；DFS保证的是通过不断矫正行走方向和终点的方向的关系，使发现终点要搜索的格子更少（但是不考虑这个过程是否绕远）。
A算法的设计同时融合了BFS和DFS的优势，既考虑到了从起点通过当前路线的代价（保证了不会绕路），又不断的计算当前路线方向是否更趋近终点的方向（保证了不会搜索很多图块），是一种静态路网中最有效的直接搜索算法。A算法运用的是估价思想。查找过程：在待遍历列表中（刚开始只有点A），我们在列表中查找一个估价（当前点到终点距离估价，后续会讲）最小的点（k），对点k进行一次广度优先查找，也就是它移动一次到底的下一个坐标（右，右上，上，左上，左，左下，下，右下）不包含已经遍历过的点和不能到达的点，将能查找的点添加到队列中，并将点K从队列中移除。重复1、2步骤直到到底B点，或者队列已经为空说明没有路径可以到达点B。
运用的思想：
先进行一次DFS搜索再进行一次BFS搜索，循环这个过程直到找到目标点B。
过程1：运用DFS思想，尽量找离B近的点（也就是估值最小的点）。
过程2：运用BFS思想，以点K为圆心，搜索A周围的所有还未搜索的点。

3.2 A*算法的计算方法

公式：F=G+H；G=从起点A移动到指定方格的移动代价，沿着到达该方格而生成的路径。我们约定直行移动一次代价10，对角线的移动代价为14。（实际对角移动距离是2的平方根，或者是近似的1.414倍的横向或纵向移动代价）。H=从指定的方格移动到终点B的估算成本。计算从当前方格横向或纵向移动到达目标所经过的方格数，忽略对角移动，然后把总数乘以10 。
我们设当前点为K，H值很容易计算，H=（两个点横坐标距离+两个点纵坐标距离）X 10
G值计算，计算K到A的最小估价我们只需要计算K点的周围八个点（可以被访问且已经被访问点）的g值+到K点的移动代价，其中最小估价即为K点的g值，这个点我们称为K点的父节点。k点正在访问，那么它周围至少有一个点已经被访问了。如图3-4所示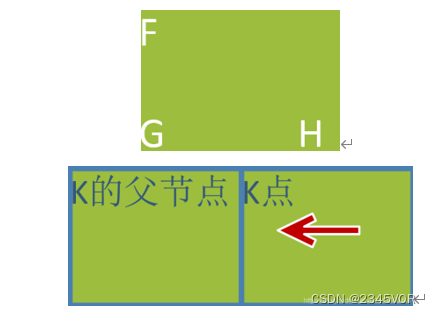

图3-4
箭头指向的是它父节点的坐标，后续找路线需要用到。
实例演示
坐标访问和父节点查找约定顺序：右，右上，上，左上，左，左下，下，右下，沿X轴增加的方向为右，沿Y轴增加的方向为上，父节点可能会有多个，这里选择代价最小最后搜索的为父节点。坐标A(2，2)，目标坐标B(6，3)，已经对坐标A进行了估值。如图3-5所示

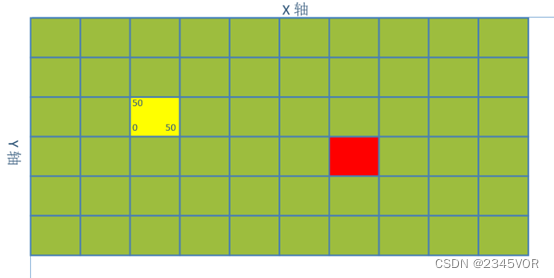
图3-5
对点（2，2）八个方向的坐标进行估值，它们的父节点都是（2，2），最小估值坐标紫色（3，3），标记紫色只是为了方便下一次寻找。估值顺序我们约定（右，右上，上，左上，左，左下，下，右下），此后我们都按照这个顺序进行。如图3-6所示：

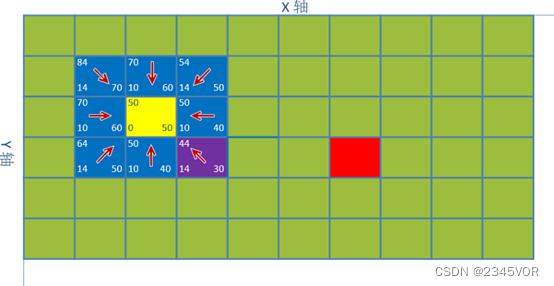
图3-6
对点（3，3）八个方向的坐标进行估值（已经估值的不用再计算），我们称已经估值的点为已经被访问，最小估值坐标紫色（4，3）。父节点搜索顺序约定（右，右上，上，左上，左，左下，下，右下），g值最小最后访问的点为父节点。如下图。这个图我们需要理解箭头是怎样确定的。例如点（4，3）它的父节点既可以是点（3，3）也可以是点（3，2），访问顺序是先访问点（3，3）后访问点（3，2）所以我们把点（3，2）作为点（4，3）的父节点。如图3-7所示

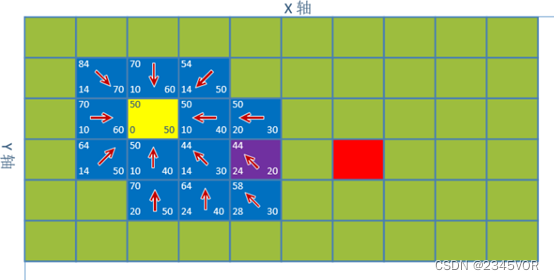
图3-7
对点（4，3）继续寻找，最小估值坐标紫色（5，3）。如图3-8所示：

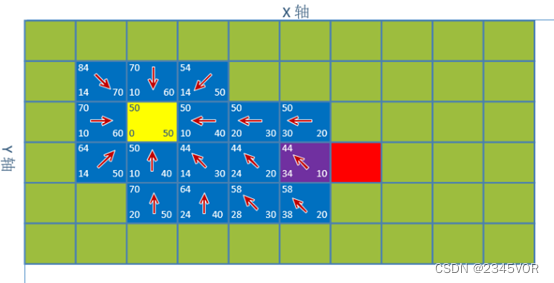
图3-8
对点（5，3）继续寻找，搜索到了终点，停止搜索。如图3-9所示：

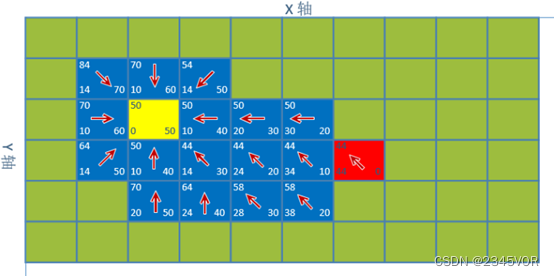
图3-9
通过终点依次查找它们的父节点直到起点，然后将坐标点逆序，就是我们要的路线了。路线：（2，2）、（3，2）、（4，2）、（5，2）、（6，3）。如图3-10所示：

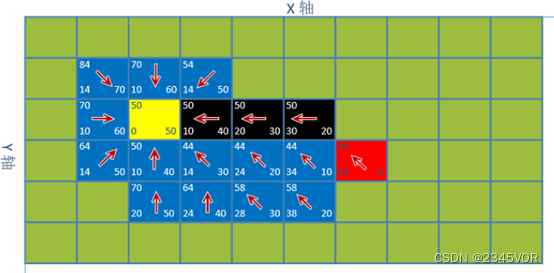
图3-10

4. 代码实现与优化

4.1 启发函数

启发式函数h\left(n\right)的确定是A*算法中的重要内容，启发式函数越准确，找到最优解的速度越快。其中常用的启发函数包括欧几里得式启发函数、曼哈顿式启发函数、对角线式启发函数。
欧几里得式启发函数
$$h(n)=\sqrt{{\left(x_n-x_{goal}\right)}^2+{\left(y_n-y_{goal}\right)}^2+{\left(z_n-z_{goal}\right)}^2}$$
其中x_i(i=n,goal)，y_i(i=n,goal)和z_i(i=n,goal)分别是节点n与终点节点在三维空间中的坐标。
曼哈顿式启发函数
$$h(n)=\left|x_n-x_{goal}\right|+\left|y_n-y_{goal}\right|+\left|z_n-z_{goal}\right|$$
对角线式启发函数

针对A算法路径不平滑、冗余拐点多的问题，许多学者提出了改进A算法，其中主要包括两类：针对代价函数的改进与针对扩展区域的改进。本次针对代价函数中的重要因素：启发函数$h\left(n\right)$，进行改进。启发式函数可以控制A的扩展节点和运行时间：（1）如果$h\left(n\right)$小于当前节点n到目标节点的实际代价则A 算法保证能找到一条最短路径。$h\left(n\right)$越小，A扩展的节点越多，运行就得越慢。（2）如果$h\left(n\right)$大于当前节点n到目标节点的实际代价，则A算法不能保证找到一条最短路径，但它的扩展节点少，运行得更快。本文在设置初始参数阶段增加了$h\left(n\right)$的权重系数W，通过调整W的大小达到动态改变代价函数$h\left(n\right)$的大小的目的，让算法可以根据具体需求进行调整。
本次程序的优化是对欧几里得启发函数的优化，优化后的公式为：
$$h\left(n\right)=W\ast \sqrt{{\left(x_n-x_{goal}\right)}^2+{\left(y_n-y_{goal}\right)}^2+{\left(z_n-z_{goal}\right)}^2}$$
在用栅格法随机生成的地图中，通过对权重W的改变，动态调整A*算法的搜索路径、扩展节点和时间。如图4-1、4-2、4-3所示：

图4-1

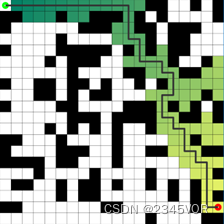
图4-2

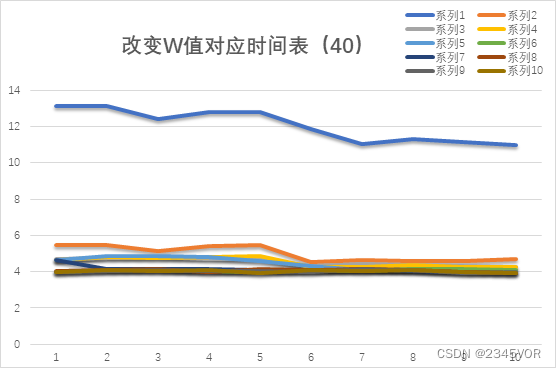
图4-3
由此我们可以看到，在改变启发函数的权重W后，对整体的规划所用时间产生的影响还是有的，特别是权重为1与大于1的数后，但是权重不是说越大越好，可以看到，在实验过程中，权重越大越趋于稳定的时间。

4.2 代码介绍

功能包结构
1

.grid_path_searcher
├── CMakeLists.txt
├── include
│   ├── Astar_searcher.h
│   ├── backward.hpp
│   └── node.h
├── launch
│   ├── demo.launch
│   └── rviz_config
│       └── demo.rviz
├── package.xml
├── src
│   ├── Astar_searcher.cpp         改进A*算法的方法
│   ├── demo_node.cpp              节点文件
│   └── random_complex_generator.cpp         生成障碍物

.waypoint_generator
├── CMakeLists.txt
├── package.xml
├── src
│   ├── sample_waypoints.h
│   └── waypoint_generator.cpp         发布目标点信息
└── waypoint_generator.txt
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

主要修改代码
1

在Astar_searcher.cpp文件下，主要对启发函数AstarPathFinder::getHeu进行修改，代码如下：

double AstarPathFinder::getHeu(GridNodePtr node1, GridNodePtr node2)
{
     double h;
    auto node1_coord = node1->coord;
    auto node2_coord = node2->coord;

    // Heuristics 1: Manhattan
    //h = std::abs(node1_coord(0) - node2_coord(0) ) +
     //    std::abs(node1_coord(1) - node2_coord(1) ) +
     //    std::abs(node1_coord(2) - node2_coord(2) );

/*对欧几里得启发函数进行优化*/
    // Heuristics 2: Euclidean
     h = weight_ * ( std::sqrt(std::pow((node1_coord(0) - node2_coord(0)), 2 )+
         std::pow((node1_coord(1) - node2_coord(1)), 2 ) +
         std::pow((node1_coord(2) - node2_coord(2)), 2 )));

    // Heuristics 3: Diagnol distance
  //  double dx = std::abs(node1_coord(0) - node2_coord(0) );
   // double dy = std::abs(node1_coord(1) - node2_coord(1) );
    //double dz = std::abs(node1_coord(2) - node2_coord(2) );
    //double min_xyz = std::min({dx, dy, dz});
   // h = dx + dy + dz + (std::sqrt(3.0) -3) * min_xyz;

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

在Astar_searcher.h文件下，对启发函数中所用到的函数名进行定义：

#ifndef _ASTART_SEARCHER_H
#define _ASTART_SEARCHER_H

#include 
#include 
#include 
#include 
#include "backward.hpp"
#include "node.h"

class AstarPathFinder
{	
	private:

	protected:
		uint8_t * data;
		
		GridNodePtr *** GridNodeMap;
				
		Eigen::Vector3i goalIdx;
		
		int GLX_SIZE, GLY_SIZE, GLZ_SIZE;
		int GLXYZ_SIZE, GLYZ_SIZE;

/*对所用到的变量名进行定义*/
                double weight;
                double weight_;
		
		double resolution, inv_resolution;
		
		double gl_xl, gl_yl, gl_zl;
		double gl_xu, gl_yu, gl_zu;

		GridNodePtr terminatePtr;
		
		std::multimap<double, GridNodePtr> openSet;
		
		double getHeu(GridNodePtr node1, GridNodePtr node2);
		
		void AstarGetSucc(GridNodePtr currentPtr, std::vector<GridNodePtr> & neighborPtrSets, std::vector<double> & edgeCostSets);		
		
    	bool isOccupied(const int & idx_x, const int & idx_y, const int & idx_z) const;
		bool isOccupied(const Eigen::Vector3i & index) const;
		
		bool isFree(const int & idx_x, const int & idx_y, const int & idx_z) const;
		bool isFree(const Eigen::Vector3i & index) const;
		
		Eigen::Vector3d gridIndex2coord(const Eigen::Vector3i & index);
		Eigen::Vector3i coord2gridIndex(const Eigen::Vector3d & pt);

	public:
		AstarPathFinder(){};
		~AstarPathFinder(){};
		
		void AstarGraphSearch(Eigen::Vector3d start_pt, Eigen::Vector3d end_pt);
		
		void resetGrid(GridNodePtr ptr);
		
		void resetUsedGrids();
		
		void initGridMap(double _resolution, Eigen::Vector3d global_xyz_l, Eigen::Vector3d global_xyz_u, int max_x_id, int max_y_id, int max_z_id);
		
		void setObs(const double coord_x, const double coord_y, const double coord_z);

		Eigen::Vector3d coordRounding(const Eigen::Vector3d & coord);
		
		std::vector<Eigen::Vector3d> getPath();
		
		std::vector<Eigen::Vector3d> getVisitedNodes();
};
对demo_node.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71

cpp文件的代码进行相关优化，通过ros::param::get函数达到通过launch文件可以灵活修改启发函数中的权重系数，也为后续进行动态权重的设计进行铺垫

int main(int argc, char** argv)
{
    ros::init(argc, argv, "demo_node");
    ros::NodeHandle nh("~");
    double weight;
    double weight_;

    _map_sub  = nh.subscribe( "map",       1, rcvPointCloudCallBack );
    _pts_sub  = nh.subscribe( "waypoints", 1, rcvWaypointsCallback );

    _grid_map_vis_pub             = nh.advertise<sensor_msgs::PointCloud2>("grid_map_vis", 1);
    _grid_path_vis_pub            = nh.advertise<visualization_msgs::Marker>("grid_path_vis", 1);
_visited_nodes_vis_pub        = nh.advertise<visualization_msgs::Marker>("visited_nodes_vis",1);

/*对权重系数进行传参*/
    ros::param::get("~weight",weight_);
    
    nh.param("map/cloud_margin",  _cloud_margin, 0.0);
    nh.param("map/resolution",    _resolution,   0.2);
    
    nh.param("map/x_size",        _x_size, 50.0);
    nh.param("map/y_size",        _y_size, 50.0);
    nh.param("map/z_size",        _z_size, 5.0 );
    
    nh.param("planning/start_x",  _start_pt(0),  0.0);
    nh.param("planning/start_y",  _start_pt(1),  0.0);
    nh.param("planning/start_z",  _start_pt(2),  0.0);

    _map_lower << - _x_size/2.0, - _y_size/2.0,     0.0;
    _map_upper << + _x_size/2.0, + _y_size/2.0, _z_size;
    
    _inv_resolution = 1.0 / _resolution;
    
    _max_x_id = (int)(_x_size * _inv_resolution);
    _max_y_id = (int)(_y_size * _inv_resolution);
    _max_z_id = (int)(_z_size * _inv_resolution);

    _astar_path_finder  = new AstarPathFinder(); 

    _astar_path_finder  -> initGridMap(_resolution, _map_lower, _map_upper, _max_x_id, _max_y_id, _max_z_id);

    ros::Rate rate(100);
    bool status = ros::ok();
    while(status) 
    {		
        ros::spinOnce();      
        status = ros::ok();
        rate.sleep();
    }
 
    delete _astar_path_finder;
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

对demo.launch文件的parmer参数文件进行配置：

<launch>

<arg name="map_size_x" default="10.0"/>
<arg name="map_size_y" default="10.0"/>
<arg name="map_size_z" default=" 2.0"/>

<arg name="start_x" default=" 0.0"/>
<arg name="start_y" default=" 0.0"/>
<arg name="start_z" default=" 1.0"/>

  <node pkg="grid_path_searcher" type="demo_node" name="demo_node" output="screen" required = "true">
      <remap from="~waypoints"       to="/waypoint_generator/waypoints"/>
      <remap from="~map"             to="/random_complex/global_map"/> 
      
      <param name="weight_" value="10" />
      <param name="map/margin"       value="0.0" />
      <param name="map/resolution"   value="0.2" />
      <param name="map/x_size"       value="$(arg map_size_x)"/>
      <param name="map/y_size"       value="$(arg map_size_y)"/>
      <param name="map/z_size"       value="$(arg map_size_z)"/>

      <param name="planning/start_x" value="$(arg start_x)"/>
      <param name="planning/start_y" value="$(arg start_y)"/>
      <param name="planning/start_z" value="$(arg start_z)"/>
  node>

  <node pkg ="grid_path_searcher" name ="random_complex" type ="random_complex" output = "screen">    
    
      <param name="init_state_x"   value="$(arg start_x)"/>
      <param name="init_state_y"   value="$(arg start_y)"/>

      <param name="map/x_size"     value="$(arg map_size_x)" />
      <param name="map/y_size"     value="$(arg map_size_y)" />
      <param name="map/z_size"     value="$(arg map_size_z)" />

      <param name="map/circle_num" value="40"/>        
      <param name="map/obs_num"    value="300"/>        
      <param name="map/resolution" value="0.1"/>        

      <param name="ObstacleShape/lower_rad" value="0.1"/>
      <param name="ObstacleShape/upper_rad" value="0.7"/>
      <param name="ObstacleShape/lower_hei" value="1.0"/>
      <param name="ObstacleShape/upper_hei" value="3.0"/>

      <param name="CircleShape/lower_circle_rad"   value="0.6"/>        
      <param name="CircleShape/upper_circle_rad"   value="2.0"/>        
      
      <param name="sensing/rate"   value="0.5"/>        
  node>

  <node pkg="waypoint_generator" name="waypoint_generator" type="waypoint_generator" output="screen">
      <remap from="~goal" to="/goal"/>
      <param name="waypoint_type" value="manual-lonely-waypoint"/>    
  node>

launch>
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

运行步骤及结果对比
运行步骤
1
2

下载并解压文件夹motionplan；创建工作空间,Ctrl+alt+t，打开终端，逐条运行下述命令；

$ mkdir -p ~/catkin_ws/src
$ cd ~/catkin_ws/src
1
2

将motionplan/src中的三个文件复制到/catkin_ws/src路径下，逐条运行下述命令；

$ catkin_init_workspace
$ cd ~/catkin_ws/ 
$ catkin_make 
$ source devel/setup.bash
$ roscore
1
2
3
4
5

重新打开一个终端，打开Rviz：

$ source devel/setup.bash
$ rviz
1
2

鼠标点击左上方file按钮，添加配置文件，配置文件路径如下，打开后显示如下页面，如图4-4、4-5所示：catkin_ws/src/grid_path_searcher/lau nch/rviz_c onfig/demo.rviz

图4-4

图4-5
打开终端逐行运行下述命令，开启launch文件，载入地图，如图4-6；

$ source devel/setup.bash 
$ roslaunch grid_path_searcher demo.launch
1
2

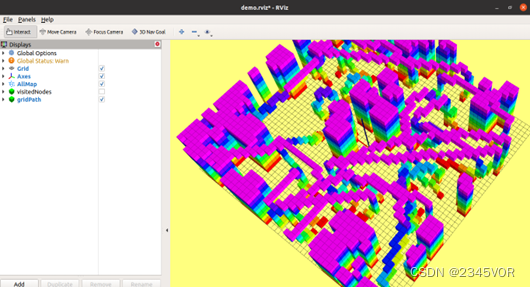
图4-6
选择3D New Goal这个图标，点击地图任意位置，出现绿色箭头，移动鼠标用于调整箭头方向，能够看到在3维地图中规划出的一条从终点到达地图中心的一条路径。
改进前后效果对比
如图4-7、4-8所示，当权重系数是1的时候（即未优化前），其路径规划所用时间为下图：

图4-7

图4-8
由此可见，整个规划时间为13ms~17ms之间，甚至会出现无法规划路径的问题。
当权重系数为3时，如下图4-9所示：

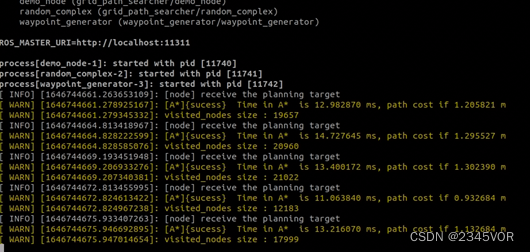
图4-9
当权重系数为10时，如下图4-10所示：

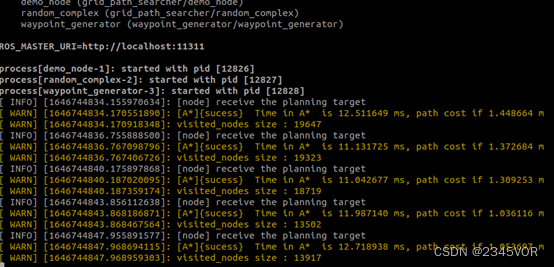
图4-10
由此看来，权重系数的适度增大对整个路径规划的成功率和效率上都有了相应的提升。

5. 后续改进与展望

后续过程中，考虑到稳点一个权重系数后，希望在针对扩展区域的改进方面，希望由4邻域扩展法进阶到8邻域和24邻域与针对代价函数的改进进行对比，目前已经进展到在MATLAB中仿真出8邻域和24邻域所用时间与路径对比，如下图5-1所示：

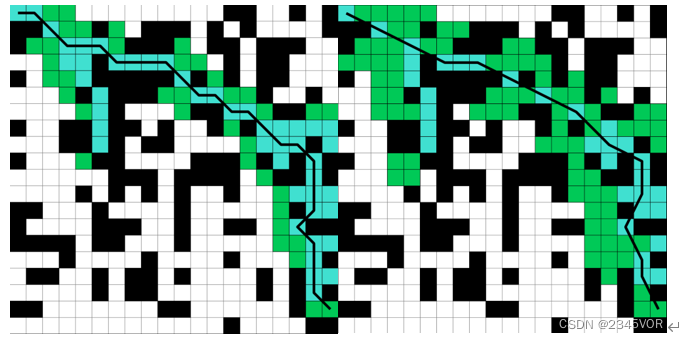
			8邻域扩展                               24邻域扩展
             图5-1
1
2

|
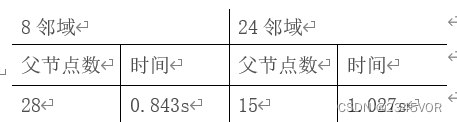
有图可以看出，邻域增多后整体的路径平滑程度有了显著的增加，但是代价就是牺牲了路径规划所用的时间，在未来的学习中，将通过不断优化改进后的A*算法，并将其应用到真实的实物上去。