大厂真题：【贪心】大疆2023秋招-矩形田地

题目描述与示例

题目描述

给定一个矩形田地，其高度为 h 且宽度为 w。同时，你将获得两个整数数组 horizontalCutting 和 verticalCutting，其中 horizontalCutting[i] 表示从矩形田地顶部到第 i 个水平切口的距离，verticalCutting[j] 表示从矩形田地的左侧到第 j 个竖直切口的距离。你的任务是根据提供的 horizontalCutting 和 verticalCutting 数组，进行水平和竖直位置的切割，并找出面积最大的那份田地，并返回其面积。

输入描述

第一行 h：田地的水平最大高度

第二行 w: 田地的垂直最大宽度

第三行horizontalCutting：数组的长度

第四行horizontalCutting：切割水平线的位置

第五行verticalCutting：数组的长度

第六行verticalCutting：切割垂直线的位置

输出描述

输出一个整数，代表切割后面积最大的田地大小。

示例

输入

5
4
3
1 2 4
2
1 3
1
2
3
4
5
6

输出

4
1

说明

输入所表示的矩形田地如下图所示，最大面积为4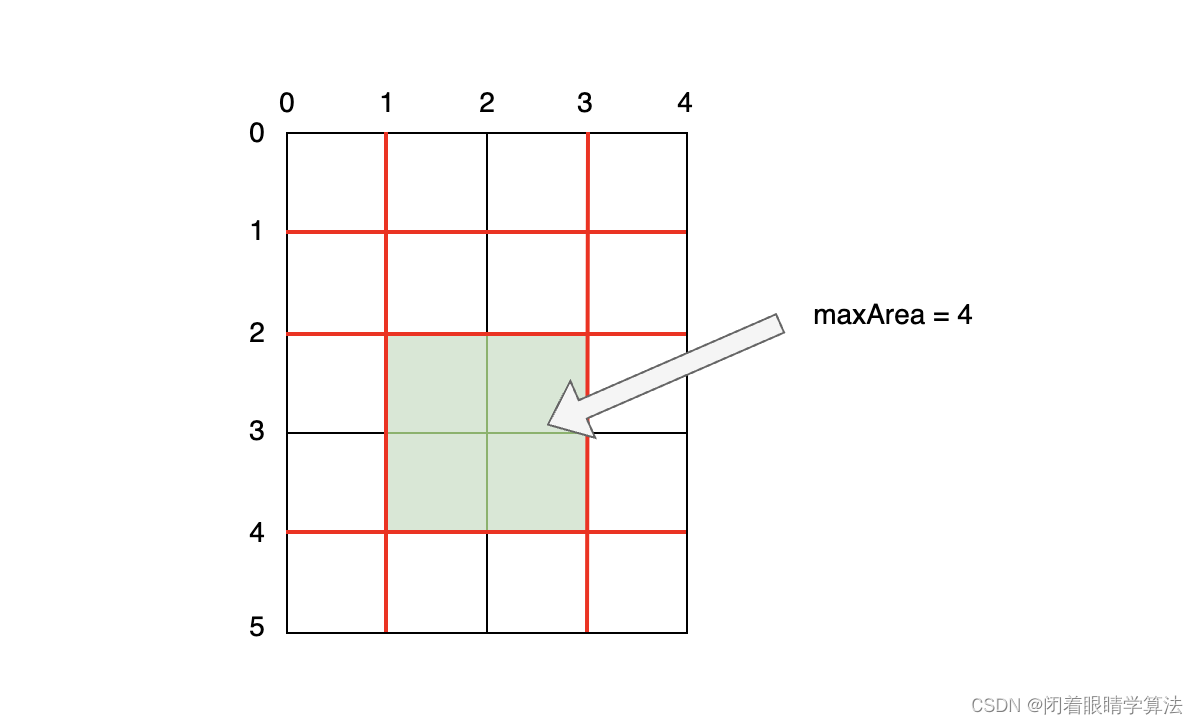

解题思路

本题思路非常直接，分别贪心地寻找x方向和y方向相隔最大的两条切割线之间的距离x_max和y_max，相乘即为答案。

代码

Python

# 题目：【贪心】大疆2023秋招-矩形田地
# 作者：闭着眼睛学数理化
# 算法：贪心
# 代码有看不懂的地方请直接在群上提问


# 输入长宽
H = int(input())
W = int(input())
# 输入y方向的切割线
yn = int(input())
y = [0] + list(map(int, input().split())) + [H]
# 输入x方向的切割线
xn = int(input())
x = [0] + list(map(int, input().split())) + [W]

# 分别对y方向和x方向，求出两个切割线之间最宽的区域
y_max = max(y[i]-y[i-1] for i in range(1, yn+2))
x_max = max(x[i]-x[i-1] for i in range(1, xn+2))
# 两者相乘，即为答案
print(y_max * x_max)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

Java

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        // Input length and width
        int H = scanner.nextInt();
        int W = scanner.nextInt();

        // Input y-direction cutting lines
        int yn = scanner.nextInt();
        int[] y = new int[yn + 2];
        y[0] = 0;
        for (int i = 1; i <= yn; i++) {
            y[i] = scanner.nextInt();
        }
        y[yn + 1] = H;

        // Input x-direction cutting lines
        int xn = scanner.nextInt();
        int[] x = new int[xn + 2];
        x[0] = 0;
        for (int i = 1; i <= xn; i++) {
            x[i] = scanner.nextInt();
        }
        x[xn + 1] = W;

        // Calculate the maximum width between the cutting lines in the y-direction
        int y_max = 0;
        for (int i = 1; i < y.length; i++) {
            y_max = Math.max(y_max, y[i] - y[i - 1]);
        }

        // Calculate the maximum width between the cutting lines in the x-direction
        int x_max = 0;
        for (int i = 1; i < x.length; i++) {
            x_max = Math.max(x_max, x[i] - x[i - 1]);
        }

        // Calculate the result by multiplying the maximum widths in both directions
        int result = y_max * x_max;
        System.out.println(result);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

C++

#include 
#include 

using namespace std;

int main() {
    int H, W;
    cin >> H >> W;

    int yn;
    cin >> yn;
    vector<int> y(yn + 2);
    y[0] = 0;
    for (int i = 1; i <= yn; i++) {
        cin >> y[i];
    }
    y[yn + 1] = H;

    int xn;
    cin >> xn;
    vector<int> x(xn + 2);
    x[0] = 0;
    for (int i = 1; i <= xn; i++) {
        cin >> x[i];
    }
    x[xn + 1] = W;

    int y_max = 0;
    for (int i = 1; i < y.size(); i++) {
        y_max = max(y_max, y[i] - y[i - 1]);
    }

    int x_max = 0;
    for (int i = 1; i < x.size(); i++) {
        x_max = max(x_max, x[i] - x[i - 1]);
    }

    int result = y_max * x_max;
    cout << result << endl;

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

时空复杂度

时间复杂度：O(N+M)。N和M分别是horizontalCutting 和 verticalCutting的大小。

空间复杂度：O(1)。仅需若干常数变量。

---

华为OD算法/大厂面试高频题算法练习冲刺训练

• 华为OD算法/大厂面试高频题算法冲刺训练目前开始常态化报名！目前已服务100+同学成功上岸！

• 课程讲师为全网50w+粉丝编程博主@吴师兄学算法 以及小红书头部编程博主@闭着眼睛学数理化

• 每期人数维持在20人内，保证能够最大限度地满足到每一个同学的需求，达到和1v1同样的学习效果！

• 60+天陪伴式学习，40+直播课时，300+动画图解视频，300+LeetCode经典题，200+华为OD真题/大厂真题，还有简历修改、模拟面试、专属HR对接将为你解锁

• 可上全网独家的欧弟OJ系统练习华子OD、大厂真题

• 可查看链接 大厂真题汇总 & OD真题汇总(持续更新)

• 绿色聊天软件戳 od1336了解更多