矩阵分析与应用+张贤达

第四章（一）

1. 矩阵分解的分类

矩阵分解
所谓矩阵的分解(decomposition或factorization)，就是通过线性变换，将某个给定或已知的矩阵分解为二个或三个矩阵标准型的乘积(个别情况下分解为两个矩阵标准型之和)。

虽然矩阵的分解有十几种之多，看似零乱，但是它们之间实则有着明显的类属。在这里，我们主要根据矩阵分解后得到的矩阵的标准型以及是对单个矩阵还是两个矩阵组成的矩阵束或矩阵对进行分解来划分矩阵的分解类别。

1.1 单个矩阵的分解

根据矩阵 $A$ 分解后的矩阵的标准型，可分为以下四大类。
(1)对角化分解
这类分解是通过正交变换，将矩阵 $A$ 对角化的，包括以下三种形式。

奇异值分解(SVD): $A=U\Sigma V^H$ 或 $U^HAV=\Sigma$ ，其中， $U$ 和 $V$ 二者为酉矩阵， $\Sigma$ 为对角矩阵(针对一般矩阵的对角化分解)。
特征值分解(EVD): $A^HA=V\Sigma V^H$ 或 $AA^H=U\Sigma U^H$ (针对对称矩阵的对角化分解)。
CS分解:可看作是正交矩阵分块的同时对角化分解。

(2)三角化分解
这类分解将矩阵 $A$ 分解为正交矩阵三角矩阵之积，或分解为一个上三角矩阵一个下三角矩阵之积，主要有以下一种形式:

Cholesky分解: $A=GG^T$ ，其中， $G$ 为下三角矩阵(针对对称正定矩阵的三角化分解)。
QR分解: $A = QR$ 或 $Q^TA=R$ ，其中， $Q$ 是正交矩阵，而 $R$ 是上三角矩阵(针对一般矩阵的三角化分解)。
LU分解: $A = LU$ ，其中， $L$ 是单位下三角矩阵，而 $U$ 是上三角矩阵(针对非奇异矩阵的三角化分解)。

(3)三角-对角化分解
将矩阵分解为三个矩阵标准型(两个三角矩阵和一个对角矩阵)之积，或分解为两个矩阵标准型(对角矩阵和上三角矩阵)之和。这类分解有以下形式。

$LDM^T$ 分解: $A=LDM^T$ ，其中， $L$ 和 $M$ 为单位下三角矩阵，而 $D$ 为对角矩阵(针对非对称矩阵的三角-对角化分解)。
$LDL^T$ 分解: $A=LDL^T$ (针对对称矩阵的三角-对角化分解)。
Schur分解: $Q^HAQ=D+N$ ，其中， $Q$ 是酉矩阵， $D$ 是对角矩阵，而 $N$ 是严格上三角矩阵(针对复矩阵的三角-对角化分解)。

(4)三对角化分解
Householder三对角化分解: $H^TAH=T$ ，其中， $H=H_1H_2…H_{n-2}$ 为House holder变换之积，且 $T$ 是三对角矩阵。

1.2 矩阵束的分解

矩阵束的分解主要用于求解矩阵束的广义特征值分解(GEVD)问题 $Ax=\lambda Bx(x\neq 0)的QZ$ 方法中，它涉及两个矩阵的同时分解。这类分解的主要形式是广义Schur分解。

广义Schur分解: $Q^HAZ=T$ 和 $Q^HBZ=S$ ，其中， $Q$ 和 $Z$ 为酉矩阵，而 $T$ 和 $S$ 为上三角矩阵。

实现广义Schur分解需要先使用Hessenberg三对角化分解: $Q^TAZ=H$ 和 $QTBZ = T$ ，其中， $Q$ 和 $Z$ 为正交矩阵， $H$ 为上Hessenberg矩阵，而 $T$ 是上三角矩阵。
更形象些，我们可以把矩阵分解的上述各种类型画成图4.41所示的矩阵分解树(呈平躺形式)。
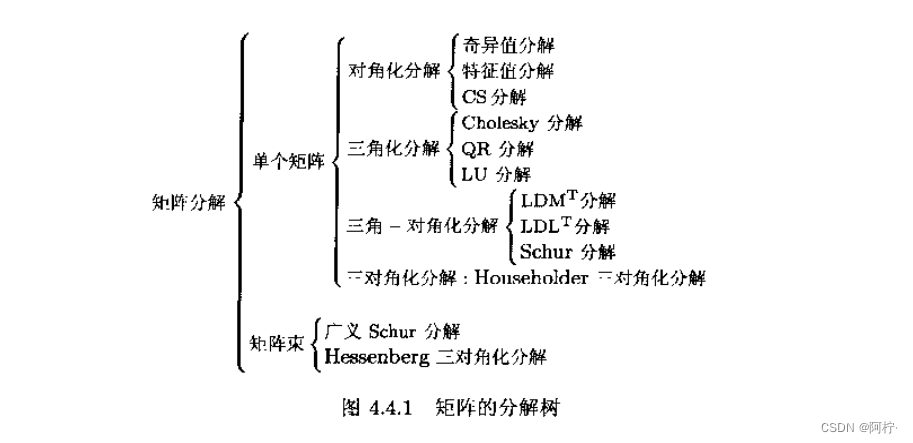
在这里插入图片描述

2. 对角化分解

任意矩阵的奇异值分解和对称矩阵的特征值分解是工程中应用最广泛的两种矩阵分解。

奇异值分解有多种推广，例如两个矩阵乘积的奇异值分解和矩阵束的广义奇异值分解等。
特征值分解也有一种以矩阵束为对象的推广即广义特征值分解。

定理 CS分解
若 $(k+j)\times (k+j)$ 矩阵

[\begin{matrix} Q_{11} & Q_{12} \\ Q_{21} & Q_{22} \end{matrix}]

Q = [Q_{11} Q_{21} Q_{12} Q_{22}]

是正交的，其中，

Q_{11}

是

k\times k

矩阵，并且

k \geq j

;则存在正交矩阵

U_1,V_1 \in R^{k\times k}

和正交矩阵

U_2,V_2 \in R^{j\times j}

使得

[\begin{matrix} U_{1} & O \\ O & U_{2} \end{matrix}]

其中

C=diag(c_1,c_2,···,c_j), c_i=cos\theta_i

S=diag(s_1,s_2,···,s_j), s_i=sin\theta_i

且

0≤\theta_1≤\theta_2≤…·≤\theta_j≤\pi/2

.
粗略地讲，

CS

分解相当于将一个正交矩阵的各个分块同时对角化。
例
矩阵

[\begin{matrix} - 0.761 & - 0.698 & - 0.006 \\ 0.548 & - 0.555 & - 0.626 \\ 0.433 & - 0.451 & 0.780 \end{matrix}]

是正交的。因此，选择正交矩阵

[\begin{matrix} 0.999 & - 0.010 & 0.000 \\ - 0.010 & - 0.999 & 0.000 \\ 0.000 & 0.000 & 1.000 \end{matrix}]

[\begin{matrix} - 0.721 & - 0.692 & 0.000 \\ - 0.692 & 0.721 & 0.000 \\ 0.000 & 0.000 & 1.000 \end{matrix}]

则有

[\begin{matrix} 1.000 & 0.000 & 0.000 \\ 0.000 & 0.780 & 0.625 \\ 0.000 & - 0.625 & 0.780 \end{matrix}]

换言之，在定理中相当于取

k = 2, j = 1

，并且

c_1=0.780，s_1=0.625

。

3. Cholesky分解

Cholesky分解
设 $A=[a_{ij}] \in R^{n\times n}$ 是对称正定矩阵， $A=GG^T$ 称为矩阵 $A$ 的Cholesky分解，其中， $G\in R^{n\times n}$ 是一个具有正的对角线元素的下三角矩阵，即

[\begin{matrix} g_{11} & 0 \\ g_{21} & g_{22} \\ ⋮ & ⋮ & ⋱ \\ g_{n 1} & g_{n 1} & \dots & g_{n n} \end{matrix}]

G = ⎣ ⎡ g_{11} g_{21} ⋮ g_{n 1} g_{22} ⋮ g_{n 1} ⋱ \dots 0 g_{nn} ⎦ ⎤

比较

A=GG^T

两边，易得

a_{ij}=\sum_{k=1}^jg_{jk}g_{ik}

从而有

g_{jj}g_{ij}=a_{ij}-\sum_{k=1}^{j-1}g_{jk}g_{ik}=v(i) \tag{1}

如果知道了 $G$ 的前 $j - 1$ 列，那么 $v (i)$ 就是可计算的。
在上式中令 $i = j$ ，立即有 $g_{jj}^2=v(j)$ 。然后，由上式得
$g_{ij}=v(i)/g_{jj}=v(i)/\sqrt{v(j)} \tag{2}$
总结以上讨论，可得到计算Cholesky分解的下述MATLAB算法
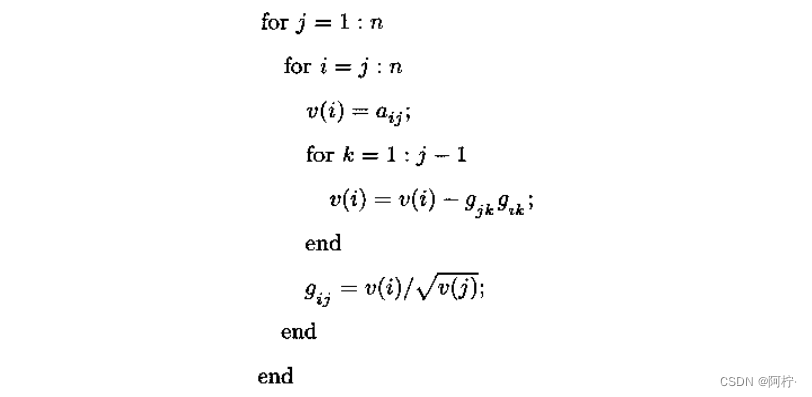
在这里插入图片描述
这一算法叫做Gaxpy Cholesky算法。Gaxpy意即广义的saxpy，而“saxpy”是在软件包LINPACK中被定义的术语，它是“标量ax+y”的英文(scalar alpha x plus y)缩写。
saxpy运算定义为
$z=\alpha x+y \Rightarrow x_i=\alpha x_i+y_i$
而Gaxpy运算系指矩阵运算 $z = A x + y$ 。
以上分析结果可以归纳为下面的定理。
定理 Cholesky分解
如果 $A\in R^{n\times n}$ 是对称正定矩阵，则Cholesky分解 $A=GG^T$ 是唯一的，其中，下三角矩阵 $G\in R^{n\times n}$ 的非零元素由(2)式决定。

下三角矩阵 $G$ 称为Cholesky三角。另外，Cholesky分解也谓之平方根方法，因为下三角矩阵 $G$ 可以视为矩阵 $A$ 的“平方根”。
一个非奇异矩阵 $A$ 的逆矩阵 $A^{-1}$ 可以通过Cholesky分解求得，即有
$A^{-1}=G^{-T}G^{-1}$
其中， $G^{-T}=(G^T)^{-1}$ 。
例
考虑利用Cholesky分解求解矩阵方程 $A x = b$ 。由于
$G^{-1}Ax =G^{-1}b\Rightarrow G^Tx=h$
其中， $h=G^{-1}b$ ，或等价为 $G h = b$ 。比较 $G h = b$ 两边的向量元素，易得向量 $h$ 的元素 $h_i$ 的递推计算公式如下:
$h_1=b_1/g_{11}$
$h_i=\frac{1}{g_{ii}}(b_i-\sum_{k=1}^{i-1}g_{ki}h_k), i=2,3,…,n$

现在，方程 $A x = b$ 的解等价为 $G^Tx=h$ 的解。注意到 $G^T$ 为上三角矩阵，因此 $x$ 可以利用熟知的回代法求出:
$x_n=h_n/g_{nn}$
$x_i=\frac{1}{g_{ii}}(h_i-\sum_{k=1}^{n-i}g_{i+k,i}x_{i+k}),i=n-1,n-2,...,1$

相关阅读:
通过webpack创建并打包js库到npm仓库
【JS】Chapter13-构造函数&数据常用函数
国产RK3399开发板如何在Ubuntu保留文件系统
微信小程序项目实例SSM项目校园活动报名网
Qt中的线程同步：确保多线程程序的安全性
使用 Clipdrop 替换长安三万里电影海报中的天空
【JS】js给对象动态添加、设置、删除属性名和属性值
一个用C#开发的操作系统的开源项目
P5718 【深基4.例2】找最小值
Python自动化测试面试题精选（一）

原文地址：https://blog.csdn.net/m0_45085885/article/details/126233017