【数学建模】线性规划

司守奎 《数学建模算法与应用》 第二版

线性规划问题是在一组线性约束条件的限制下，求一线性目标函数最大或最小的问题。

问题的约束条件记为s.t.(即subject to)。

由于上面的目标函数及约束条件均为线性函数，故称为线性规划问题。

matlab求解线性规划问题

matlab规定线性规划的标准形式

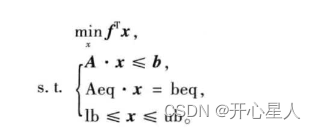
式中：f,x,b,beq,lb,ub为列向量，其中f称为价值向量，b称为资源向量；A,Aeq为矩阵。
Matlab中求解线性规划的命令为

[x,fval]linprog(f,A,b)
[x,fval]linprog(f,A,b,Aeq,beq)
[x,fval]linprog(f,A,b,Aeq,beq,lb,ub)
1
2
3

式中：x返回决策向量的取值；fval返回目标函数的最优值；f为价值向量；A和b对应线性不等式约束；Aeq和beq对应线性等式约束；lb和ub分别对应决策向量的下界向量和上界向量。

转换为标准形式

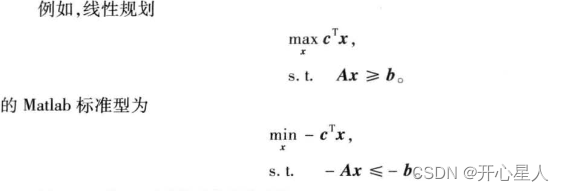
例题

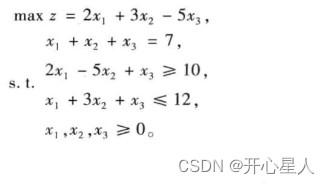
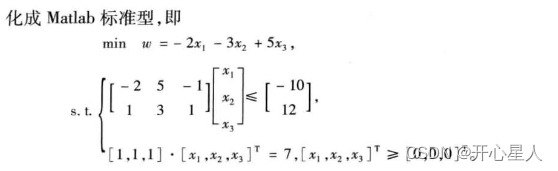
clc,clear;
f = [2; 3; -5];
a = [-2 5 -1; 1 3 1];
b = [-10; 12];
aeq = [1 1 1];
beq = 7;
lb = zeros(3, 1);
%//f取-f意为取反的最小值
[x, fval] = linprog(-f, a, b, aeq, beq, lb);
fprintf('x1=%.4f, x2=%.4f, x3=%.4f\nz=%.4f\n', x, -fval);
1
2
3
4
5
6
7
8
9
10

可以转换成线性规划的问题

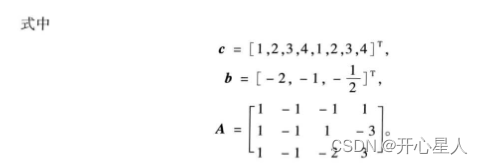
多目标规划问题

1）确定一个最大的风险率，所以可以将风险率放到约束条件中去了，而不是作为目标函数

2）确定一个最小的收益，所以可以将收益放到约束条件中去了，而不是作为目标函数

3)对不同的目标附上权重