LeetCode952三部曲之一：解题思路和初级解法(137ms，超39%)

欢迎访问我的GitHub

这里分类和汇总了欣宸的全部原创(含配套源码)：https://github.com/zq2599/blog_demos

题目描述

• 难度：困难
• 编程语言：Java
• 给定一个由不同正整数的组成的非空数组 nums ，考虑下面的图：

1. 有 nums.length 个节点，按从 nums[0] 到 nums[nums.length - 1] 标记；
2. 只有当 nums[i] 和 nums[j] 共用一个大于 1 的公因数时，nums[i] 和 nums[j]之间才有一条边。

• 返回图中最大连通组件的大小
• 示例 1：
  

输入：nums = [4,6,15,35]
输出：4
1
2

• 示例 2：
  

输入：nums = [20,50,9,63]
输出：2
1
2

• 示例 3：
  

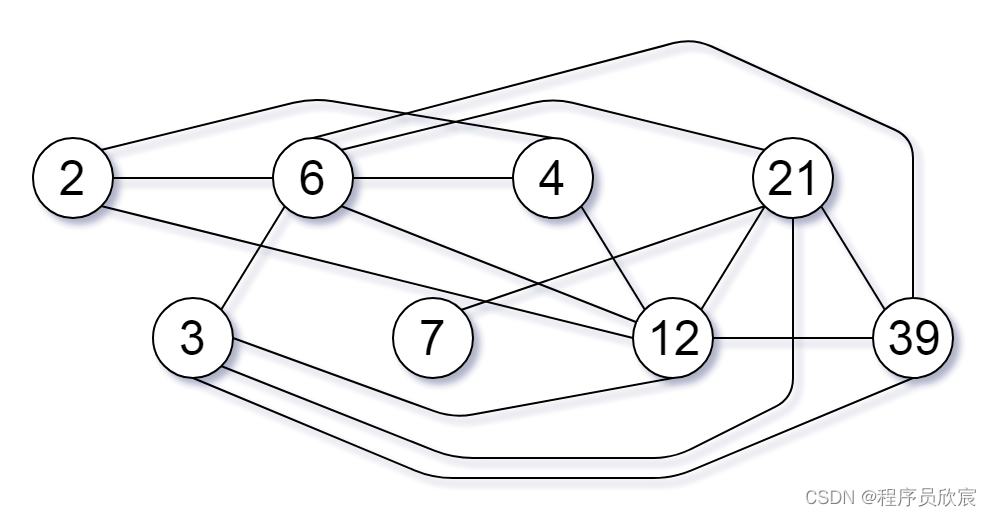
输入：nums = [2,3,6,7,4,12,21,39]
输出：8
1
2

• 提示：
• 1 <= nums.length <= 2 * 104
• 1 <= nums[i] <= 105
• nums 中所有值都 不同

审题

• 可能是自身天资愚钝，欣宸第一时间居然没有搞懂题目中连通组件的大小的含义，以示例一为例，如下图，明明是三个边，为啥答案是4？
  
• 好吧，晕晕乎乎的想了半天终于搞清楚了：

1. 不是让你数有几条边！
2. 是让你数能够连在一起的元素，最多有几个？
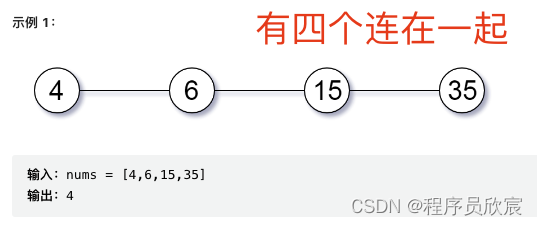
3. 如下图，有四个连在一起，答案就是4
   
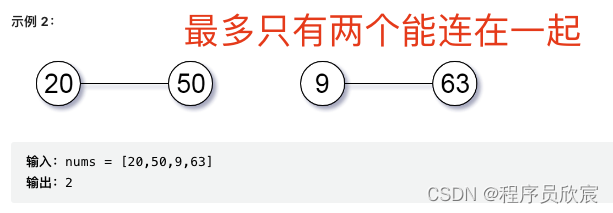
4. 如下图，50和9之间没有公因数，所以连不起来，导致四个数字中，20和50相连，9和63相连，那么，能连在一起的两个组合中，每个组合的数量都是2，答案就是2
   

• 磕磕绊绊终于读懂了题，再来看看解题前对知识储备的要求

需要哪些基本功？

• 请先掌握下面两个基本功，然后再能愉快的解题和优化，享受AC的喜悦，以及超过人数百分比提升的成就感
• 计算素数（埃氏筛选或者欧拉筛选，我这里用的是欧拉筛选）
• 并查集，需掌握以下技术点：

1. 数据结构是数组，下标代表数字，值代表父节点是谁
2. 查找（查找时顺便优化路径）
3. 合并

• 上述基本功相信难不倒聪明的您，半小时内就能掌握，接下来，在欣宸图文并茂的解说中，一起享受解hard题的快乐吧

题目中还有哪些重要信息？

• 除了基本命题，还有三个至关重要的信息需要重点关注，他们是解题的关键，如下图，请记住这三个信息，很快就会用到
  
• 至此，准备工作已经完成，可以开始分析解题思路了，图文并茂的分析中，可能会让您产生一个错觉：hard题，就这？

解题思路

• 先画个图来描述完整流程
  
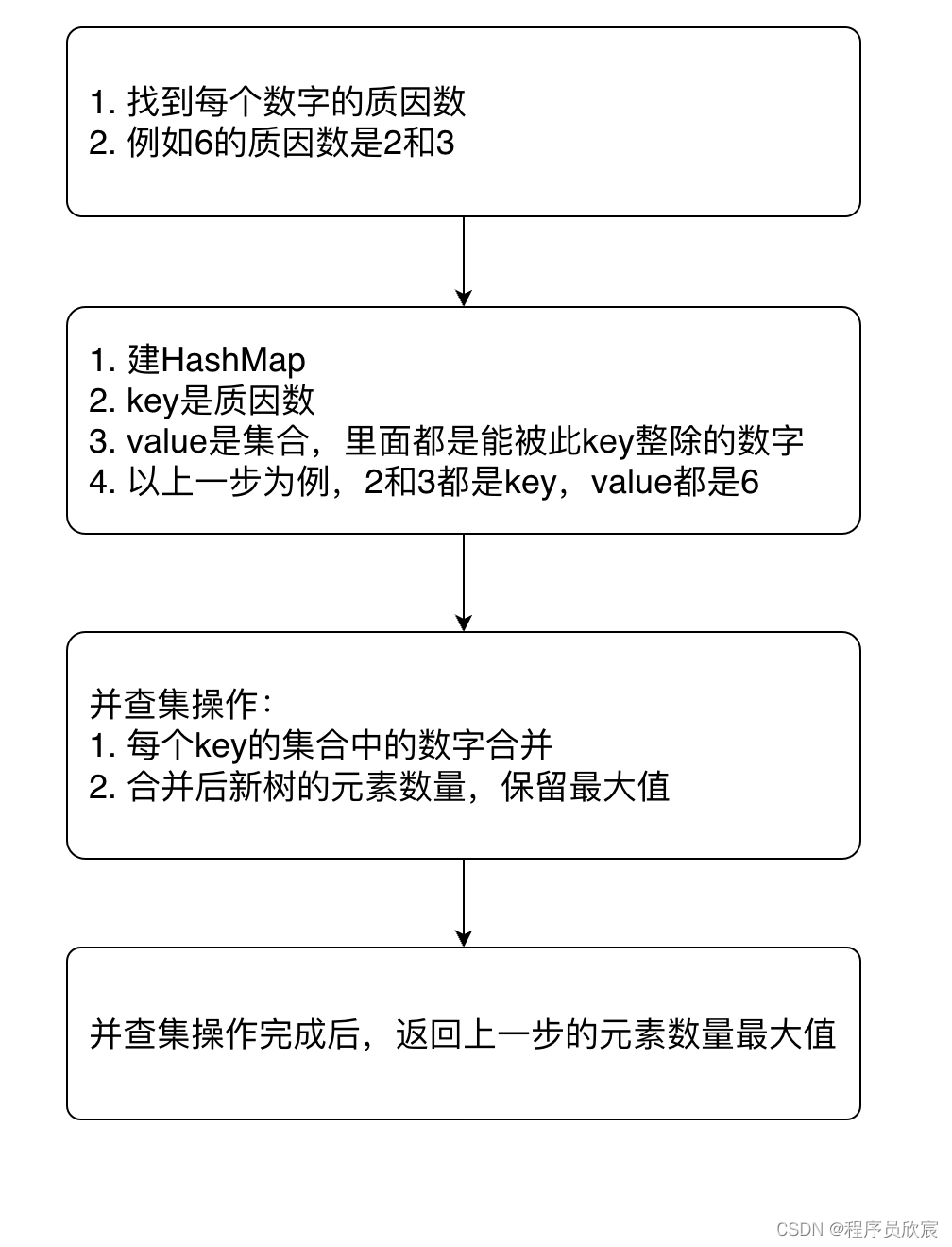
• 上面这个图，一开始可能您会看得有点晕乎，HashMap到底存了啥？并查集合并又合并了啥？
• 看不明白没事，真的没事，此图其实是解题思路的提前小结，接下来咱们用实际数字来演示解题思路，总之，就是要以最简单和具体的手段让您理解思路

实例解题演示解题思路

• 注意，接下来还是分析思路，暂时不涉及代码
• 以官方的示例来演示解题过程吧，假设输入数组有四个数字：4、6、15、35
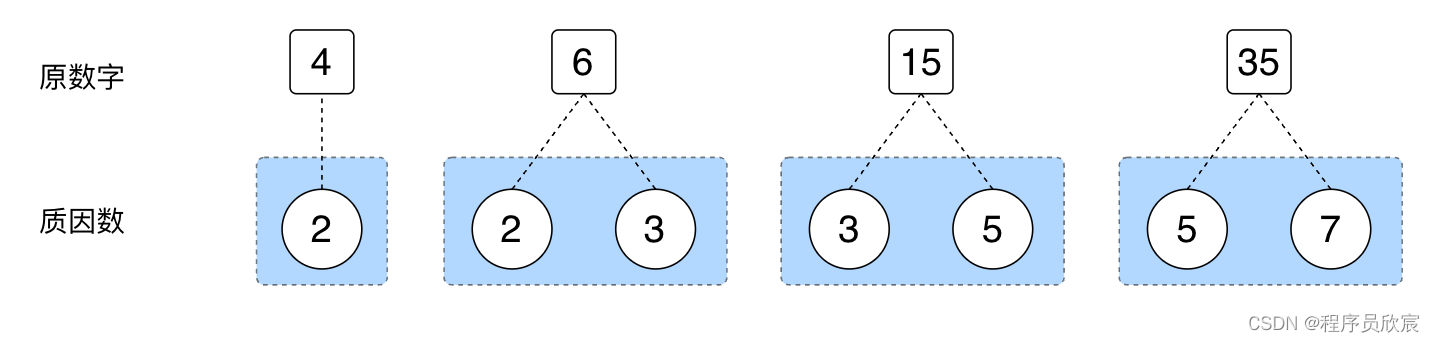
• 首先，计算出每个数字的质因数，如下图，4的质因数是2，6的质因数是2和3，应该很好理解
  
• 接下来，根据上面的计算结果，新建一个HashMap，key是质因数，value是原数字，以2为例，它是4和6的质因数，所以，key就是2，value是个ArrayList，里面的内容是4和6，也就是说，根据上面的图得出下面的图
  
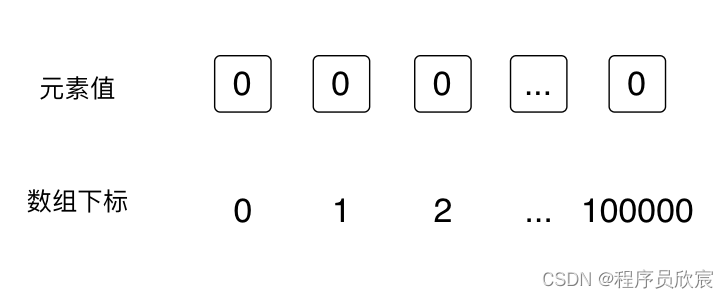
• 现在新建一个并查集，由于数字大小范围是从1到100000，所以，为了用数组下标表示数字，组数的大小就是100001，如此一来，array[100000]=123的意思就是：100000这个数字的父节点是123，这就是并查集概念中的数组定义的标准含义了
• 注意，数组创建后，每个元素值都是0，如下图
  
• 在本题中，咱们只关心4、6、15、35这四个数字，所以接下来画图的时候，数组中其他数字就不画上去了，后面的分析中，数组画出来就是下图的效果，相信您可以理解
  
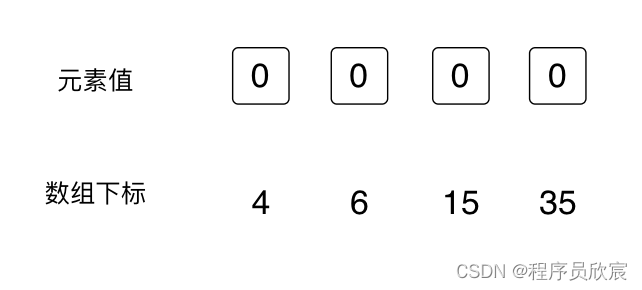
• 按照并查集的定义，最初的时候，每个元素的父节点是它自己，所以给数组中每个元素赋值，值就等于数组下标，如下图所示，注意下图新增了辅助理解的逻辑图，这个是用来帮助大家理解每个节点和父节点关系的，可以看到每个节点的箭头指向自己，表示自己是自己的父节点（或者说每个元素都是根节点）
  
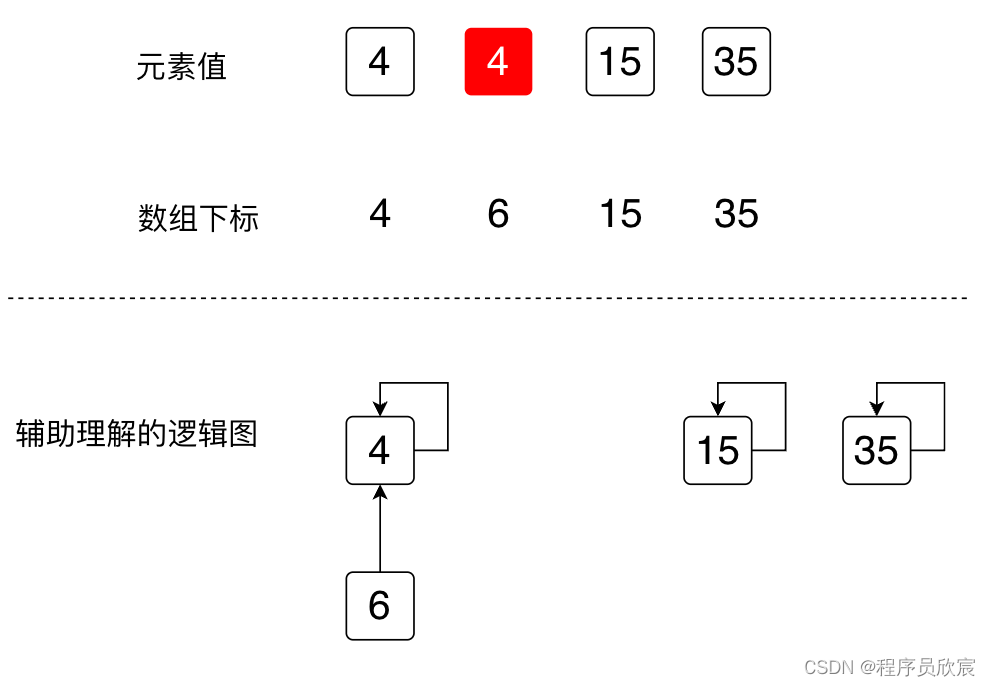
• 接下来，遍历前面准备好的HashMap，每个key对应的都是一个List，将这个list中的所有元素在并查集中合并，以key等于2为例，value中有两个数字：4和6，所以，在并查集中将4和6合并
• 第一个key是2，value中的数字是4和6，将4和6合并的效果如下图，红色是改过的地方，值等于4，表示数字6的父节点改成了4，为了便于理解，逻辑图也同步改动了，6指向自己的父节点4
  
• 第二个key是3，value中的数字是6和15，将6和15合并的效果如下图，蓝色是改过的地方，值等于6，表示数字15的父节点改成了6，为了便于理解，逻辑图也同步改动了，15指向自己的父节点6（逻辑图上可见，尽管只改了15的父节点，然而4，6，15已经在同一个树下了）
  
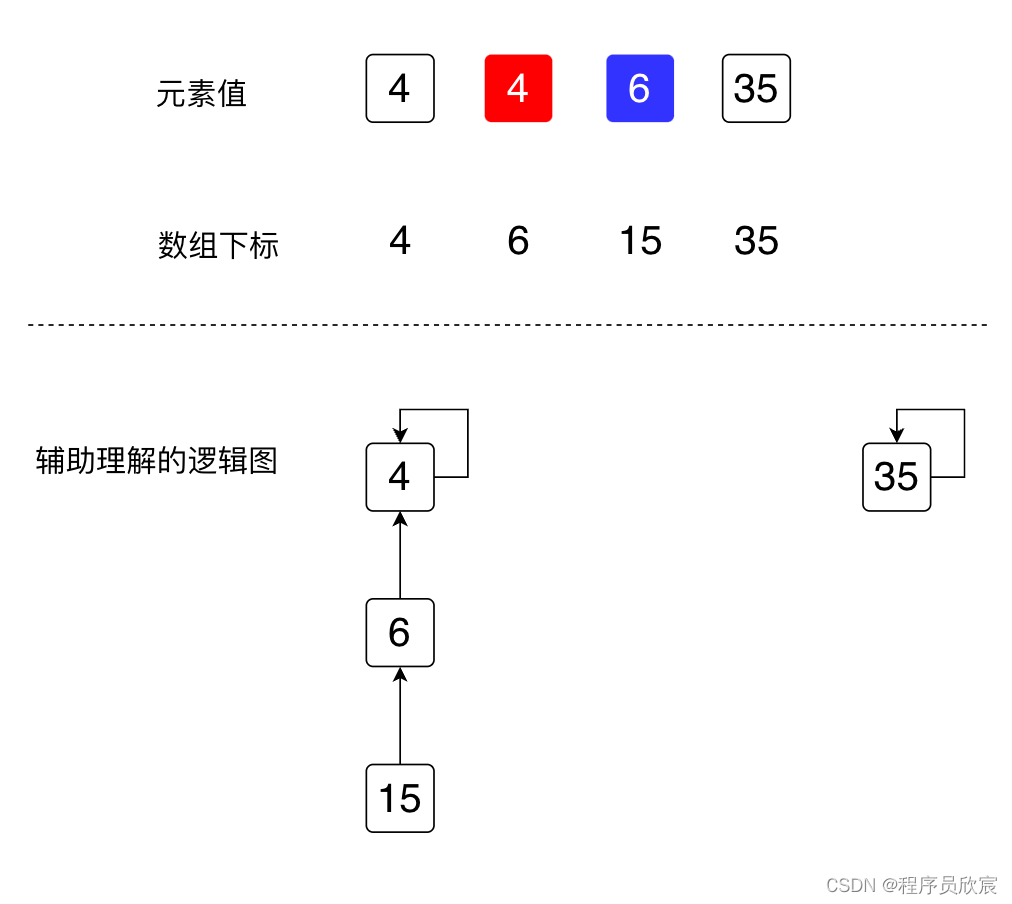
• 第三个key是5，value中的数字是15和35，将15和15合并的效果如下图，绿色是改过的地方，值等于15，表示数字35的父节点改成了15，为了便于理解，逻辑图也同步改动了，35指向自己的父节点15
  
• 至于第四个key，即7，它的value中只有一个数字35，谈不上合并，所以不做任何操作
• 至此，并查集合并操作完成，纵观整个并查树，虽然有多个树，唯有以4为根节点的树，其元素最多，有四个，所以，此题返回值就是4，连通的四个元素是4-6-15-35
• 画图画到手抽筋，相信您对解题思路已经完全掌握，接下来，开始编码吧

编码

• 接下来的编码，先将几个关键点逐个列举，然后再给出完整代码，并且会附上详细的注解，相信您可以轻松读懂
• 首先看看要定义哪些成员变量，如下，map是最重要的，刚才咱们详细分析过，代码注解也说得很细致了，然后是fathers、rootSetSize、maxRootSetSize都是并查集相关的数据结构

	// 并查集的数组， fathers[3]=1的意思是：数字3的父节点是1
    int[] fathers = new int[100001];

    // 并查集中，每个数字与其子节点的元素数量总和，rootSetSize[5]=10的意思是：数字5与其所有子节点加在一起，一共有10个元素
    int[] rootSetSize = new int[100001];

    // map的key是质因数，value是以此key作为质因数的数字
    // 例如题目的数组是[4,6,15,35]，对应的map就有四个key：2,3,5,7
    // key等于2时，value是[4,6]，因为4和6的质因数都有2
    // key等于3时，value是[6,15]，因为6和16的质因数都有3
    // key等于5时，value是[15,35]，因为15和35的质因数都有5
    // key等于7时，value是[35]，因为35的质因数有7
    Map<Integer, List<Integer>> map = new HashMap<>();

    // 用来保存并查集中，最大树的元素数量
    int maxRootSetSize = 1;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

• 并查集的查找根节点的操作也要注意，在查找过程中，将每个元素的父节点都改成了根节点，这就是常规的压缩操作

    /**
     * 带压缩的并查集查找(即寻找指定数字的根节点)
     * @param i
     */
    private int find(int i) {
        // 如果执向的是自己，那就是根节点了
        if(fathers[i]==i) {
            return i;
        }

        // 用递归的方式寻找，并且将整个路径上所有长辈节点的父节点都改成根节点，
        // 例如1的父节点是2，2的父节点是3，3的父节点是4，4就是根节点，在这次查找后，1的父节点变成了4，2的父节点也变成了4，3的父节点还是4
        fathers[i] = find(fathers[i]);
        return fathers[i];
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

• 并查集的合并操作也有个细节要注意，每次合并后，根节点下属元素会增加，将总数统一出来，再和maxRootSetSize比较一下，这样持续的操作后，maxRootSetSize记录的就是最大的树的元素个数

    /**
     * 并查集合并，合并后，child会成为parent的子节点
     * @param parent
     * @param child
     */
    private void union(int parent, int child) {
        int parentRoot = find(parent);
        int childRoot = find(child);

        // 如果有共同根节点，就提前返回
        if (parentRoot==childRoot) {
            return;
        }

        // child元素根节点是childRoot，现在将childRoot的父节点从它自己改成了parentRoot，
        // 这就相当于child所在的整棵树都拿给parent的根节点做子树了
        fathers[childRoot] = fathers[parentRoot];

        // 合并后，这个树变大了，新增元素的数量等于被合并的字数元素数量
        rootSetSize[parentRoot] += rootSetSize[childRoot];

        // 更像最大数量
        maxRootSetSize = Math.max(maxRootSetSize, rootSetSize[parentRoot]);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

• 在来看一下得到数字的质因数的操作，如下所示：

        // 对数组中的每个数，算出所有质因数，构建map
        for (int i=0;i<nums.length;i++) {
            int cur = nums[i];

            for (int j=2;j*j<=cur;j++) {
                // 从2开始逐个增加，能整除的一定是质数
                if(cur%j==0) {
                    map.computeIfAbsent(j, key -> new ArrayList<>()).add(nums[i]);
                }

                // 从cur中将j的因数全部去掉
                while (cur%j==0) {
                    cur /= j;
                }
            }

            // 能走到这里，cur一定是个质数，
            // 因为nums[i]被除过多次后结果是cur，所以nums[i]能被cur整除，所以cur是nums[i]的质因数，应该放入map中
            if (cur!=1) {
                map.computeIfAbsent(cur, key -> new ArrayList<>()).add(nums[i]);
            }
        }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

• 关键代码已经看完了，来看看完整版代码

class Solution {
    
    // 并查集的数组， fathers[3]=1的意思是：数字3的父节点是1
    int[] fathers = new int[100001];

    // 并查集中，每个数字与其子节点的元素数量总和，rootSetSize[5]=10的意思是：数字5与其所有子节点加在一起，一共有10个元素
    int[] rootSetSize = new int[100001];

    // map的key是质因数，value是以此key作为质因数的数字
    // 例如题目的数组是[4,6,15,35]，对应的map就有四个key：2,3,5,7
    // key等于2时，value是[4,6]，因为4和6的质因数都有2
    // key等于3时，value是[6,15]，因为6和16的质因数都有3
    // key等于5时，value是[15,35]，因为15和35的质因数都有5
    // key等于7时，value是[35]，因为35的质因数有7
    Map<Integer, List<Integer>> map = new HashMap<>();

    // 用来保存并查集中，最大树的元素数量
    int maxRootSetSize = 1;

    /**
     * 带压缩的并查集查找(即寻找指定数字的根节点)
     * @param i
     */
    private int find(int i) {
        // 如果执向的是自己，那就是根节点了
        if(fathers[i]==i) {
            return i;
        }

        // 用递归的方式寻找，并且将整个路径上所有长辈节点的父节点都改成根节点，
        // 例如1的父节点是2，2的父节点是3，3的父节点是4，4就是根节点，在这次查找后，1的父节点变成了4，2的父节点也变成了4，3的父节点还是4
        fathers[i] = find(fathers[i]);
        return fathers[i];
    }

    /**
     * 并查集合并，合并后，child会成为parent的子节点
     * @param parent
     * @param child
     */
    private void union(int parent, int child) {
        int parentRoot = find(parent);
        int childRoot = find(child);

        // 如果有共同根节点，就提前返回
        if (parentRoot==childRoot) {
            return;
        }

        // child元素根节点是childRoot，现在将childRoot的父节点从它自己改成了parentRoot，
        // 这就相当于child所在的整棵树都拿给parent的根节点做子树了
        fathers[childRoot] = fathers[parentRoot];

        // 合并后，这个树变大了，新增元素的数量等于被合并的字数元素数量
        rootSetSize[parentRoot] += rootSetSize[childRoot];

        // 更像最大数量
        maxRootSetSize = Math.max(maxRootSetSize, rootSetSize[parentRoot]);
    }

    public int largestComponentSize(int[] nums) {

        // 对数组中的每个数，算出所有质因数，构建map
        for (int i=0;i<nums.length;i++) {
            int cur = nums[i];

            for (int j=2;j*j<=cur;j++) {
                // 从2开始逐个增加，能整除的一定是质数
                if(cur%j==0) {
                    map.computeIfAbsent(j, key -> new ArrayList<>()).add(nums[i]);
                }

                // 从cur中将j的因数全部去掉
                while (cur%j==0) {
                    cur /= j;
                }
            }

            // 能走到这里，cur一定是个质数，
            // 因为nums[i]被除过多次后结果是cur，所以nums[i]能被cur整除，所以cur是nums[i]的质因数，应该放入map中
            if (cur!=1) {
                map.computeIfAbsent(cur, key -> new ArrayList<>()).add(nums[i]);
            }
        }

        // 至此，map已经准备好了，接下来是并查集的事情，先要初始化数组
        for(int i=0;i< fathers.length;i++) {
            // 这就表示：数字i的父节点是自己
            fathers[i] = i;
            // 这就表示：数字i加上其下所有子节点的数量等于1（因为每个节点父节点都是自己，所以每个节点都没有子节点）
            rootSetSize[i] = 1;
        }

        // 遍历map
        for (int key : map.keySet()) {
            // 每个key都是一个质因数
            // 每个value都是这个质因数对应的数字
            List<Integer> list = map.get(key);

            // 超过1个元素才有必要合并
            if (null!=list && list.size()>1) {
                // 取第0个元素作为父节点
                int parent = list.get(0);

                // 将其他节点全部作为地0个元素的子节点
                for(int i=1;i<list.size();i++) {
                    union(parent, list.get(i));
                }
            }
        }

        return maxRootSetSize;
    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115

• 在LeetCode上提交，结果如下图，137ms，超过39.55%的用户
  
• 至此，初步尝试已经通过，尽管耗时偏高，39%的比例也过于勉强，但证明本题的解题思路是走得通的
• 本文接下来的篇幅，是对自己在解题过程中犯错的复盘，放在这里供您参考，如果您也有类似困惑，希望接下来的内容可以帮助到您

何为连通？

• 通过因数2可将 4, 6, 12连通，这句话啥意思？在看LeetCode高手们的解题过程时，常常看到他们提到连通，最初我是很难理解这个概念
• 这句话的意思是，因为4，6，12有共同的因数2，所以，4和6可以连线，4和12也可以连线，6和12也可以连线，简单的说就是有共同因素的数字，它们是可以随意连接的！

最大的误解

• 个人在做这道题的时候，最大的误解就是对并查集合并的理解错误，导致做错，这里列出来，以避免您犯相同错误

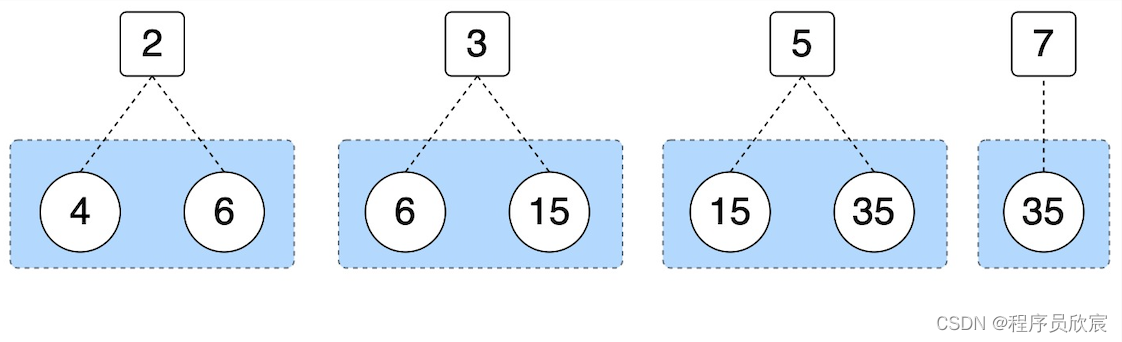
• 以4,6,15,35这四个数字为例，以2为质因数的有4和6，以3为质因数的有6和15，以5为质因数的有15和35，以7为质因数的有35，逻辑关系如下图
  

• 所以，我们在说并查集合并操作，到底在合并什么？（这是核心，理解正确，这道题就解开了）

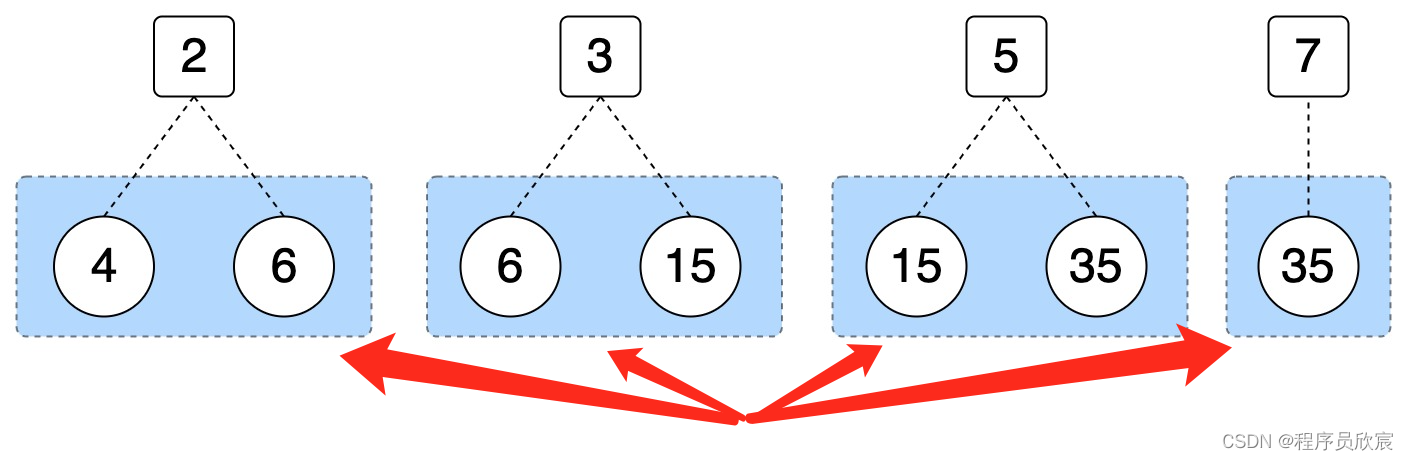
• 之前的误解如下图，以为是将红色箭头指向的四个集合合并，这样就达到了连通效果，实际上这样的理解是大错特错
  

• 接下来是自我救赎的纠正之路

• 首先，图就是错误的，既然是并查集，就应该按照并查集的数据结构来画图：一个int数组，数组下标就代表具体数字，值代表该数字的父节点是谁，例如 a[2]=5，其含义就是数字2的父节点是5，这是基本定义

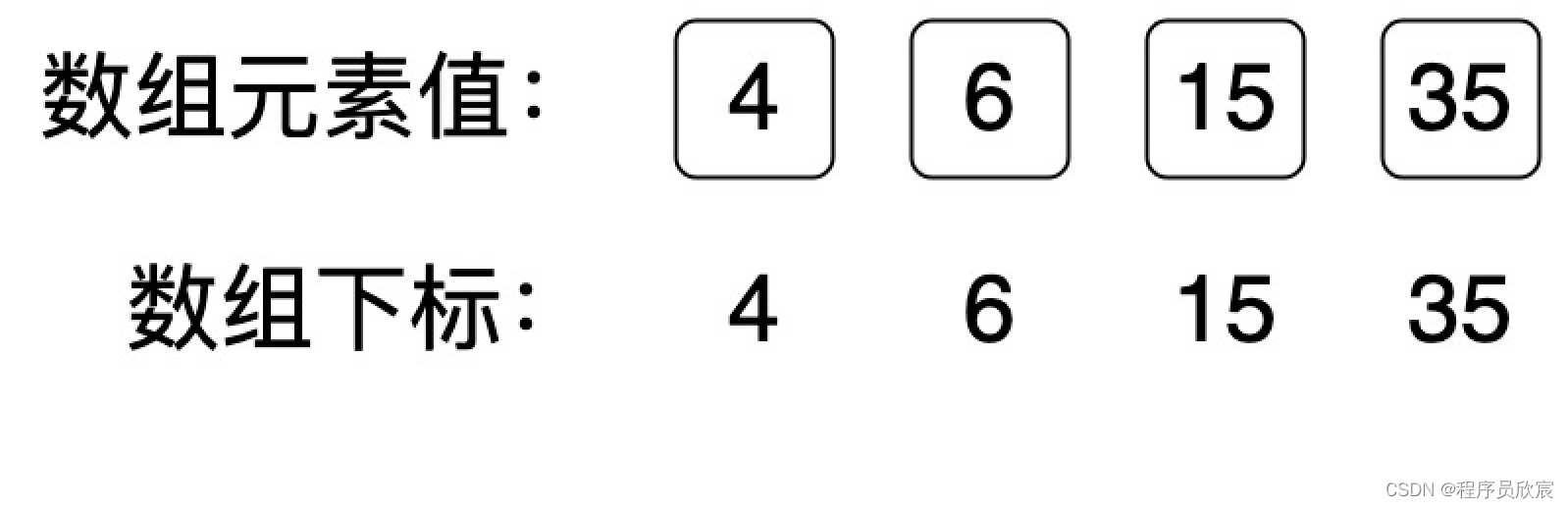
• 并查集初始化的时候，每个元素的父节点都是它自己，如下图，注意，这个数组的长度其实是36（既从0到35），但是其他元素都用不上，所以我们无需关注它们，也就没有画进图中
  

• 接下来就是本题最核心的操作：合并，究竟该怎么合并呢？

• 答案是：相同质因数的数字合并，也就是说：以2为质因数的是4和6，所以4和6合并，以3为质因数的是6和15，所以6和15合并，以5为质因数的是15和35，所以15和35合并，7的质因数只有35，那就没法合并了

• 以上就是合并的操作，没错，就是这么简单：在并查集中对拥有相同质因数的数字进行合并

• 看到这里，您应该会疑惑：这样的合并，和连通有什么关系？和解题又有什么关系呢？

• 不急，咱能就用上面的数组，合并一下试试，稍后就会见证奇迹，也许能帮您找到豁然开朗的感觉

• 为了形象的理解，接下来我给数组再配上图，用来更形象的表达元素之间的父子关系，合并前的数组和关系图如下图，每个圆圈都有个箭头指向自己，表示每个元素的父节点是自己
  

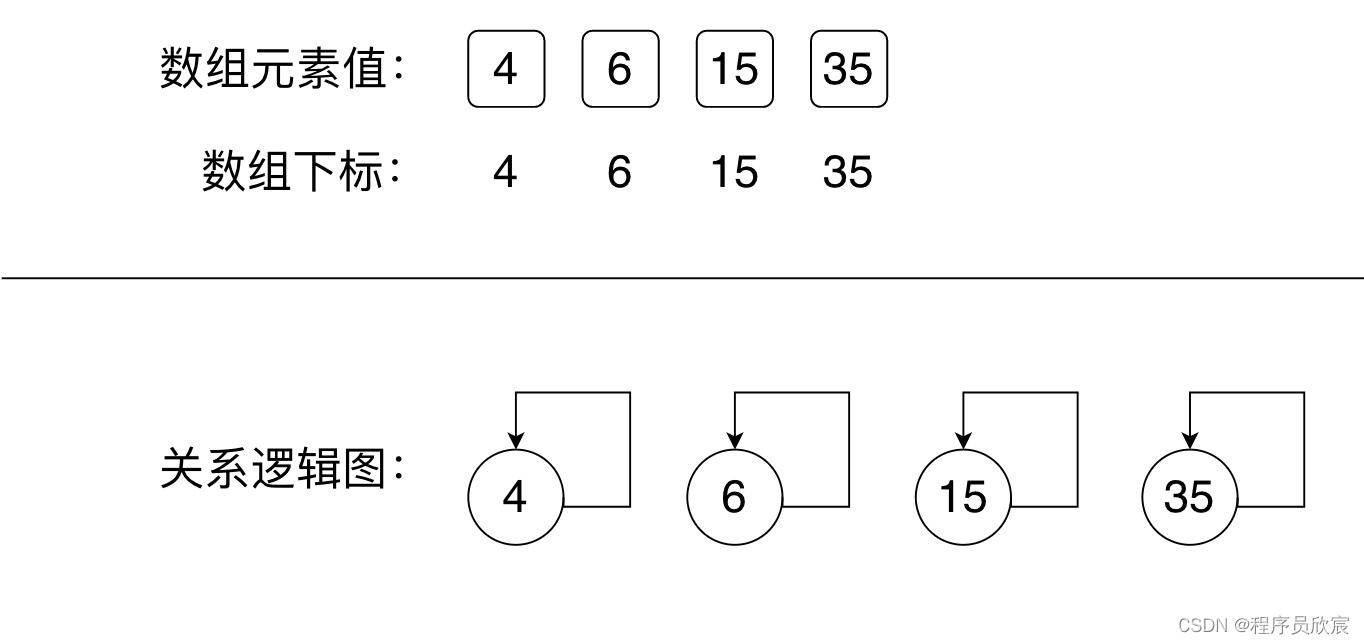
• 接下来，合并4和6，这里的做法是把4作为6的父节点，所以，如下图，数组下标为4的元素值等于6，用逻辑图来表示，就是6的箭头指向4
  

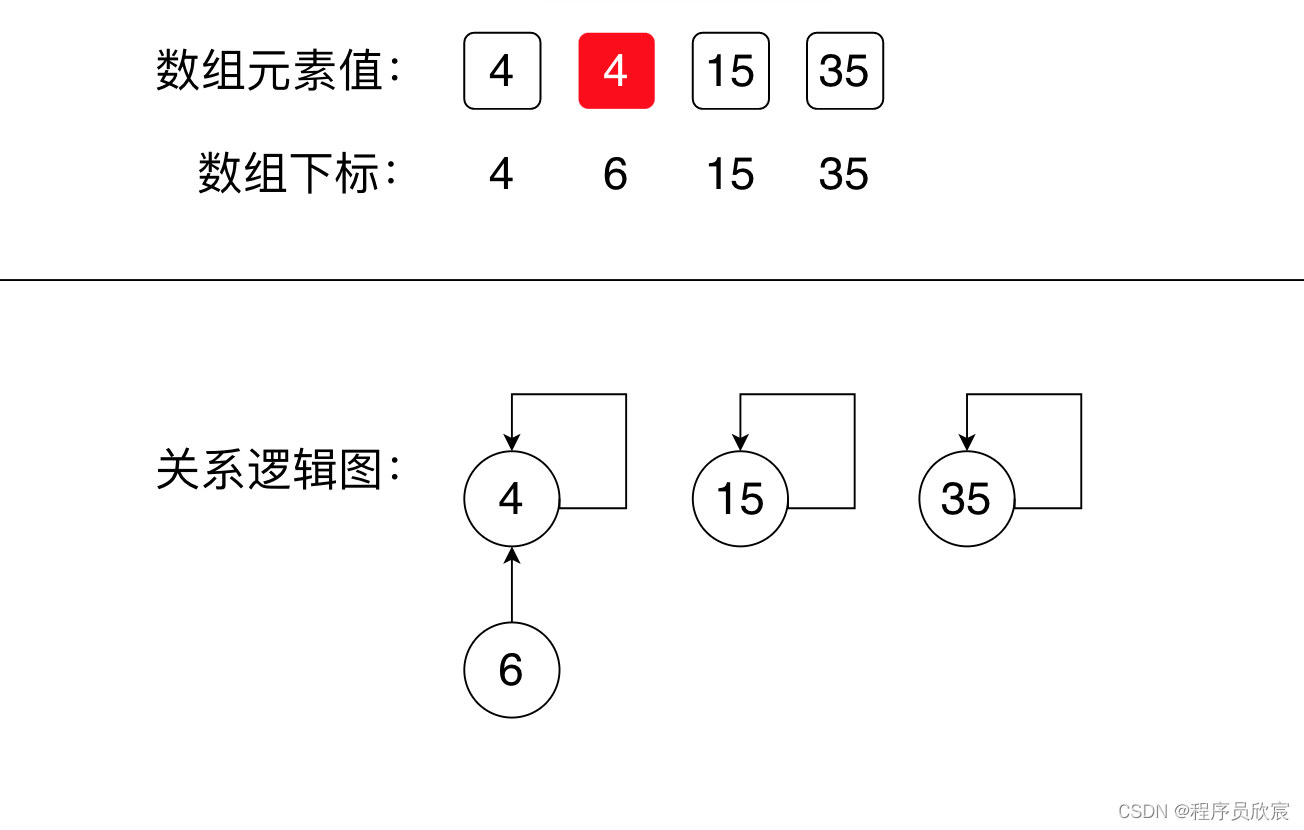
• 接下来该合并6和15了，它们都有质因数3，这一步非常关键，因为我就是在这一步恍然大悟的，如下图，将6的父节点设置为4，再看逻辑关系图，明明只是在合并6和15，然而，4、6、15已经连通了！
  

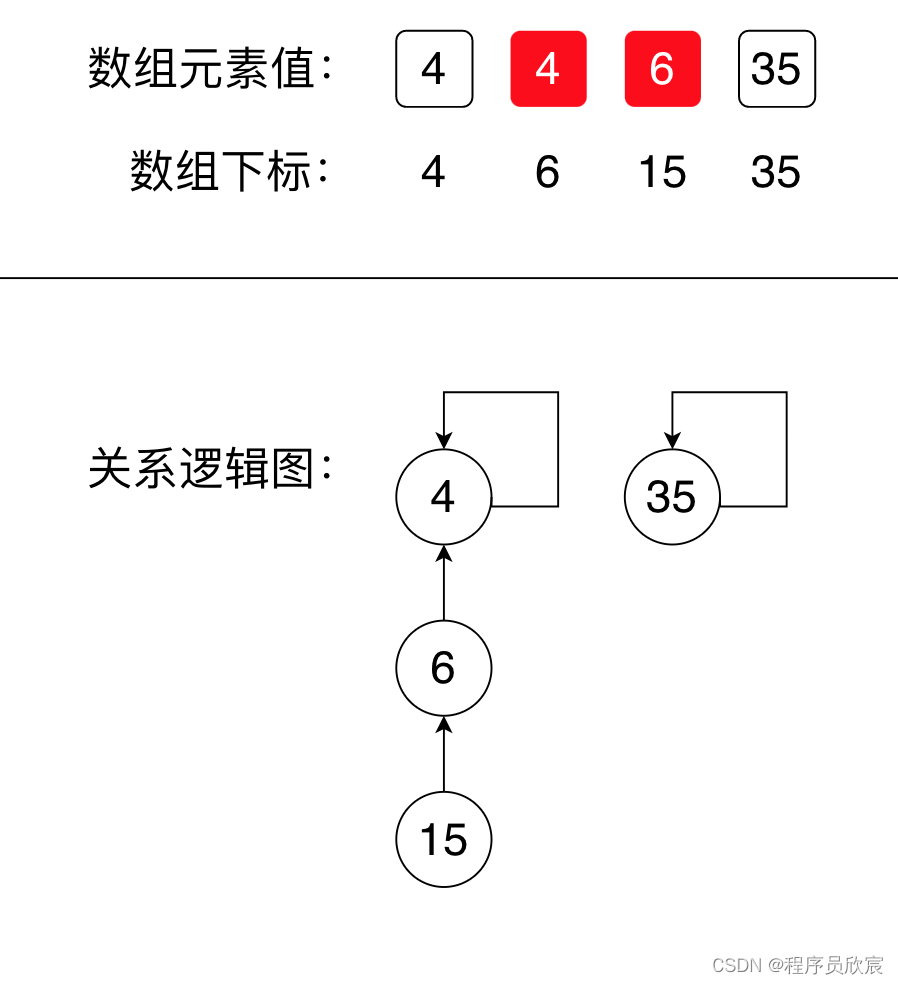
• 恍然大悟：我们无需对各个质因数之间做什么，只要将每个质因数对应的数字合并即可，有的数字本来就属于多个质因数，所有跨质因数的连接都是因为这个特点而存在！

• 接下来是连接15和35，相信聪明的您也已经彻底领悟了，此时4个元素已经连通了
  

• 最后质因数7对应的数字只有35，一个数字就不需要合并操作了

敬请期待

• 至此，952的解题思路以及最初级的解法实战已经完成，这么多图和示例，相信聪明的您对解答此题已经胸有成竹，然而耗时过长，超39%实在是过于落后了，不能忍，所以，接下来的章节咱们一起来对此题做第一次优化，看看能不能有所提升

你不孤单，欣宸原创一路相伴

1. Java系列
2. Spring系列
3. Docker系列
4. kubernetes系列
5. 数据库+中间件系列
6. DevOps系列