图像金字塔

图像金字塔介绍

图像金字塔是图像中多尺度表达的一种，最主要用于图像的分割，是一种以多分辨率来解释图像的有效且概念简单的结构。简单来说，图像金字塔是同一图像不同分辨率的子图集合（有800×800、480×640…）

图像金字塔最初用于机器视觉和图像压缩，一幅图像的金字塔是一系列以金字塔形状排列的分辨率逐渐降低、且来源于同一张原始图的图像集合。其通过梯次向下采样获得，直到达到某个终止条件才停止采样。

金字塔的底部是待处理图像的高分辨率表示，而顶部是低分辨率的近似。我们将一层一层的图像比喻成金字塔，层级越高，则图像越小，分辨率越低

高斯金字塔固定了缩放比，即如果你是800×800的图，无法缩放成500×500

我们将要学习用什么方法，如何去生成这些图像金字塔

---

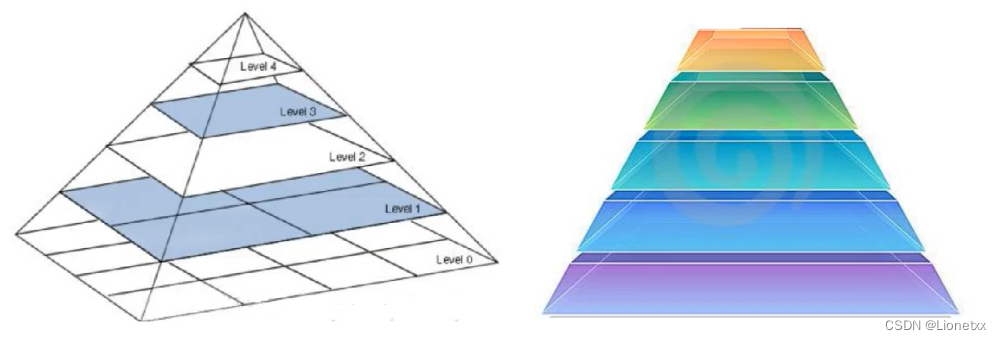
常见两类图像金字塔：

• 高斯金字塔（Gaussian pyramid）：用来向下/降采样（分辨率减小，图片变小，向上走），是主要的图像金字塔；
• 拉普拉斯金字塔（Laplacian pyramid）：用来从金字塔低层图像重建上层未采样图像，在数字图像处理中也就是预测残差，可以对图像进行最大程度的还原，配合高斯金字塔一起使用

高斯金字塔（Gaussian pyramid）

高斯金字塔是通过高斯平滑和亚采样（一个图形中取出一小块）获得的一系列下采样图像

向下采样

原理非常简单：如下图所示

原始图像分辨率M*N ——> 处理图像后分辨率M/2 * N/2；即每次处理后，结果是原来的1/4（不要求是偶数，会自动四舍五入）

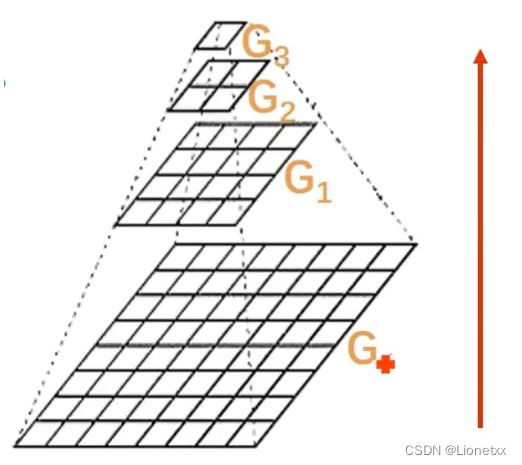
注意：向下采样（分辨率减小，在上图中表现为方向向上）会丢失信息

关键API：cv2.pyrDown(src[, dst[, dstsize[, borderType]]])
其中：

• src：需要操作的图片
• dst：返回值，不用写，我们用一个参数接受即可
• dstsize：返回图片的大小
• 图片会变成原来的1/4

# 高斯金字塔 ——> 向下采样

import cv2
import numpy as np

img = cv2.imread('./lena.png')

# 分辨率减小的操作：下采样
dst = cv2.pyrDown(img)

# 还可再变化多次
dst2 = cv2.pyrDown(dst)

# 展示
cv2.imshow('img',img)
cv2.imshow('dst',dst)
cv2.imshow('dst2',dst2)

cv2.waitKey(0)
cv2.destroyAllWindows()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

结果：

其实清晰度几乎没变，这就是图像金字塔的厉害之处：虽然丢掉了偶数行和偶数列，但是经过了高斯核函数卷积后，相当于把一个像素点匀到周围了，因此变化不大

---

向上采样

向上采样是向下采样的相反过程，指图片从小变大的过程

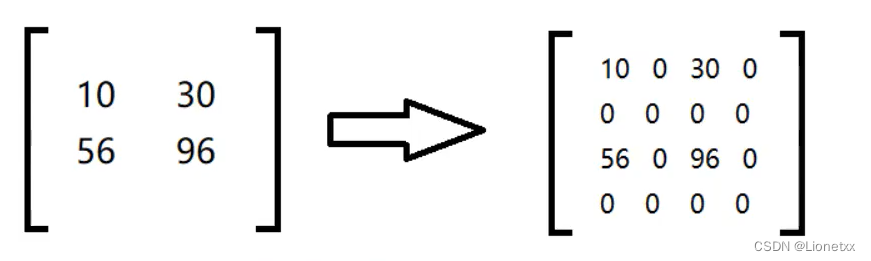
1. 将图像在每个方向扩大为原来的两倍，新增的行和列以0填充
2. 使用先前同样的内核（乘以4）于放大后的图像卷积，获取近似值 ——> 假设四个一组，相当于把有数值的地方向周围三个0的位置填充**（以左上角为例，相当于把10分成四份，一份2.5；但是由于整体值变小了，图像会偏暗，为了解决这个问题，我们乘4，相当于“复制”四份）**

操作和向下采样一样！

关键API：cv2.pyrUp(src[, dst[, dstsize[, borderType]]])
其中：

• src：需要操作的图片
• dst：返回值，不用写，我们用一个参数接受即可
• dstsize：返回图片的大小
• 图片会变成原来的4倍

# 高斯金字塔 ——> 向上采样

import cv2
import numpy as np

img = cv2.imread('./Hello.jpeg')

# 分辨率减小的操作：下采样
dst = cv2.pyrUp(img)

# 还可再变化多次
# dst2 = cv2.pyrUp(dst)

# 展示
cv2.imshow('img',img)
cv2.imshow('dst',dst)
# cv2.imshow('dst2',dst2)

cv2.waitKey(0)
cv2.destroyAllWindows()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

结果：

---

拉普拉斯金字塔

拉普拉斯金字塔图像 = 原始图像 - 上采操作函数（下采操作函数(原始图像)）
1

将降采样之后的图像在进行上采样操作，然后与之前还没降采样的原图进行做差得到残差图！为还原图像做信息的准备！

也就是说，拉普拉斯金字塔是通用原图像减去先缩小后再放大的图像（高斯金字塔） 的一系列图像构成的，减去后得到的结果就是拉普拉斯金字塔的图像。保留的是残差！

拉普拉斯金字塔是由高斯金字塔构成的，没有专门的函数

# 拉普拉斯金字塔
# 原图 - 先缩小再放大的图（这样才能变回原图大小，方便做差）

import cv2
import numpy as np

img = cv2.imread('./lena.png')

# 先缩小
temp = cv2.pyrDown(img)

# 再放大
dst = cv2.pyrUp(temp)

# 原图 和 高斯金字塔 的差就是 拉普拉斯金字塔
lap0 = img - dst

# 展示
# cv2.imshow('img',img)
cv2.imshow('dst',dst)
cv2.imshow('lap0',lap0)

cv2.waitKey(0)
cv2.destroyAllWindows()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

结果：

---

图像直方图

图像直方图的基本概念

在统计学中，直方图是一种对数据分布情况的图形表示，是一种二维统计图表

图像直方图是用于表示数字图像中亮度分布的直方图，标绘了图像中每个亮度值的像素数。

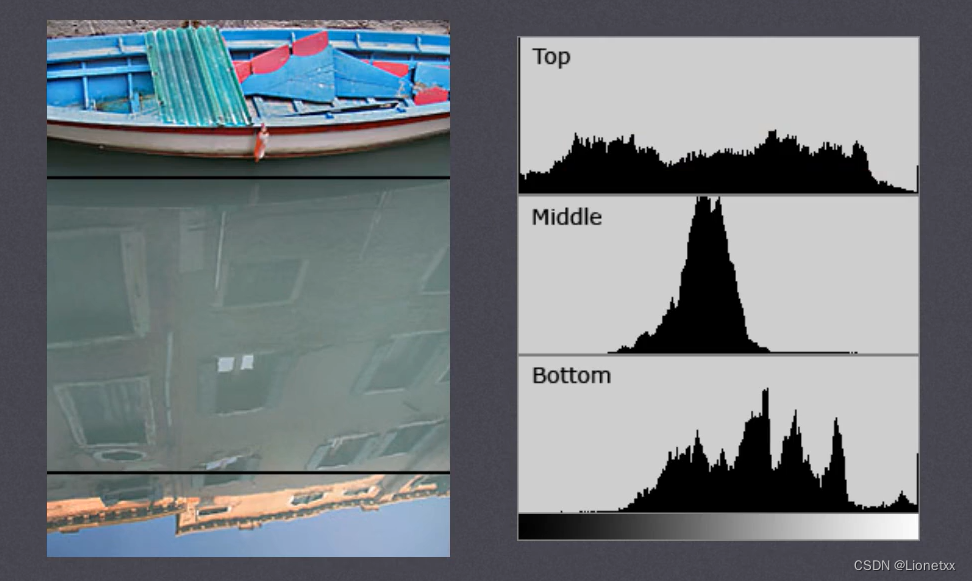
可以借助观察该直方图了解需要如何调整亮度分布的直方图。这种直方图中，横坐标的左侧为纯黑、较暗的区域，而右侧为较亮、纯白的区域。

因此，一张较暗图片的图像直方图的数据多集中于左侧和中间部分，而整体明亮，只有少量阴影的图像则相反

• 横坐标：图像中各个像素点的灰度级（灰度值0-255每一个数字都是一个灰度级）
• 纵坐标：具有该灰度级的像素个数

我们从图像直方图可以看出：该幅图像存在较多很暗或者很亮的点（具有这些灰度级的像素个数较多），反而亮暗平衡的点较少**（具有这些灰度级的像素个数较少）**

看懂了之后我们就可以自主分析下面三张图啦（懒得写了…）

---

举个🌰：
有个3×3的图片，其中

• 像素的灰度级表示 ——> 图片中有什么数字
• 具有该灰度级的像素个数表示 ——> 这个数字在图片中出现了几次

画出上图的直方图，直方图可以有很多种。比如：
折线图：

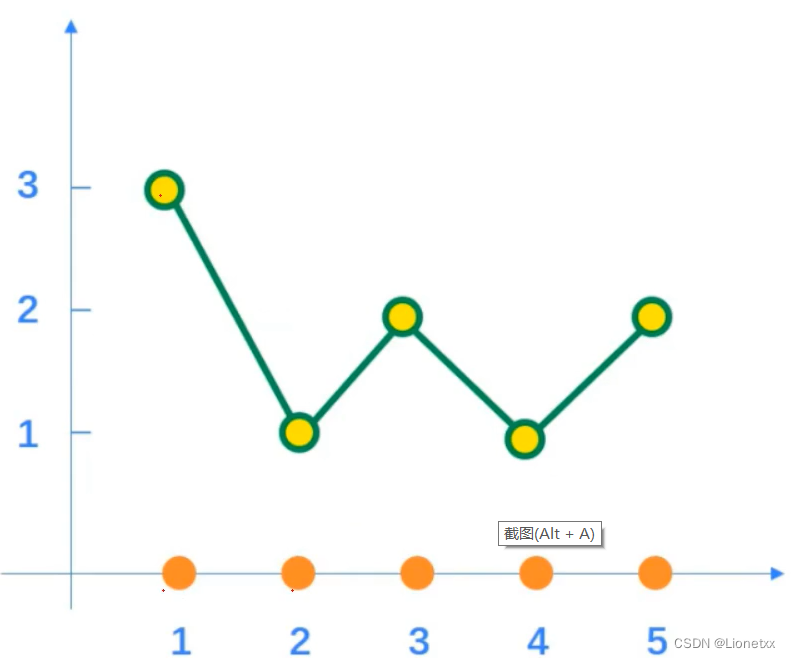
柱状图：

归一化图：

• 横坐标：图像中各个像素点的灰度级（图像中出现的像素值）
• 纵坐标：出现这个灰度级的概率（图像中每一个出现的像素值次数/像素值个数）
  

---

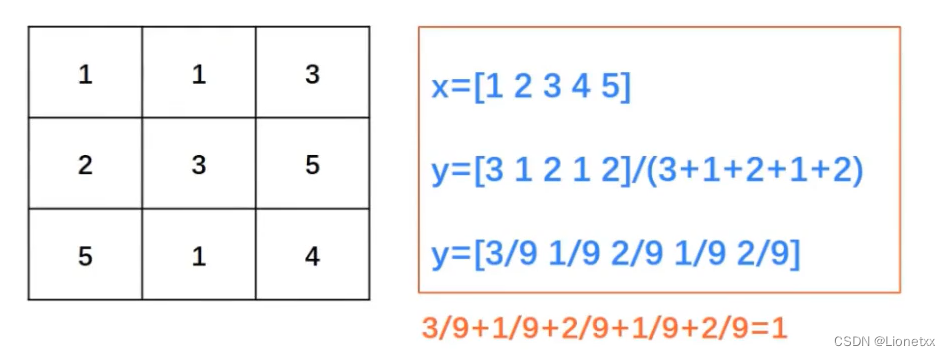
直方图术语

• dims：直方图中需要统计的特征的数目，也就是需要统计的项目。如dims = 1，表示我们只用统计灰度值
• bins：直方图中每个小区间（每个特征空间子区段）的数目，较常操作
  

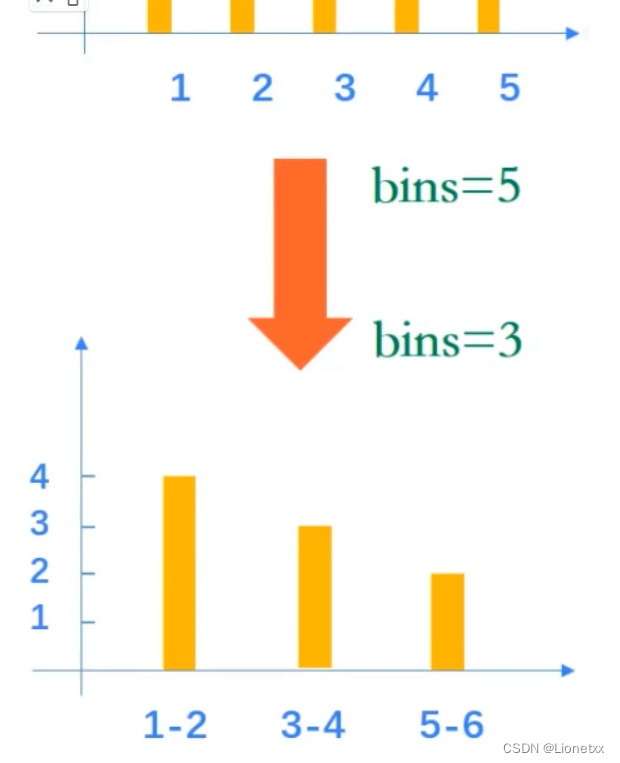
range：我们统计灰度值的范围，一般为0-255

总的来说：直方图就是图像中各种灰度级出现的次数而画出的图

---

使用OpenCV统计直方图

关键API：cv2.calcHist(images, channels, mask, histSize, ranges[, hist[, accumulate]])

• images：原始图像（可以不是黑白图），加s表示可以同时对多张图片进行直方图统计 ——> 此处要加中括号，表示是一个图像集合
• channels：指定通道，需要用中括号"[ ]"括起来
  • 如果输入的图像是灰度图，那么就只有一个通道，则[ ]内写0：[0]
  • 彩色图像可以是[ 0 ], [ 1 ], [ 2 ]，分别对应B,G,R
• mask：掩码图像
  • 统计整幅图像的直方图：设为None
  • 统计图像某个区域的直方图：需要掩码图像
• histSize：BINS（柱状图中的柱子）的数量
  • 需要用中括号括起来，如[256]（因为是从0开始，因此有256个数字）
• ranges：像素值范围，例如[0,255]
• accumulate：累积标识
  • 默认值为False（一般我们只操作一个图）
  • 如果被设置为True，则直方图在开始分配时不会被清零
  • 该参数允许从多个对象中计算单个直方图，或者用于实时更新直方图
  • 多个直方图的累积结果，用于对一组图像计算直方图
• 该函数会返回直方图的数据，可以直接用plt.plot(返回值)进行绘图！

# OpenCV统计直方图

import cv2
import numpy as np

img = cv2.imread('./lena.png')

hist = cv2.calcHist([img],[0],None,[256],[0,255])
print(hist)
1
2
3
4
5
6
7
8
9

结果：

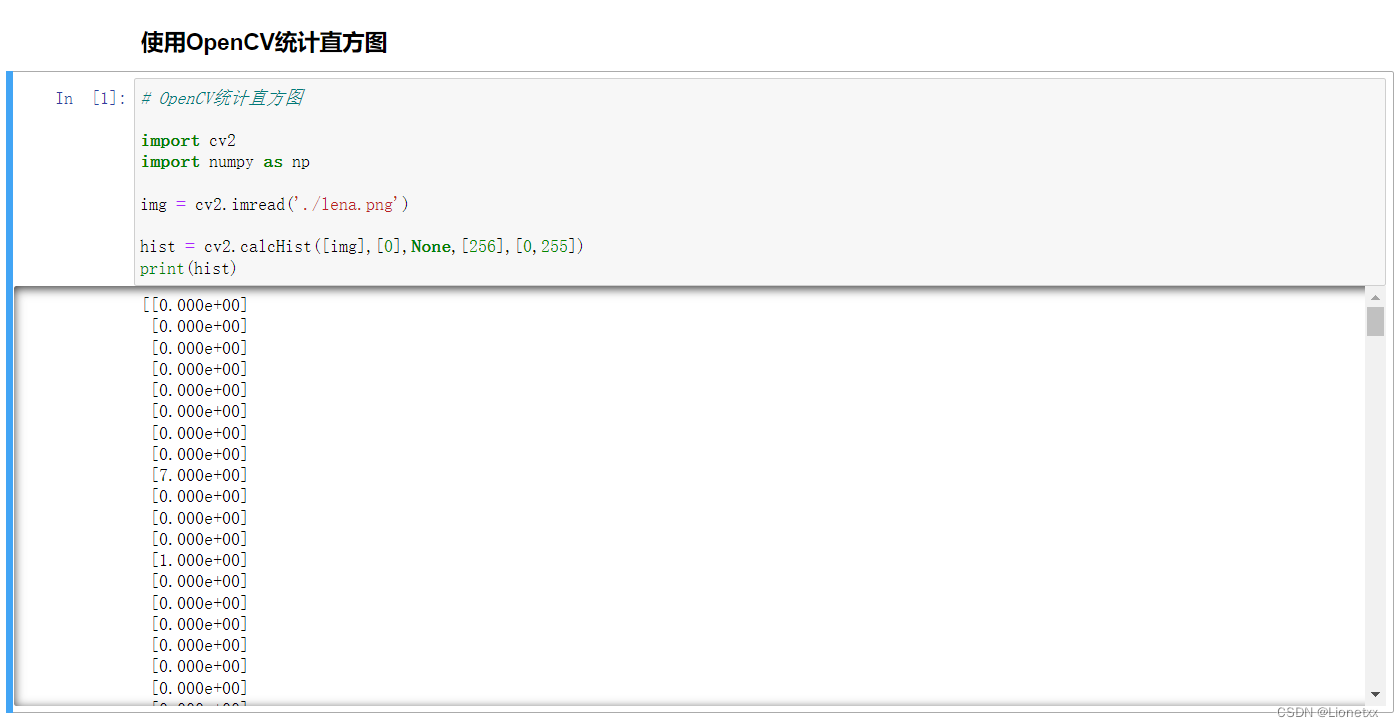
从上到下分别是灰度级0、1、2......

---

使用OpenCV绘制直方图

# 绘制直方图
# 使用Opencv的统计方法

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('./lena.png')

# 统计直方图数据，不用再去做灰度图（参数channels可以对通道进行统计）
hist_B = cv2.calcHist([img],[0],None,[256],[0,255])
hist_G = cv2.calcHist([img],[1],None,[256],[0,255])
hist_R = cv2.calcHist([img],[2],None,[256],[0,255])

# 上方得到三个数据，我们对应地画三个图，标注不同的颜色
plt.plot(hist_B,color = 'b',label = 'Blue') # 不用再用hist()，因为返回的本来就是直方图数据
plt.plot(hist_G,color = 'g',label = 'Green')
plt.plot(hist_R,color = 'r',label = 'Red')
plt.legend() # 在轴上放说明
# 展示（加不加都行）
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

结果：
对应横轴是灰度值转化来的（我们没有给定横轴的值，matplotlib自动索引的，相当于 cv2.cvtColor(img,cv2.COLOR_GRAY2BRR)）

我们可以发现：整个图都是偏红色（红色低频较少，在高频区较多），蓝色在偏低的位置（只有帽子上有一点），绿色在高频区较少（整幅图几乎没有绿色）

---

使用掩膜的直方图

如果你只对图片中的某一部分感兴趣（例如图像中的人脸、手…），就可以用掩膜进行操作，选出图中的roi区域，对该区域使用cv2.calcHist(mask)进行直方图计算

• 掩膜
  
  掩膜的特点：想要显示的区域是纯白的，其他不想让它显示的区域是纯黑的
• 如何生成掩膜
  • 先生成一个和原始图片大小一样（img.shape）的全黑图片：mask = np.zeros(image.shape,np.uint8)
  • 将想要的区域通过索引的方式设置为255：mask[100:200,200:300] = 355

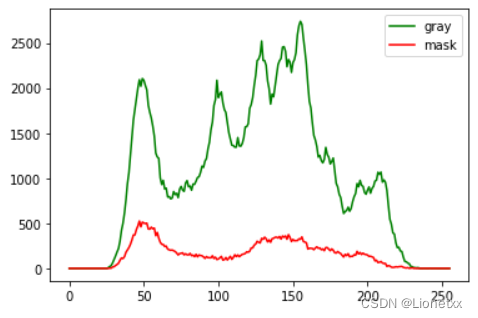
# 使用掩膜的直方图

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('./lena.png')

# 变成黑白的图
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)  

# 生成掩膜图像
mask = np.zeros(gray.shape,np.uint8) # 生成和原图大小一样的全黑图 uint8：8位全部用来表示数字

# 设置想要统计直方图的区域(roi)
mask[200:400,200:400] = 255

# 统计直方图数据 ——> 拿原图和进行掩膜操作后的数据进行对比
hist_gray = cv2.calcHist([gray],[0],None,[256],[0,255])
hist_mask = cv2.calcHist([gray],[0],mask,[256],[0,255])

# 使用matplotlib画出直方图
plt.plot(hist_gray,label = 'gray',color = 'g')
plt.plot(hist_mask,label = 'mask',color = 'r')
plt.legend()
plt.show()

##---------------------------------------------------------------------------------------------
# 我们想提前看一下掩膜在图片中的作用效果
cv2.imshow('gray',gray)
cv2.imshow('mask',mask)

# gray 和 gray 与运算的结果还是本身  mask的作用：前面先做与运算，结果再和mask做与运算
# 与运算的特点：两个数相“与”，0与任何数都是0，255和非0的“与”都是非0本身（原图）
cv2.imshow('gray&mask',cv2.bitwise_and(gray,gray,mask = mask))
##---------------------------------------------------------------------------------------------

# 退出条件
cv2.waitKey(0)
cv2.destroyAllWindows()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

结果：