一个无向图G 的最小生成树(minimum spanning tree) 就是由该图的那些连接 G 的所有顶点的边构成的树，即在最小生成树中边的条数为 |V| - 1，且其总的值最低。最小生成树存在当且仅当 G 是连通的。虽然一个强壮的算法应该指出 G 不连通的情况，但是我们还是假设 G 是连通的。

对于最小生成树问题，贪婪的做法是成立的，这里介绍两种算法，它们的区别在于最小（值的）边如何选取上。

Prim 算法

在该算法的任一时刻，我们都可以看到一组已经添加到树中的顶点，而其余顶点尚未加到树上。此时，算法在每一阶段都可以通过选择边(u, v)，使得(u, v) 的值是所有 u 在树上但 v 不在树上的边的最小值，从而找出一个新的顶点并将它添加到这棵树中。

图1 无向图G

对于图1 中的无向图 G，图2 指出了该算法如何从 v₁ 开始构建最小生成树。开始时，v₁ 在构建中的树上，它作为树的根但是没有边。每一步添加一条边和一个顶点到树上。

图2 在每一步之后的 Prim 算法

我们可以看到，Prim 算法基本上与求最短路径的 Dijkstra 算法相同。因此，和前面一样，我们对每一个顶点保留值 d_v 和 p_v 以及一个指标，标示该顶点是 known 的还是 unknown 的。这里，d_v 是连接 v 到一个 known 顶点的最短边的权，而 p_v 则是导致 d_v 改变的最后的顶点。算法其余部分完全一样，只有一点不同：由于 d_v 的定义不同，因此它的更新法则也不同：在每一个顶点 v 被选取之后，对于每一个邻接到 v 的unknown 的 w，d_w = min(d_w, v_w,v)。

表的初始配置由图3 指出，其中 v₁ 被选取，而 v₂、v₃、v₄ 被更新。结果如图4 所示。

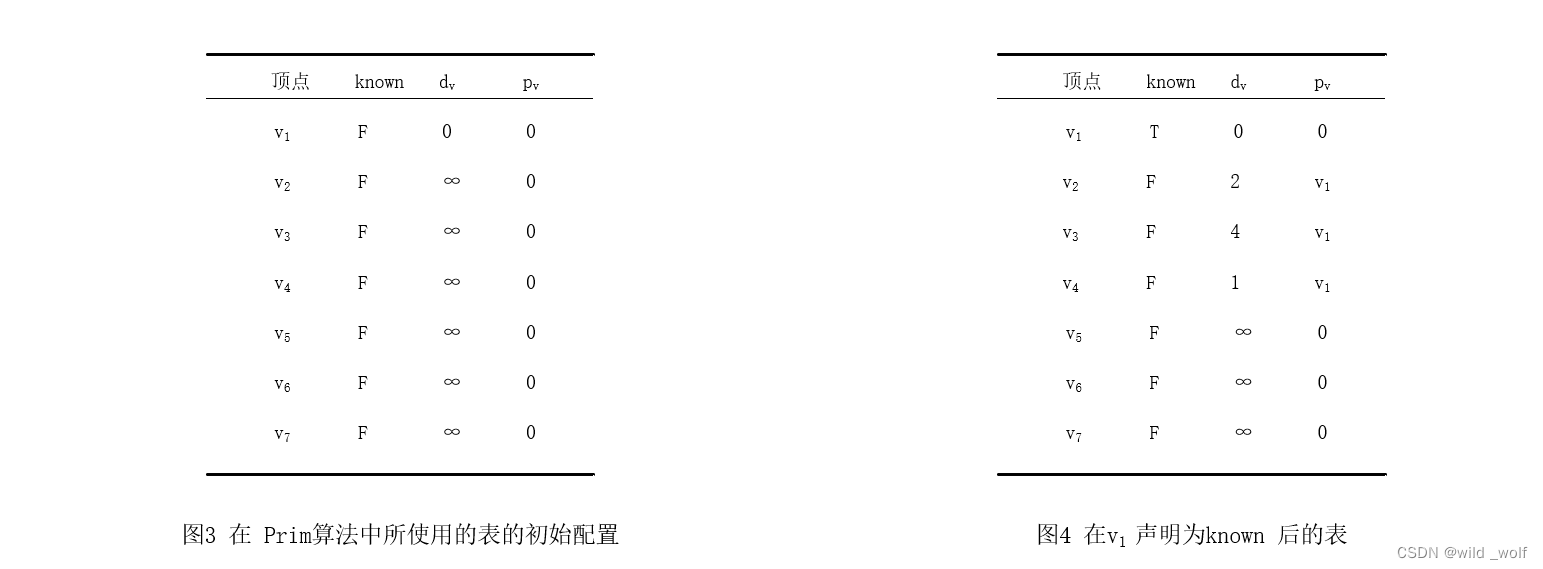
下一个顶点选择 v₄，每个顶点都邻接到它，除开 known 的v₁。v₂ 不变，因为它的 d_v = 2 而从 v₄ 到 v₂ 的边值为3，其他所有顶点都被更新。

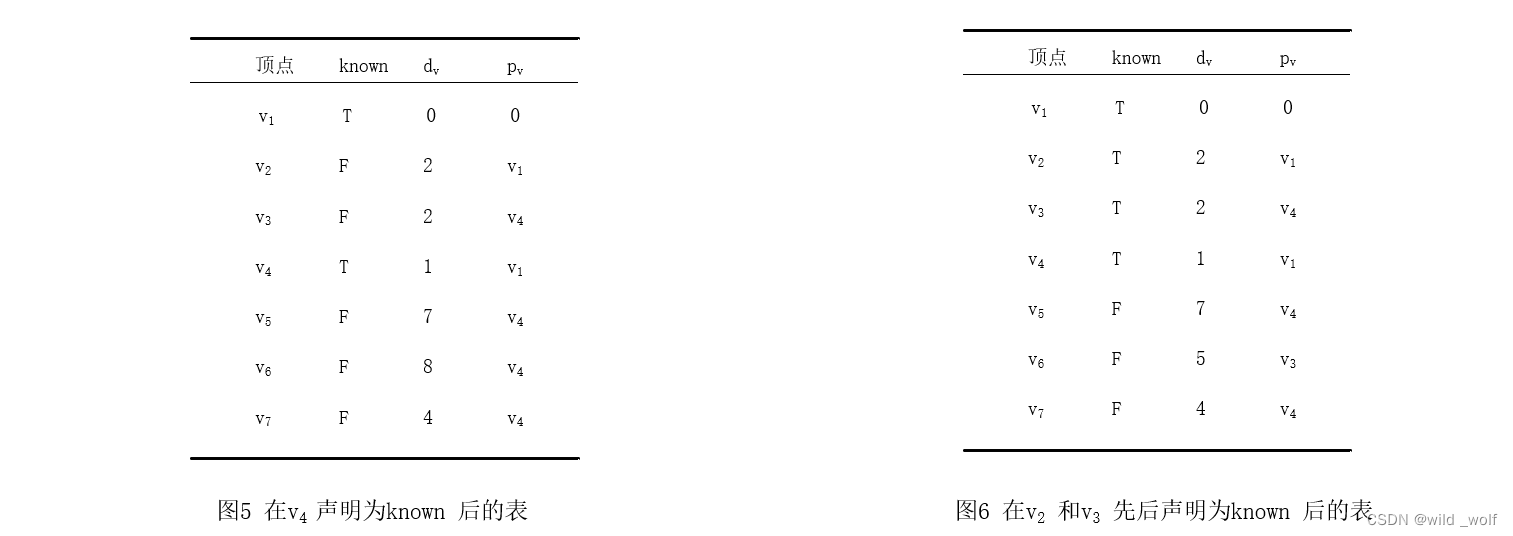
下一个选取 v₂，它并不影响距离。然后选取 v₃，其影响 v₆ 中的距离，如图6 所示。然后选取 v₇ 得到图7 ，v₆ 和 v₅ 需要做相应的调整。然后选取 v₆ 再选 v₅，算法完成。

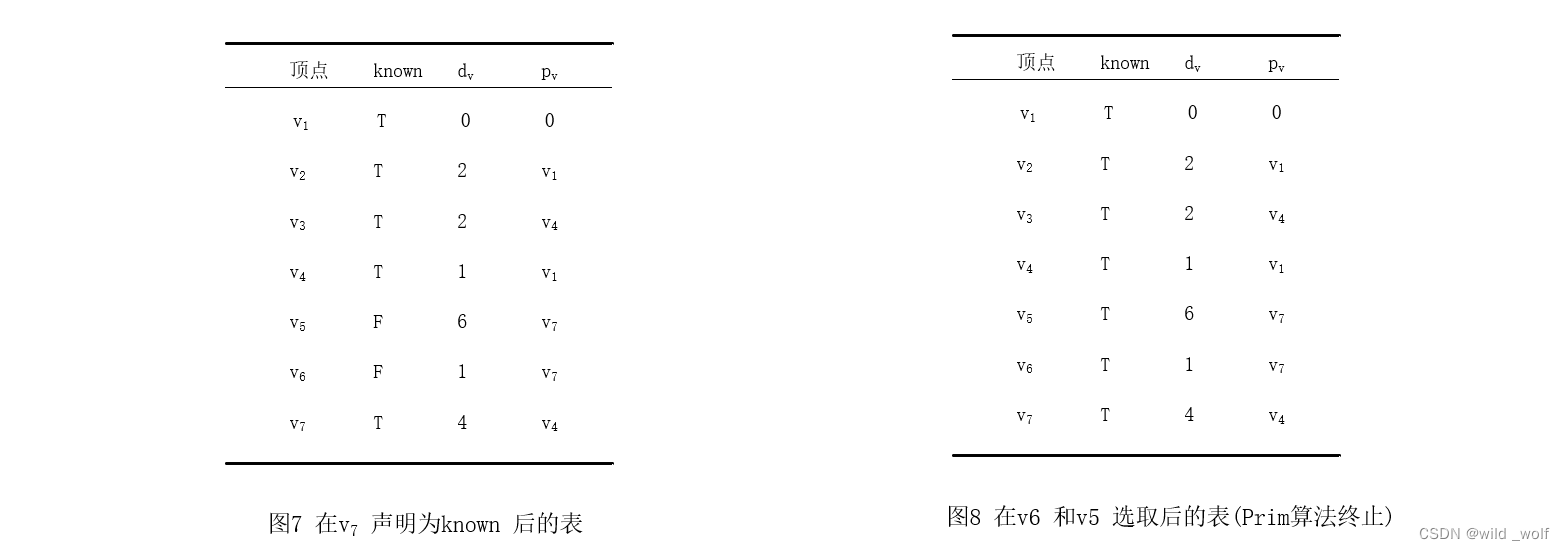
最后的表由图8 给出，生成树的边可以从该表中读出：(v₂, v₁), (v₃, v₄), (v₄, v₁), (v₅, v₇), (v₆, v₇), (v₇, v₄)。生成树的总值为16。

该算法整个的实现实际上和 Dijkstra 算法的实现是一样的，对于 Dijkstra 算法分析所做的一切都可以用到这里。不过要注意，Prim 算法是在无向图上运行的，因此当编写代码的时候要记住把每一条边放到两个邻接表中。不用堆时的运行时间为 O(|V|²)，它对于稠密图来说是最优的。使用二叉堆的运行时间是 O(|E|log|V|)，对于稀疏图它是一个好的界。

Kruskal 算法

第二种贪婪策略是连续地按照最小权的顺序选择边，并且当所选的边不产生圈时就把它作为所取定的边。该算法对前面例子中的图的实施过程如图8 所示。

形式上，Kruskal 算法 是在处理一个森林——树的集合。开始的时候，存在 |V| 棵单节点树，而添加一边则将两棵树合并成一棵树。当算法终止时就只有一棵树了，这棵树就是最小生成树。图9 显示了边被添加到森林中的顺序。

图9 在每一步之后的 Kruskal 算法

算法在足够的边被添加进来时终止。实际上，算法就是要决定边 (u, v) 应该添加还是应该放弃。不相交集类中的 union/find 算法是适用于这里的数据结构。

在 Kruskal 算法实施的任一时刻，两个顶点属于同一集合当且仅当它们在当前的生成树中连通。 因此，每个顶点最初是在它自己的集合中。如果 u 和 v 在同一个集合中，那么连接它们的边就要放弃，因为由于它们已经连通了，再添加边 (u, v) 就会形成一个圈。反之，则将它们的边加入，并对包含顶点 u 和 v 的这两个集合实施一次 union。容易看到，这样将保持集合的不变性，因为一旦边 (u, v) 添加到生成森林中，若 w 连通到 u 而 x 连通到 v，则 x 和 w 必然是连通的，因此属于相同的集合。最后，用线性时间建立一个堆将边排序可便于选取。

该算法的最坏情形运行时间为 O(|E|log|E|)，它受堆操作控制。由于|E|=O(|V|²)，因此这个运行时间时间上是 O(|E|log|V|)，在实践中该算法要比这个时间界指示的时间快得多。

Kruskal 算法的伪代码：

vector<Edge> kruskal(vector<Edge> edges, int numVertices)
{
	DisjSets ds{ numVertices };
	priority_queue pq{ edges };
	vector<Edge> mst;

	while (mst.size() != numVertices - 1)
	{
		Edge e = pq.pop();	//边 e = (u, v)
		SetType uset = ds.find(e.getu());
		SetType vset = ds.find(e.getv());

		if (uset != vset)
		{
			//接受该边
			mst.push_back(e);
			ds.union(uset, vset);
		}
	}
	return mst;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21