内点法（interior point method）求解二次规划，附python代码

 内点法介绍这篇博文写的很好https://blog.csdn.net/dymodi/article/details/46441783，在这篇文章的基础上，本文给出障碍函数法代码和一个算例。

障碍函数内点法的主要思想是：把不等式约束放进目标函数里。以下面的问题为例

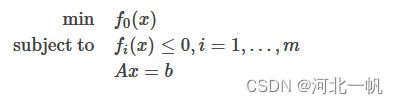
 不等式约束放进目标函数，变成如下形式：

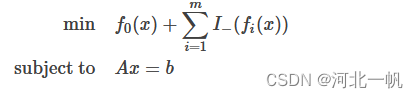
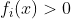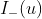当 时，函数特别大，我们希望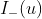这个函数像下图红虚线的样子，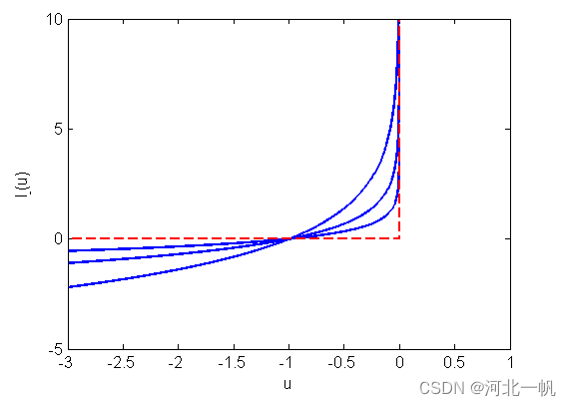

但那样不可导，所以我们用如下形式的函数去近似。

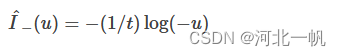
图中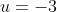，时由下往上的的3根蓝线，对应的值是依次增大。障碍函数内点法在迭代的时候，t初值给一个小值，t逐渐增大，使可行域越来越接近红虚线。

在 t 的每一步迭代中，原问题转化为如下子问题：

 

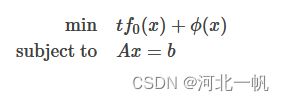
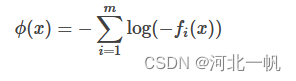
求解子问题，得到一个最优解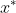，这个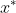是 t 下一步迭代的x初值。

子问题的求解可以用拉格朗日乘子法。

 

拉格朗日乘子法中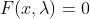，通过牛顿迭代法（Newton-Raphson method）求解。

牛顿迭代法解非线性方程组

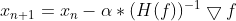
H(f)是Hessian矩阵。

得到子问题的最优解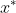，然后继续迭代 t

 障碍函数内点法的算法步骤如下：（节选自Stephen Boyd的《Convex Optimization》）

 迭代终止条件中的m就是不等式约束的个数那个m，为什么以这个条件为终止的原因，参见文章开头提到的博客，Boyd的书里也有详细的证明，是通过原问题的对偶问题证明得到的。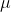是一个大于0的参数，使t每次迭代增大。

 算例：

求解如下二次规划问题（解为 x1=0.5，x2=2.25）：

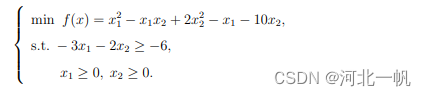
 转化为如下子问题：

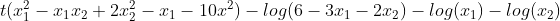
 完整python代码如下：

import numpy as np
import time
 
 
def grad_f(t, x1, x2):
    return np.array([[t * (2 * x1 - x2 - 1) + 3 / (6 - 3 * x1 - 2 * x2) - 1 / x1],
                    [t * (-1 * x1 + 4 * x2 - 10) + 2 / (6 - 3 * x1 - 2 * x2) - 1 / x2]])
 
 
def Hessian_f(t, x1, x2):
    return np.array([[2*t - 9 / pow((6-3*x1-2*x2), 2) + 1 / pow(x1, 2), -t - 6 / pow((6-3*x1-2*x2), 2)],
                    [-t - 6 / pow((6-3*x1-2*x2), 2), 4*t - 4 / pow((6-3*x1-2*x2), 2) + 1 / pow(x2, 2)]])
 
 
def NewtonRaphson(t, x1, x2):
    gf = grad_f(t, x1, x2)
 
    Hf = Hessian_f(t, x1, x2)
    Hf_inv = np.linalg.inv(Hf)
 
    deltaX = 0.1 * np.matmul(Hf_inv, gf)
    res = np.linalg.norm(deltaX, 2)
 
    return x1 - deltaX[0, 0], x2 - deltaX[1, 0], res
 
 
if __name__ == "__main__":
    time_start = time.time()
    t = 2
    x1 = 1
    x2 = 2
    while True:
        while True:
            x1, x2, res = NewtonRaphson(t, x1, x2)
            if res < 0.0001:
                break
 
            # print(x1, x2, res)
            # print("------")
 
        if 3.0 / t < 0.0001:
            time_end = time.time()
            print('consume time:', time_end - time_start)
            print("t:{}, x1:{}, x2:{}".format(t, x1, x2))
            break
        t = 2 * t