六大排序算法（Java版）：从插入排序到快速排序（含图解）

目录

插入排序 (Insertion Sort)

直接插入排序的特性总结：

选择排序 (Selection Sort)

直接选择排序的特性总结

冒泡排序 (Bubble Sort) 

冒泡排序的特性总结

堆排序（Heap Sort）

堆排序的特性总结

希尔排序 (Shell Sort) 

 希尔排序的特性总结

快速排序（Quick Sort）

Hoare版

 挖坑法

 前后指针

快速排序总结

总结

---

在计算机科学中，排序是一个基本的算法问题。排序算法可以将一组数据按照一定的顺序排列，这有助于提高搜索、查找和其他操作的效率。本文将介绍六种常见的排序算法，包括插入排序、希尔排序、选择排序、冒泡排序、堆排序和快速排序，每种算法都有其独特的特点和适用场景。

插入排序 (Insertion Sort)

插入排序是一种简单直观的排序算法，它逐步构建有序序列。它的工作原理是从未排序部分取出一个元素，将其插入到已排序部分的适当位置。插入排序的时间复杂度为O(n^2)，适用于小型数据集。就像我们玩扑克牌一样~~😁

动画演示：

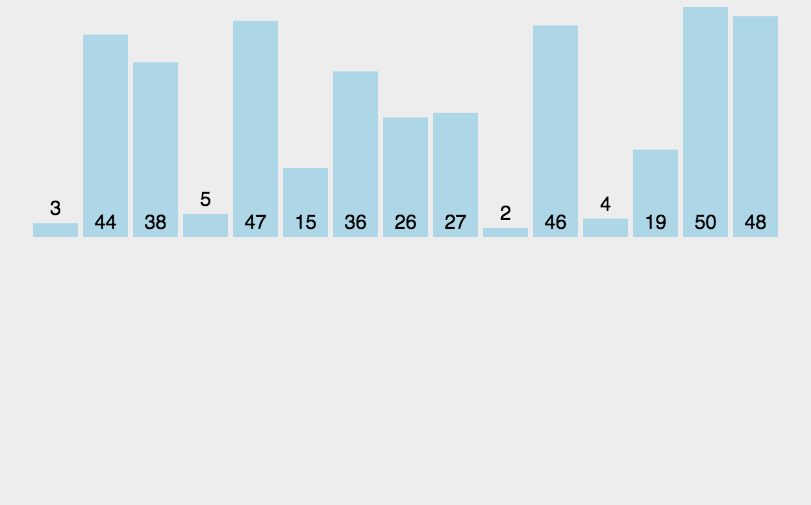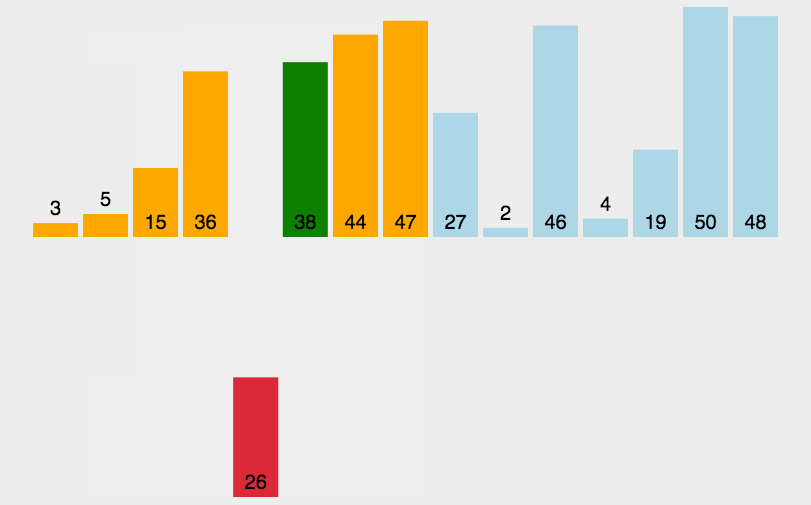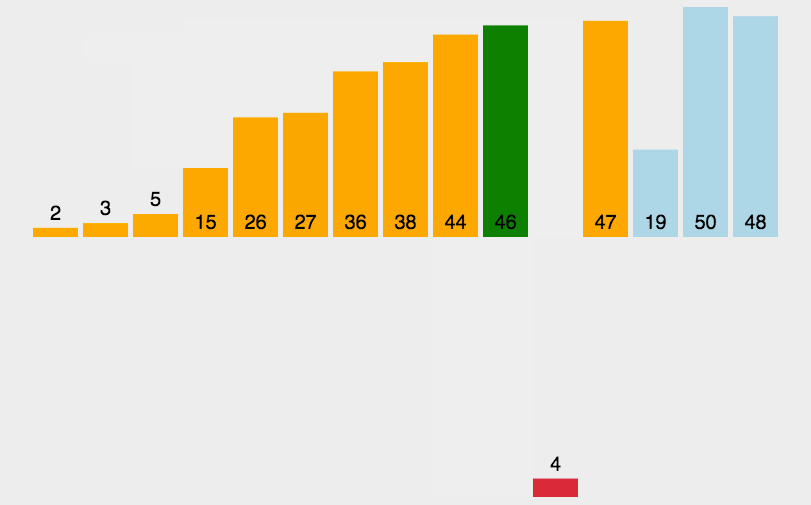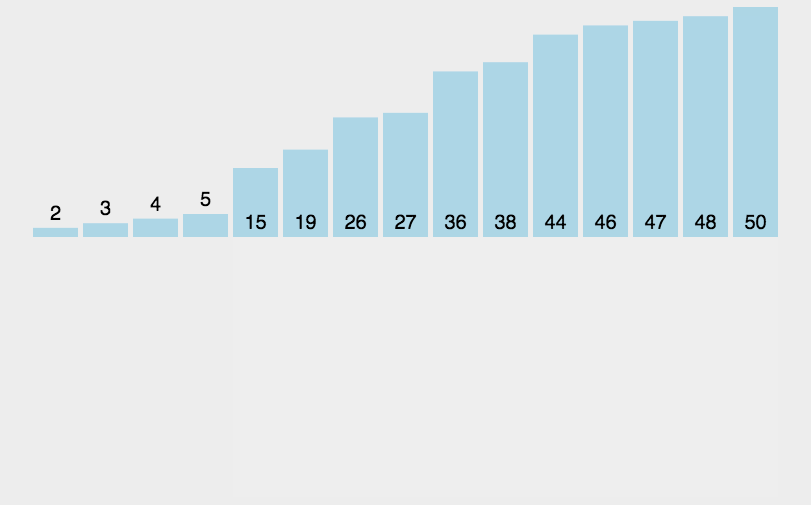
代码示例：

public static void insertionSort(int[] arr) {
        int n = arr.length;
        for (int i = 1; i < n; i++) {
            int key = arr[i];
            int j = i - 1;
 
            while (j >= 0 && arr[j] > key) {
                arr[j + 1] = arr[j];
                j--;
            }
            arr[j + 1] = key;
        }
    }

插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

直接插入排序的特性总结：

1. 元素集合越接近有序，直接插入排序算法的时间效率越高

2. 时间复杂度：O(N^2)

3. 空间复杂度：O(1)，它是一种稳定的排序算法

4. 稳定性：稳定

选择排序 (Selection Sort)

选择排序一种简单但低效的排序算法。它的工作原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。 

动画演示：

代码示例：

public static void selectionSort(int[] arr) {
        int n = arr.length;
        for (int i = 0; i < n - 1; i++) {
            int minIndex = i;
            for (int j = i + 1; j < n; j++) {
                if (arr[j] < arr[minIndex]) {
                    minIndex = j;
                }
            }
            int temp = arr[minIndex];
            arr[minIndex] = arr[i];
            arr[i] = temp;
        }
    }

直接选择排序的特性总结

1. 直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用

2. 时间复杂度：O(N^2)

3. 空间复杂度：O(1)

4. 稳定性：不稳定

冒泡排序 (Bubble Sort) 

冒泡排序是一种基本的交换排序算法，它重复遍历数据并比较相邻元素，如果它们的顺序不正确，则交换它们。冒泡排序的时间复杂度为O(n^2)，与选择排序一样，适用于小型数据集。

动画演示：

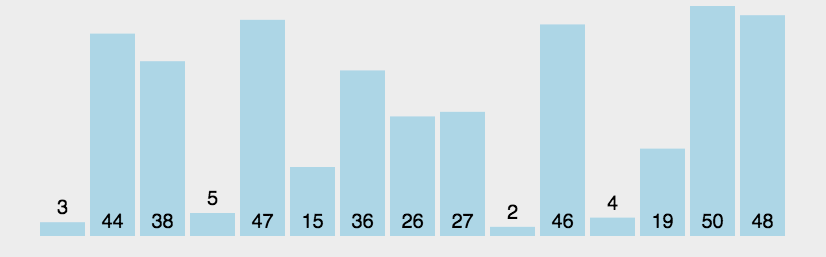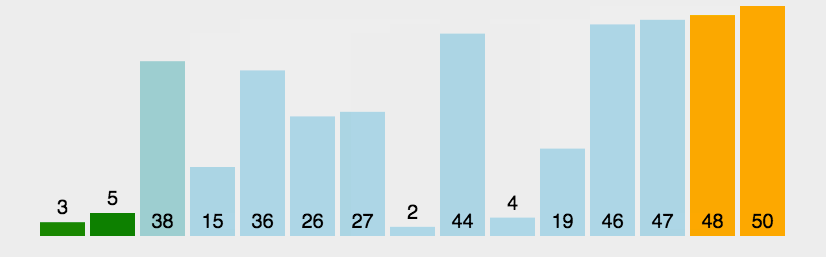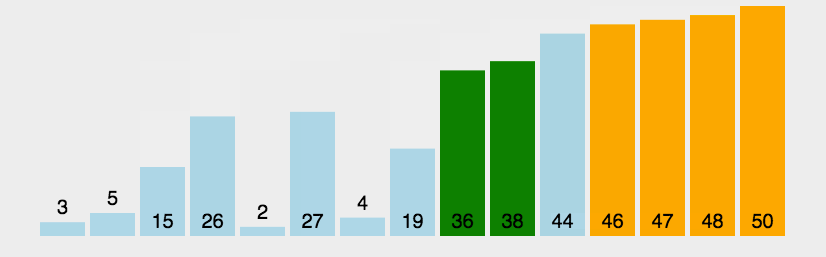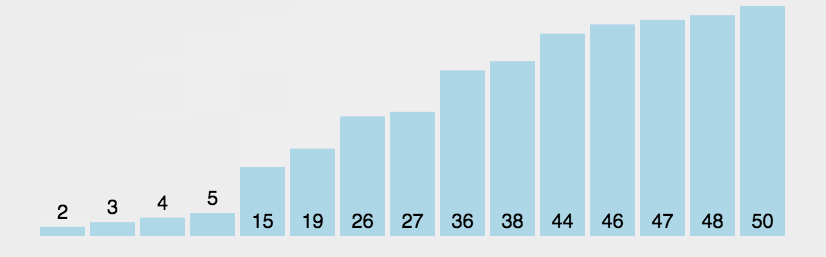
代码示例： 

public static void bubbleSort(int[] arr) {
        int n = arr.length;
        for (int i = 0; i < n - 1; i++) {
            for (int j = 0; j < n - i - 1; j++) {
                if (arr[j] > arr[j + 1]) {
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }
    }

冒泡排序的特性总结

1. 冒泡排序是一种非常容易理解的排序

2. 时间复杂度：O(N^2)

3. 空间复杂度：O(1)

4. 稳定性：稳定

堆排序（Heap Sort）

堆排序使用二叉堆数据结构来实现排序。它将待排序数据构建成一个堆，然后逐步将堆顶元素与最后一个元素交换，然后对剩余部分重新构建堆。堆排序的时间复杂度为O(nlogn)，性能较好，特别适用于大型数据集。

动画演示：

代码示例：

public class HeapSort {
    public static void heapSort(int[] arr) {
        int n = arr.length;
 
        // 构建最大堆
        for (int i = n / 2 - 1; i >= 0; i--) {
            heapify(arr, n, i);
        }
 
        // 逐个将最大元素移到末尾
        for (int i = n - 1; i > 0; i--) {
            // 交换根节点（最大值）和当前未排序部分的末尾元素
            int temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;
 
            // 对剩余部分重新构建最大堆
            heapify(arr, i, 0);
        }
    }
 
    public static void heapify(int[] arr, int n, int i) {
        int largest = i;
        int left = 2 * i + 1;
        int right = 2 * i + 2;
 
        // 找到左子节点和右子节点中的最大值
        if (left < n && arr[left] > arr[largest]) {
            largest = left;
        }
        if (right < n && arr[right] > arr[largest]) {
            largest = right;
        }
 
        // 如果最大值不是根节点，则交换根节点和最大值，并继续堆化
        if (largest != i) {
            int swap = arr[i];
            arr[i] = arr[largest];
            arr[largest] = swap;
            heapify(arr, n, largest);
        }
    }
 
    public static void main(String[] args) {
        int[] arr = {12, 11, 13, 5, 6, 7};
        heapSort(arr);
        System.out.println("堆排序结果:");
        for (int num : arr) {
            System.out.print(num + " ");
        }
    }
}

堆排序的特性总结

1. 堆排序使用堆来选数，效率就高了很多。

2. 时间复杂度：O(N*logN)

3. 空间复杂度：O(1)

4. 稳定性：不稳定

希尔排序 (Shell Sort) 

希尔排序法又称缩小增量法。希尔排序法的基本思想是：先选定一个整数，把待排序文件中所有记录分成多个组， 所有距离为的记录分在同一组内，并对每一组内的记录进行排序。然后，取，重复上述分组和排序的工作。当到达 =1时，所有记录在统一组内排好序。

动画演示：

代码示例：

public static void shellSort(int[] arr) {
        int n = arr.length;
        for (int gap = n / 2; gap > 0; gap /= 2) {
            for (int i = gap; i < n; i++) {
                int temp = arr[i];
                int j = i;
                while (j >= gap && arr[j - gap] > temp) {
                    arr[j] = arr[j - gap];
                    j -= gap;
                }
                arr[j] = temp;
            }
        }
    }

 希尔排序的特性总结

1. 希尔排序是对直接插入排序的优化。

2. 当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的对比。

3. 希尔排序的时间复杂度不好计算，因为gap的取值方法很多，导致很难去计算，因此在好些树中给出的希尔排序的时间复杂度都不固定：

快速排序（Quick Sort）

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有 元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

动画演示：

// 假设按照升序对array数组中[left, right)区间中的元素进行排序
void QuickSort(int[] array, int left, int right)
{
    if(right - left <= 1)
        return;
    // 按照基准值对array数组的 [left, right)区间中的元素进行划分
    int div = partion(array, left, right);
    // 划分成功后以div为边界形成了左右两部分 [left, div) 和 [div+1, right)
    // 递归排[left, div)
    QuickSort(array, left, div);
    // 递归排[div+1, right)
    QuickSort(array, div+1, right);
}

上述为快速排序递归实现的主框架，发现与二叉树前序遍历规则非常像，我们在写递归框架时可想想二叉树前序遍历规则即可快速写出来，后序只需分析如何按照基准值来对区间中数据进行划分的方式即可。

Hoare版

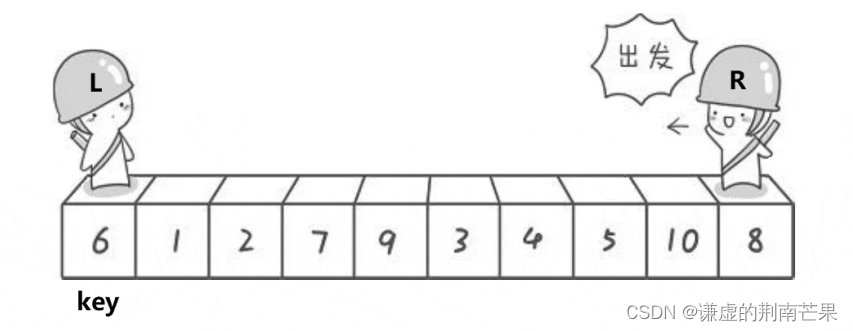
private static int partition(int[] array, int left, int right) {
    int i = left;
    int j = right;
    int pivot = array[left];
    while (i < j) {
        while (i < j && array[j] >= pivot) {
            j--;
        }
    while (i < j && array[i] <= pivot) {
            i++;
        }
    swap(array, i, j);
    }
    swap(array, i, left);
    return i;
}

 挖坑法

private static int partition(int[] array, int left, int right) {
    int i = left;
    int j = right;
    int pivot = array[left];
    while (i < j) {
        while (i < j && array[j] >= pivot) {
            j--;
        }
        array[i] = array[j];
        while (i < j && array[i] <= pivot) {
            i++;
        }
        array[j] = array[i];
    }
    array[i] = pivot;
    return i;
}

 前后指针

写法一： 

private static int partition(int[] array, int left, int right) {
    int prev = left ;
    int cur = left+1;
    while (cur <= right) {
        if(array[cur] < array[left] && array[++prev] != array[cur]) {
        swap(array,cur,prev);
        }
        cur++;
    }
    swap(array,prev,left);
    return prev;
}

写法二：

private static int partition(int[] array, int left, int right) {
    int d = left + 1;
    int pivot = array[left];
    for (int i = left + 1; i <= right; i++) {
        if (array[i] < pivot) {
            swap(array, i, d);
            d++;
        }
    }
    swap(array, d - 1, left);
    return d - 1;
}

快速排序总结

1. 快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序

2. 时间复杂度：O(N*logN)

3. 空间复杂度：O(logN)

4. 稳定性：不稳定

 

总结

在这篇博客中，我们深入探讨了六种常见的排序算法，包括插入排序、希尔排序、选择排序、冒泡排序、堆排序和快速排序。以下是对每个排序算法的简要总结：

1. 插入排序：逐步构建有序序列，适用于小型数据集，时间复杂度为O(n^2)。

2. 希尔排序：改进的插入排序，通过分组排序提高效率，平均时间复杂度为O(nlogn)。

3. 选择排序：每轮选择最小元素并放在已排序部分的末尾，适用于小型数据集，时间复杂度为O(n^2)。

4. 冒泡排序：通过交换相邻元素将最大元素逐步移动到未排序部分的末尾，适用于小型数据集，时间复杂度为O(n^2)。

5. 堆排序：使用堆数据结构实现排序，时间复杂度为O(nlogn)，适用于大型数据集。

6. 快速排序：分治排序算法，选择基准元素，将数据分为两个子数组，时间复杂度为O(nlogn)，性能良好。

每个排序算法都有其独特的特点和适用场景，选择合适的算法取决于数据规模、性能需求和具体应用场景。这些排序算法的Java示例代码和详细解释有助于理解它们的工作原理和用法。 

总之，排序算法是计算机科学中的基础知识，了解这些算法对于编写高效的程序至关重要。

下一期我会总结一下快速排序的优化方法，希望大家支持~~🤩