题目

给一个字符串s，找出s中最长的回文子串
示例1

输入： s = "babad"
输出： “bab”
解释： “aba”同样是符合题意的答案
1
2
3

示例2

输入： s = "cbbd"
输出： “bb”
1
2

思路

方法一：动态规划
  对于一个子串而言，如果它是回文串，并且长度大于2，那么将它首尾的两个字母去除之后，它仍然是个回文串。例如，对于字符串"ababa"，如果已经知道“bab”是回文串，那么“ababa”一定是回文串，因为它的首尾两个字母都是“a”.
  依照上面的思路，可以用动态规划的方法解决本题。用P(i,j)表示字符串s的第i到j个字母组成的串,用s[i:j]表示是否为回文串：

  这里的『其他情况』包含两种可能性：

• s[i,j]本身不是一个回文串
• i>j，此时s[i,j]本身不合法

  此时，就可以写出动态规划的状态转移方案：

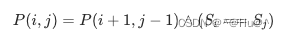
  也就是说，只有s[i+1,j+1]是回文串，并且s的第i和j个字母相同时，s[i:j]才会是回文串。
  上述所有讨论是建立在子串长度大于2的前提之上的，还需要考虑动态规划中的边界条件，即子串的长度为1或2.对于长度为1的子串，其显然是个回文串；对于长度为2的子串，只要其两个字母相同，其就是一个回文串。因此就可以写出动态规划的边界条件：

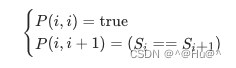
  根据这个思路，就可以完成动态规划了，最终的答案即为所有P(i,j)=true中j-i+1(即子串长度)的最大值。注意：在状态转移过程中，是从长度较短的字符串想长度较长的字符串进行转移的，因此一定要注意动态规划的循环熟顺序。

public class Solution {

    public String longestPalindrome(String s) {
        int len = s.length();
        if (len < 2) {
            return s;
        }

        int maxLen = 1;
        int begin = 0;
        // dp[i][j] 表示 s[i..j] 是否是回文串
        boolean[][] dp = new boolean[len][len];
        // 初始化：所有长度为 1 的子串都是回文串
        for (int i = 0; i < len; i++) {
            dp[i][i] = true;
        }

        char[] charArray = s.toCharArray();
        // 递推开始
        // 先枚举子串长度
        for (int L = 2; L <= len; L++) {
            // 枚举左边界，左边界的上限设置可以宽松一些
            for (int i = 0; i < len; i++) {
                // 由 L 和 i 可以确定右边界，即 j - i + 1 = L 得
                int j = L + i - 1;
                // 如果右边界越界，就可以退出当前循环
                if (j >= len) {
                    break;
                }

                if (charArray[i] != charArray[j]) {
                    dp[i][j] = false;
                } else {
                    if (j - i < 3) {
                        dp[i][j] = true;
                    } else {
                        dp[i][j] = dp[i + 1][j - 1];
                    }
                }

                // 只要 dp[i][L] == true 成立，就表示子串 s[i..L] 是回文，此时记录回文长度和起始位置
                if (dp[i][j] && j - i + 1 > maxLen) {
                    maxLen = j - i + 1;
                    begin = i;
                }
            }
        }
        return s.substring(begin, begin + maxLen);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

复杂度分析

• 时间复杂度：O(n²)，其中n是字符串的长度。动态规划的状态总数为O(n²)，对于每个状态，需要转移的时间为O(1)
• 空间复杂度：O(n²)，即存储动态规划状态需要的空间

方法二：中心扩展算法
仔细观察以下方法一种的状态转移方法：

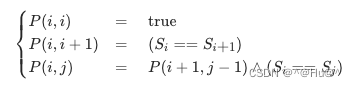
  找出其中的状态转移链：

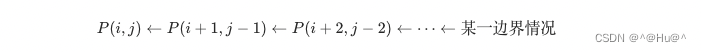
  可以发现，所有的状态在转移的时候的可能性都是唯一的。也就是说，可以从每一种情况开始「扩展」，也可以得出所有的状态对应的答案。
  边界情况即为子串长度1或2 的情况。枚举每一种边界情况，并从对应的子串开始不断的向两边扩展。如果两边的字母相同，就可以继续扩展，例如从P(i+1,j-1)扩展到P(i,j);如果两边的字母不同，就可以停止扩展，因为在这之后的子串都不能是回文串了。
  可以发现，「边界情况」对应的子串实际上就是「扩展」出的回文串的「回文中心」。方法二的本质即为：枚举所有的「回文中心」并尝试扩展，直到无法扩展为止，此时的回文串长度即为此「回文中心」下的最长回文串长度。对所有的长度求出最大值，即可得到最终的答案。

class Solution {
    public String longestPalindrome(String s) {
        if (s == null || s.length() < 1) {
            return "";
        }
        int start = 0, end = 0;
        for (int i = 0; i < s.length(); i++) {
            int len1 = expandAroundCenter(s, i, i);
            int len2 = expandAroundCenter(s, i, i + 1);
            int len = Math.max(len1, len2);
            if (len > end - start) {
                start = i - (len - 1) / 2;
                end = i + len / 2;
            }
        }
        return s.substring(start, end + 1);
    }

    public int expandAroundCenter(String s, int left, int right) {
        while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
            --left;
            ++right;
        }
        return right - left - 1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

复杂度分析

• 时间复杂度：O(n²),其中n是字符串的长度。长度为1和2的回文中心分别是n和n-1个，每个回文中心最多是会向外扩展O(n)次。
• 空间复杂度：O(1)

方法三：Manacher算法
  一个复杂度为O(n)的Manacher算法。然而本身算法非常复杂，一般不作为面试内容。
  定义一个新概念 臂长,表示中心扩展算法向外扩展的长度。如果一个位置的最大回文字符串长度为2*length+1，其臂长为length。
  长度为奇数的回文字符串
  在中心扩展算法的过程中，能够得出每个位置的臂长。当要得出以下一个位置i的臂长时，能不能利用之前得到的信息呢？
  答案是肯定的。具体来说，如果位置j的臂长为length，并且有i_length>1,如下图所示：

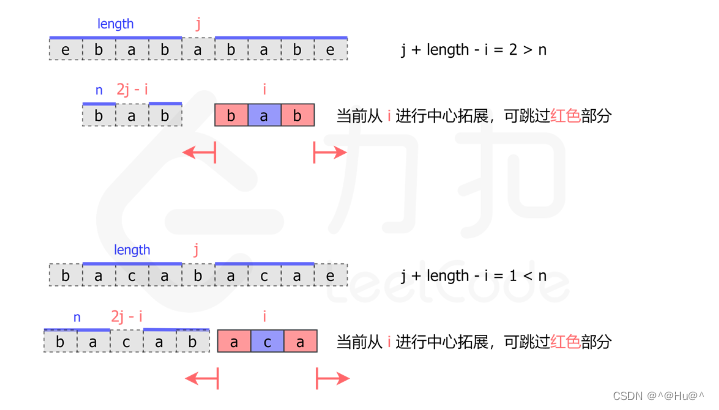
  当在位置i开始进行中心扩展时，可以先找到i关于j的对称点2*j-1。那么如果点2*j-1的臂长等于n，就可以知道，点i的臂长至少为min(j+length-i,n).那么就可以直接跳过i到i+min(j+legth-i,n)这部分，从i+min(i+length-1,n)+1开始扩展。
  只需要在中心扩展法的过程中记录右臂在最右边的回文字符串，将其中心作为j，在计算过程中就能最大限度的避免重复计算。
  长度为偶数的回文字符串
  通过一个特别的操作将奇偶数的情况统一起来：向字符串的头尾以及每两个字符中间添加一个特殊字符#,比如字符串aaba,处理后会变成#a#a#b#a#。那么原先长度为偶数的回文字符串aa会变成长度为奇数的回文字符串#a#a#，而长度为奇数的字符串aba会变成长度仍然为奇数的回文字符串#a#b#a#，就不需要再考虑长度为偶数的回文字符串了。
  注意这里的特殊字符不需要是没有出现过的字母，可以使用人格一个字符在作为这个特殊字符。这是因为当只考虑长度为奇数的回文字符串时，每次比较的两个字符奇偶数一定是相同的，所以原来字符串中的字符不会与插入的特殊字符胡相比较，不会因此产生问题。

class Solution {
    public String longestPalindrome(String s) {
        int start = 0, end = -1;
        StringBuffer t = new StringBuffer("#");
        for (int i = 0; i < s.length(); ++i) {
            t.append(s.charAt(i));
            t.append('#');
        }
        t.append('#');
        s = t.toString();

        List<Integer> arm_len = new ArrayList<Integer>();
        int right = -1, j = -1;
        for (int i = 0; i < s.length(); ++i) {
            int cur_arm_len;
            if (right >= i) {
                int i_sym = j * 2 - i;
                int min_arm_len = Math.min(arm_len.get(i_sym), right - i);
                cur_arm_len = expand(s, i - min_arm_len, i + min_arm_len);
            } else {
                cur_arm_len = expand(s, i, i);
            }
            arm_len.add(cur_arm_len);
            if (i + cur_arm_len > right) {
                j = i;
                right = i + cur_arm_len;
            }
            if (cur_arm_len * 2 + 1 > end - start) {
                start = i - cur_arm_len;
                end = i + cur_arm_len;
            }
        }

        StringBuffer ans = new StringBuffer();
        for (int i = start; i <= end; ++i) {
            if (s.charAt(i) != '#') {
                ans.append(s.charAt(i));
            }
        }
        return ans.toString();
    }

    public int expand(String s, int left, int right) {
        while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
            --left;
            ++right;
        }
        return (right - left - 2) / 2;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

复杂度分析

• 时间复杂度： O(n),其中n是字符串的长度。由于对于每个位置，扩展要么从当前的最右侧臂长right开始，要么只会进行一步，而right最多向前走O(n)步，因此算法的复杂度为O(n)
• 空间复杂度：O(n),需要O(n)的空间记录每个位置的臂长。

• 练习代码

public class Test_6 {
   public static String longestPalindrome(String s) {
       int len = s.length();
       if (len<2){
           return s;
       }
       int maxLen = 1;
       int begin = 0;
       //表示是否是回文字符串
       boolean[][] dp = new boolean[len][len];
       for (int i = 0; i < len; i++) {
           //初始化，所有长度为i的字符串都是回文
           dp[i][i] = true;
       }

       char[] charArray = s.toCharArray();
       //枚举子串长度
       for (int i = 2; i <=len; i++) {
           for (int j = 0; j <len; j++) {
               //k为右边界
               int k = j+i-1;
               if (k>=len){
                   break;
               }
               if (charArray[j]!=charArray[k]){
                   dp[j][k]=false;
               }else {
                   if (k-j<3){
                       dp[j][k]=true;
                   }else {
                       dp[j][k] = dp[j+1][k-1];
                   }
               }
               //只要dp[j][k]为true，表示子串s[j...k]为回文，记录回文长度和起始位置
               if (dp[j][k]&&k-j+1>maxLen){
                   maxLen = k-j+1;
                   begin=j;
               }
           }
       }
       return s.substring(begin,begin+maxLen);
   }

   public static void main(String[] args) {
       System.out.println(longestPalindrome("cbbd"));
   }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48