叉乘分配律的几何证明

证明 $A\times (B+C)=A\times B+A\times C$

首先，把$B,C,B+C$投影到与$A$垂直的平面上，分别得到$B^{\prime },C^{\prime },(B+C{)}^{\prime }$,显然$(B+C{)}^{\prime }=B^{\prime }+C^{\prime }$.

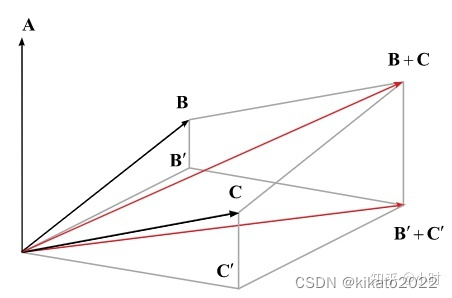
根据叉乘的定义
$|A\times B|=|A||B|sin{\theta }_{AB}=|A||B^{\prime }|=|A\times B^{\prime }|$，且 $A\times B$ 与 $A\times B^{\prime }$ 的方向相同。

所以$A\times B=A\times B^{\prime }$

同理$A\times C=A\times C^{\prime }$, $A\times (B+C)=A\times (B^{\prime }+C^{\prime })$

只需要证明 $A\times (B^{\prime }+C^{\prime })=A\times B^{\prime }+A\times C^{\prime }$ 即可
由于$B^{\prime },C^{\prime },B^{\prime }+C^{\prime }$都在与$A$垂直的平面上，所以$A$与它们叉乘的效果相当于$B^{\prime },C^{\prime },B^{\prime }+C^{\prime }$的模长分别乘以$|A|$，方向是绕$A$旋转90°。显然，把$B^{\prime },C^{\prime },B^{\prime }+C^{\prime }$都旋转90°，这个加法仍然成立。