详解深度学习中，如何进行反向传播

为什么要反向传播？

通过正向传播求初基于输入x的y_pred后，需要通过比较y_pred和原数据y，得到损失函数（一般是它们差值的L2范数）
然后，各个权重矩阵就可以根据损失函数反向传播回来的梯度进行学习更新，从而使得下一轮的损失函数更小
总的来说，反向传播起到一个提高训练模型精确度的作用

对于特定的计算图和神经网络

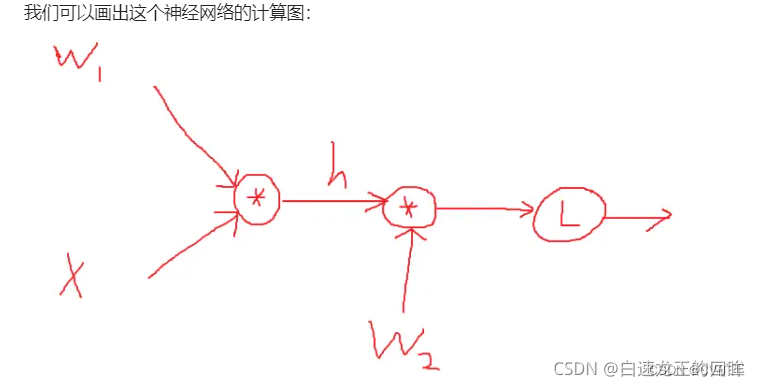
这里我们使用一个包含1层输入层，1层隐含层，1层输出层的神经网络模型
但在数量上，我们稍作变化，我们假定输入层有1000个节点，隐藏层有100个节点，输出层有10个节点，并且隐藏层使用一下sigmod激活函数（更接近实际）
这其实就相当于我们把一个人的体内1000种化学元素的含量以及他10个器官的健康状况给出
我们通过1000个化学元素的含量尝试预测这10个器官的健康状况

import numpy as np

# numpy构建神经网络
# N为训练数据个数，D_in为输入层大小，H为隐藏层大小，D_out为输出层大小
# 我们定义一个输入层为1000维向量，隐藏层为100个神经元，输出层层10个神经元的神经网络
batch_size, D_in, H, D_out =64, 1000, 100, 10

# 随机创建训练数据
x = np.random.randn(D_in, batch_size)
y = np.random.randn(D_out, batch_size)

# 根据我们的模型，包含2个权重层，分别为100个神经元的隐藏层和10个神经元的输出层
w1 = np.random.randn(H, D_in) # 隐藏层
w2 = np.random.randn(D_out, H) # 输出层

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

目前我们相当于说有64个人，每个人都有1000个化学元素的含量表，同时我们也掌握了每个人10个器官的健康状态
我们首先表示每个矩阵的行列数（方便后续反向传播的式子证明）
X：(1000,64), 表示64个人的1000个化学元素含量表
Y：(10,64)，表示64个人的10个器官的真实健康状态
w1:(100,1000)，表示由输入层到隐藏层的转换（权重）矩阵
w2:(10,100)，表示由隐藏层到输出层的转换（权重）矩阵
我们的task就是不停地让w1和w2梯度下降，从而使得loss减少

lr = 1e-5
for t in range(3000):
    # 进行前向传播
    h = w1.dot(x) # 输出数据传入隐藏层
    h_sigmod = 1 / (1 + np.exp(-h))
    y_pred = w2.dot(h_sigmod) # 隐藏层输出的数据进入输出层
    
    # 计算损失函数
    loss = np.square(y_pred - y).sum()
    if t == 1 or t == 2999:
        print("\r epoch={} loss={}".format(t, loss))
    
    # 反向传播
    grad_y_pred = 2.0 * (y_pred - y) # 首先Loss对输出数据求导，这个结果将是输出层的上游梯度,对应于公式的 2q
    
    grad_w2 = grad_y_pred.dot(h.T) # 这里计算Loss对输出层w2的偏导数，上游梯度为grad_y_pred，local gradient为h，对应于公式的2qx^T
    
    # 为了计计算Loss对w1的偏导数，W1*x中的本地偏导数很容易得到是X^T，但是还需要求得上一层传播过来的上游偏导数
    grad_sigmod = w2.T.dot(grad_y_pred) # 
    
    # 
    grad_h = grad_sigmod*(h_sigmod*(1-h_sigmod))
    
    grad_w1 = grad_h.dot(x.T) # 最后计算Loss对隐藏层w1的偏导数，上游梯度为grad_h，，local gradient为x，对应于公式的2qx^T
    
    # 执行梯度下降
    w1 -= lr * grad_w1
    w2 -= lr * grad_w2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

lr表示学习率，也就是下降的力度，而梯度就表示下降的方向
然后进行3000轮的学习
首先我们得到隐藏层的输入h 也就是w1x得到的矩阵大小就是(100,64)
然后我们对其进行sigmod变换得到h_sigmod，矩阵大小也是(100,64)
最后我们得到隐藏的输出y_pred = w2(h_sigmod)也就是(10,64)
好的，到此为止，一次正向传播就搞定了

接下来到了loss计算阶段，这个就比较好理解，它这个就是把所有人在所有器官上的预测差值求平方和即可
下面的输出是方便我们比较第1轮训练和第3000轮训练的损失结果差异的：

可以发现，这个反向传播+梯度下降确确实实是可以使得我们的训练模型变得精确起来

下面就是最繁琐的梯度（偏导数）计算环节：

反向传播本质就是对每一个权重矩阵求偏导（但在这过程中必然会涉及到其它变量的求偏导）

grad_y_pred = 2.0 * (y_pred - y) 矩阵大小(10,64)
这个就是直接对损失函数求导，就比较好理解啦

grad_w2 = grad_y_pred.dot(h.T)
这里我们的梯度肯定要和原矩阵保持一致的，也就是说我们必然知道grad_w2大小为(10,100)
然后在隐藏节点对w2的偏导就是h_sigmod(10,64)，但换成h的话下降的效果会更好
因此我们就可以通过grad_y_pred(10,64) 和 h(100,64)得到grad_w2(10,100),也只有一种方法可以乘出来

总结来说就是
当前变量（某节点输入）的偏导 = 反向传过来（某节点输出）的偏导 * 本节点对该变量的偏导

数学例子

代码：

import torch

x = torch.tensor([5.0, 7.0], requires_grad=True)
y = x**2

loss1 = torch.mean(y)

h1 = torch.autograd.grad(y[0], x, retain_graph = True, create_graph=True)
h2 = torch.autograd.grad(y[1], x, retain_graph = True, create_graph=True)
loss2 = torch.mean(h1[0] - h2[0])

loss = loss1 + loss2

result = torch.autograd.grad(loss, x)
print(result)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16