概要

单调栈，思考起来比较费劲。

题目

给定非负整数数组 heights ，数组中的数字用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

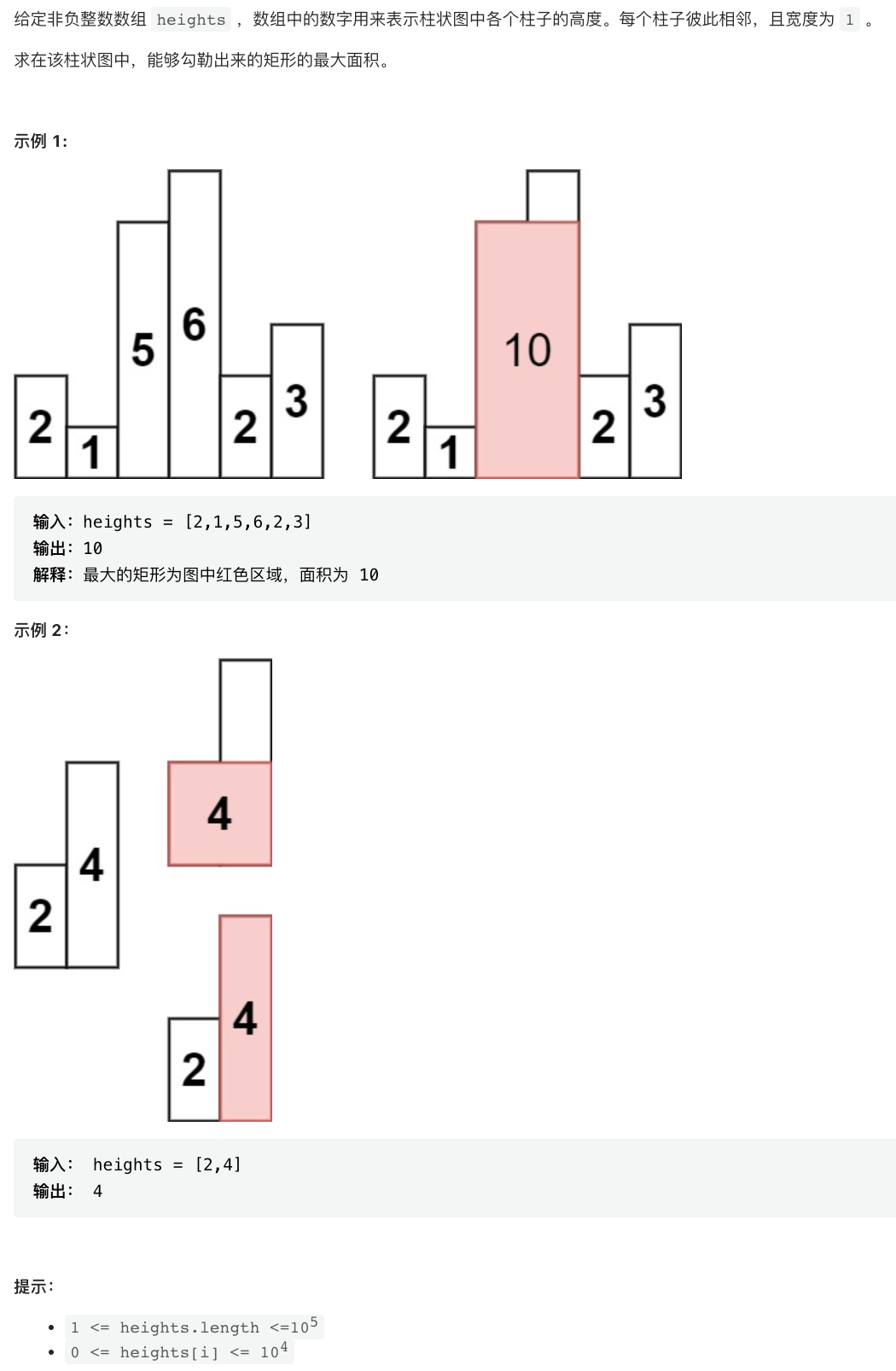
链接：https://leetcode.cn/problems/0ynMMM

思路

还是使用单调栈。你会发现，这几道题的核心，都是利用一个单调栈，之后在遍历数组时，让当前元素和栈顶元素做比较，一直保证栈顶元素是最大（或最小）。

解答这一道题的几个核心点如下：

1. 以一个柱的高度为中心，向两边扩散找边界。找到比这个柱子矮的柱子，就是边界。这时就可以根据柱的高度和边界长度计算面积了。
2. 用一个栈顶大于栈底的单调栈，来维护左边界。
   1. 如果遍历到的当前元素大于栈顶元素，则入栈。
   2. 如果遍历到的当前元素小于栈顶元素，则栈顶元素则为柱，而当前元素的位置，就是最右端的边界。而因为是单调栈，所以栈顶下面的元素，则是栈顶为柱时，最右端的边界。
   3. 将栈顶出栈，比较新的栈顶和当前元素的大小关系，重复前两条的逻辑
3. 遍历完毕，再将栈中还存在的元素，做进一步计算。只有最右边的柱高于前面的柱时，才会出现这种情况。因此此时的右边界，就是数组的右边界。

解法：单调栈

代码

public int largestRectangleArea(int[] heights) {
    Deque<Integer> stack = new ArrayDeque<>();
    // 方便处理边界问题
    stack.push(-1);
    int result = 0;
    for (int i = 0; i < heights.length; i++) {
        int current = heights[i];
        while (stack.peek() != -1 && heights[stack.peek()] > current) {
            // 获取栈顶元素下标的同时移除了栈顶元素
            int height = heights[stack.pop()];
            int with = i - stack.peek() - 1;
            result = Math.max(result, height * with);
        }
        stack.push(i);
    }
    // 处理栈中剩余的边界。此时右边界必然是数组的最右端
    while (stack.peek()!=-1) {
        result = Math.max(result, heights[stack.pop()] * (heights.length - stack.peek() - 1));
    }
    return result;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

提交结果

P.S.这个题解的动画很棒：https://leetcode.cn/problems/0ynMMM/solution/hua-luo-yue-que-wo-zhen-de-zhen-de-nu-li-ohjt/