---

0 前言

本文基于路径规划做一个算法应用，即先构造二维栅格密室，发布密室入口和出口，规划机器人从入口到出口逃生的路线，仿真效果动图如下所示，看完本文相信你也可以做到！

1 什么是路径规划？

通过导航技术对环境进行建模和定位、控制运动、探测障碍物、躲避障碍物，移动机器人可以在导航技术的支持下完成诸多综合性任务，已大规模应用于娱乐、医疗、采矿、救援、教育、军事、太空、农业等领域。

路径规划主要解决移动机器人从某一位置至另一位置的无冲突最优化问题。根据作业环境中障碍物的位置和状态是否随时间变化，路径规划技术可以大致分为

• 静态路径规划
• 动态路径规划

另外，根据机器人在开始移动前还是移动过程中形成路径的规划结果，又可以将路径规划技术分为

• 在线规划
• 离线规划

在线路径规划技术中，移动机器人通过其本身附着的本地传感器获取作业空间信息，根据作业环境变化移动机器人能够及时生成或更新最优化路径。根据机器人的目标位置是否具有移动性，路径规划又可分为

• 静态目标路径规划
• 动态目标路劲规划

各种应用和作业场景均需不同的路径规划算法来实现。

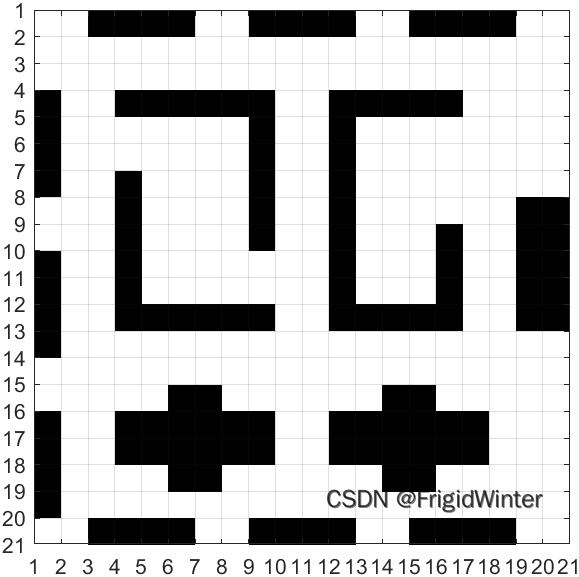
2 栅格建模：构造密室

栅格法主要思路是将区域划分为不重叠的栅格，用连接图从一个栅格格遍历到另一个栅格，遍历没有障碍物的栅格完成从初始位置到目标位置的路径规划。存在障碍物的栅格一分为二，其中不存在障碍的格栅回归到算法中。初始位置和目标位置均通过栅格表示，规划结果由栅格连接生成的路径表示。

本文采用栅格地图对环境建模，生成地图的函数如下：

function map = generateMap(size, obstacle)
%% 
% @breif: 生成栅格地图
% @prama[in]: size -> 生成栅格地图的大小
% @prama[in]: obstacle -> 静态障碍物
% @retval: map -> 栅格地图

%% 栅格数值含义
% 1 ------ 空地
% 2 ------ 静态障碍物
% 3 ------ 任务点
% 4 ------ 智能体

%%
% 初始化全局栅格地图
map = ones(size(1), size(2));
% 初始化静态障碍
map(obstacle) = 2;
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

如何使用该函数呢？请看一个实例：

% 静态障碍物
obs1 = 4:7;
obs2 = [41, 61, 81, 101];
obs3 = 368:372;
obs4 = [64,84, 104, 124, 144, 164, 165, 166, 167, 168, 169];
obs5 = [67, 68, 69, 70, 71, 72, 92, 112, 132, 152, 172];
obs6 = [76, 77, 96, 97, 115, 116, 117, 118, 135, 136, 137, 138, 156, 157, 176, 177];
obs7 = [224, 225, 226, 227, 228, 229, 230, 231, 232, 244, 264, 284, 304, 252, 272, 292, 312, 311, 310, 309];

obstacle = [obs1, obs1 + 6, obs1 + 12, obs2, obs2 + 120, obs2 + 240, obs2 + 19,...
            obs2 + 139, obs2 + 259, obs3, obs3 + 20, obs4, obs5, obs6, obs6 + 160, obs7];

% 初始化地图
map = generateMap([20, 20], obstacle);

% 打印
plotMap(map);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

打印出来就是这样的效果，大家可以根据自己的喜好、实际应用的场景，发挥想象力自行设计“密室”。

3 发布首末位置

用栅格坐标确定首末位置。

start = [20, 1];
goal = [1, 20];
1
2

用不同颜色区分首末位置，并打印到地图上。

function s = plotSquare(pts, size, G, color)
[ptsX, ptsY] = gridN2Xy(pts(:, 1) + size * (pts(:, 2) - 1), size, G);
ptsNum = length(ptsX);
for i=1:ptsNum
    s = scatter(ptsX, ptsY, 270, 'Marker', 'square', 'MarkerEdgeColor', color, ...
             "MarkerFaceColor", color);
end
end
1
2
3
4
5
6
7
8

4 执行路径规划

这里采用最简单的贪婪最佳优先算法。

贪婪最佳优先搜索是一种启发式搜索算法，是广度优先搜索算法的一种改进；算法思想是将节点按距离目标的距离进行排序，然后以这个距离为代价选择待扩展的节点。

• 广度有限搜索算法相当于一个先进先出的队列；
• 深度有限搜索则相当于一个后进先出的栈；
• 贪婪最佳优先搜索则相当于一个根据与终点的距离进行排序的优先级队列。

没有障碍物的情况下，贪婪最佳优先算法通常可以找到一个最短路径而且效率比BFS要高，但在有障碍物的情况下，不一定能找到一个最优路径。

算法逻辑如下：

% 初始化参数
open  = [start, 0, h(start, goal), start]; % Open表
close = [];                      % Closed表
flag  = false;                  % 规划结束标志
next  = [-1, 1, 14;...        % 探索邻域
                0, 1, 10;...
                1, 1, 14;...
              -1, 0, 10;...
                1, 0, 10;...
              -1, -1, 14;...
                0, -1, 10;...
                1, -1, 14];
neighborNum = length(next(:, 1));

while ~flag
    % 【失败】Open表为空仍未找到目标
    if isempty(open(:,1))
        return;
    end
    % 【成功】目标点出现在Open表中
    gIndex = locList(goal, open, [1:2]);
    if gIndex
        close = [open(gIndex, :); close];
        cost = open(gIndex, 3);
        flag = true;
        break;
    end
    
    % 代价评估
    [val, index] = min(open(:, 4));
    curNode = open(index, :);
    close = [curNode; close];   % 最小代价节点入Closed表
    open(index, :) = [];              % 最小代价节点出Open表
    
    % 评估当前节点的邻域扩展节点
    for i=1:neighborNum        
        % 初始化邻域节点
        neighborNode = [curNode(1) + next(i, 1), ...
                        curNode(2) + next(i, 2), ... 
                        curNode(3) + next(i, 3), ...
                        0, curNode(1), curNode(2)
                        ];
        neighborNode(4) = h(neighborNode(1:2), goal);
        
        % 障碍判断
        if map(neighborNode(1), neighborNode(2)) == 2
            continue;
        end
        
        % 更新Open表
        open = updateOpen(neighborNode, open, close);
    end    
end

% 回溯路径
path = backPath(close, start);
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

5 演示测试

在我们构造的这个密室里，选择不同的入口和出口，测试机器人能否规划出密室逃脱的合法路径，这里额外做一个测试案例如下图

效果良好~

---

🔥 更多精彩专栏：

• 《机器人原理与技术》
• 《ROS从入门到精通》
• 《计算机视觉教程》
• 《机器学习》
• 《数值优化方法》
• …

🏠 私信进入AI技术交流群，白嫖30G电子书和教学资源，定期发布AI知识干货、免费科技实体书等福利！

👇配套代码 · 优质体验 · 系统知识 请关注👇