442. 数组中重复的数据

https://leetcode-cn.com/problems/find-all-duplicates-in-an-array/

数组中的元素只会出现1次或2次，如果使用map进行计数的话可以很容易解决，但是题目中还给了另外一个条件：数组中的元素范围是[1,n] 可以利用这个范围 具体的做法：当遍历到某个数num时，将数组num-1位置上面的元素取负值，这样当下次如果出现同样的num,就可以根据nums[num-1]的正负情况得知num是否出现过
注意点：当取当前遍历到的元素时，可能前面的操作已经将当前位置的元素变成负值了，因此取num的时候加一个绝对值

class Solution {
    public List<Integer> findDuplicates(int[] nums) {
         List<Integer> ans=new ArrayList<>();
         int n=nums.length;
         for(int num:nums){
             num=Math.abs(num);
             if(nums[num-1]<0)
                ans.add(num);
             else
                nums[num-1]=-nums[num-1];
         }
         return ans;
    }
}
//O(n)
//O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

453. 最小操作次数使数组元素相等

https://leetcode.cn/problems/minimum-moves-to-equal-array-elements/

思路：从相对的角度考虑，n-1个数的加一操作，相当于1个数的减一操作，那么一个数组中每次进行一个数的减一操作，什么时候数组中的元素都相等呢？答案是当数组中的元素都减小到原始数组中的最小值，所以先找出原始数组中的最小值，统计每个元素和最小值的差值和就是需要操作的次数

class Solution {
    public int minMoves(int[] nums) {
        int min=Arrays.stream(nums).min().getAsInt();
        int ans=0;
        for(int num:nums){
            ans+=(num-min);
        }
        return ans;
    }
}
//O(n)
//O(1)
1
2
3
4
5
6
7
8
9
10
11
12

462. 最少移动次数使数组元素相等 II

https://leetcode.cn/problems/minimum-moves-to-equal-array-elements-ii/

思路：找到数组中的中位数，比中位数小的数进行加一操作，比中位数大的数进行减一操作，直到数组中的元素都等于中位数，这种方式的操作次数最少

class Solution {
    public int minMoves2(int[] nums) {
        Arrays.sort(nums);
        int n=nums.length;
        int mid=n%2==1?nums[n/2]:(nums[(n-1)/2]+nums[n/2])/2;
        int ans=0;
        for(int num:nums){
            ans+=Math.abs(num-mid);
        }
        return ans;
    }
}
//O(nlogn)
//(logn)
1
2
3
4
5
6
7
8
9
10
11
12
13
14

413. 等差数列划分

https://leetcode.cn/problems/arithmetic-slices/

思路：先求出nums[1]-nums[0]的差值d作为初始的公差, 然后往后遍历，i从2k开始，判断nums[i]-nums[i-1]是否的对于d, 如果等于则符合条件的子数组个数加一；否则，就更新当前的公差d, 说明开始了新的公差形成的子数组的遍历过程

class Solution {
    public int numberOfArithmeticSlices(int[] nums) {
        int n=nums.length;
        if(n<3){
            return 0;
        }
        int d=nums[1]-nums[0];
        int ans=0;
        int t=0;
        for(int i=2;i<n;i++){
            if(nums[i]-nums[i-1]==d){//后一个和前一个的差=公差d 数组个数+1
                t++;
            }else{//不等于公差 说明开启一个新的公差的等差数组
                d=nums[i]-nums[i-1];//更新公差
                t=0;
            }
            ans+=t;//累加
        }
        return ans;
    }
}
//O(n)
//O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

697. 数组的度

https://leetcode.cn/problems/degree-of-an-array/

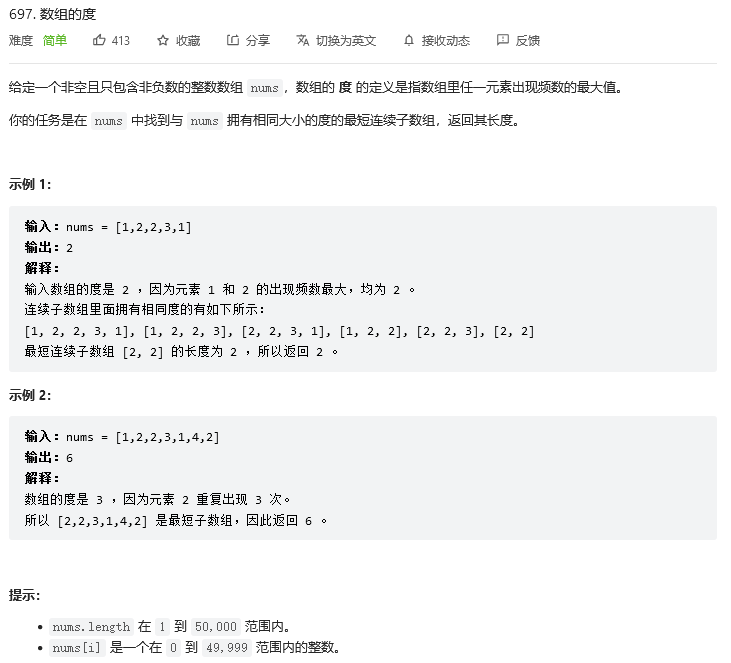
思路：建立一个map, map的key是数组中的数字，value是一个大小为3的数组，第一个位置存放key出现的次数，第二个位置存放key在数组中第一次出现的位置，第三个位置存放key在数组中最后一次出现的位置，然后遍历一遍map找出最大出现次数，然后再遍历一遍map，找出最小间隔

class Solution {
    public int findShortestSubArray(int[] nums) {
        HashMap<Integer,int[]> cnt=new HashMap<>();
        for(int i=0;i<nums.length;i++){
            int num=nums[i];
            if(cnt.containsKey(num)){
               cnt.get(num)[0]++;//次数加一
               cnt.get(num)[2]=i;//跟新后一次出现的位置
            }else{
                cnt.put(num,new int[]{1,i,i});//第一次出现
            }
        }
        int max=0;
        for(int[] value:cnt.values()){
            max=Math.max(max,value[0]);//找到最大出现次数
        }
        int min=Integer.MAX_VALUE;
        for(int[] index:cnt.values()){
            if(index[0]==max){//出现最大次数的数字
                 min=Math.min(min,index[2]-index[1]);//结束位置-开始位置
            }
           
        }
        return min+1;
    }
}
//O(n)
//O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

498. 对角线遍历

https://leetcode.cn/problems/diagonal-traverse/

思路：
上述矩阵有以下规律：

1. 一共有m+n-2条对角线，编号为0-m+n-2, 偶数编号的对角线从左下到右上，奇数编号的对角线从右上到左下
2. 从左下往右上遍历时：如果i(对角线编号)<m, 遍历的开始位置是(i,0); 如果i(对角线编号)>=m, 遍历的开始位置是(m-1,i-m+1);
3. 从右上往左下遍历时：如果i(对角线编号)<n, 遍历的开始位置是(0,i); 如果i(对角线编号)>=n, 遍历的开始位置是(i-n+1,n-1);

class Solution {
    public int[] findDiagonalOrder(int[][] mat) {
        int m=mat.length,n=mat[0].length;
        int[] ans=new int[m*n];
        int index=0;
        for(int i=0;i<=m+n-2;i++){//一共m+n-2条对角线  编号0-m+n-2
            if(i%2==0){//从从左下到右上
                int x=i<m?i:m-1;
                int y=i<m?0:i-m+1;
                while(x>=0&&y<n){
                    ans[index++]=mat[x][y];
                    x--;
                    y++;
                }
            }else{//右上到左下
                int x=i<n?0:i-n+1;
                int y=i<n?i:n-1;
                while(x<m&&y>=0){
                    ans[index++]=mat[x][y];
                    x++;
                    y--;
                }
            }
        }
        return ans;
    }
}
//O(m*n)
//O(1) 保存答案的数组不计空间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

525. 连续数组

https://leetcode.cn/problems/contiguous-array/

思路：使用一个计数器，当遇到0时减一，遇到1时加一，同时使用一个map记录计数器的值和对应的遍历到的数组的下标，当遍历数组遇到某个计数值之前已经出现过了，此时更新连续数组长度，两次的出现位置之间的数据中的0和1的个数相同

class Solution {
    public int findMaxLength(int[] nums) {
        HashMap<Integer,Integer> map=new HashMap<>();
        map.put(0,-1);//初始化放入0 -1  比如数组在只有[0,1]两个元素时 第一次出现计数和为0的位置为-1 第2次是1 
        //1-(-1)=2 保证了边界条件的正确性
        int cur=0;
        int ans=0;
        for(int i=0;i<nums.length;i++){
            if(nums[i]==0){//遇到0计数减一(改成遇0加一也可)
                --cur;
            }else{//遇到1计数加一(改成遇1减一也可)
                ++cur;
            }
            if(map.containsKey(cur)){//之前cur的次数出现过 假设上一次位置是index 这次位置是i
            //num[index+1,i]区间内的0 1个数相同
                ans=Math.max(ans,i-map.get(cur));
            }else{
                map.put(cur,i);//更新出现位置
            }
        }
        return ans;
    }
}
//O(n)
//O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

532. 数组中的 k-diff 数对

思路1：排序+二分查找，排完序后遍历0-n-2位置的元素，对每个元素num查找num+k, 如果num+k在数组中存在，则说明存在k-diff对(num,num+k), 注意重复的元素处理，当存在1 1 1 这种连续的情况时，我们只处理第一个1

class Solution {
    public int findPairs(int[] nums, int k) {
       Arrays.sort(nums);
       int left=0,right=nums.length-1;
       int ans=0;
       for(int i=0;i<nums.length-1;i++){
           if(i==0){
               if(binarySearch(nums,i+1,nums.length-1,nums[i]+k)!=-1){
                   ans++;
               }
           }else if(i>0&&nums[i]!=nums[i-1]){//去重
                if(binarySearch(nums,i+1,nums.length-1,nums[i]+k)!=-1){
                   ans++;
               }
           }
          
       }
       return ans;
    }
    public int binarySearch(int[] nums,int left,int right,int target){
        while(left<=right){
            int mid=left+(right-left)/2;
            if(nums[mid]==target){
                return mid;
            }else if(nums[mid]>target){
                right=mid-1;
            }else if(nums[mid]<target){
               left=mid+1;
            }
        }
        return -1;
    }
}
//O(nlogn) 排序: nlogn  二分：logn+log(n-1)+log(n-2)+...+log(1)
//O(logn)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

思路2：使用两个set, 一个标记已经访问过的元素，另外一个set保存元组(x,y)中的左边的元素，最终的保存x的set的大小就是符合条件的元组的个数

class Solution {
    public int findPairs(int[] nums, int k) {
       HashSet<Integer> vis=new HashSet<>();
       HashSet<Integer> ans=new HashSet<>();//只放数对(x,y)中的x
       for(int num:nums){
           if(vis.contains(num-k)){//当前遍历到的元素是num 并且num-k已经出现过
               ans.add(num-k);//(num-k,num)
           }
           if(vis.contains(num+k)){//当前遍历到的元素是num 并且num+k已经出现过
               ans.add(num);//(num,num+k)
           }
           vis.add(num);
       }
       return ans.size();
    }
    
}
//O(n)
//O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

1089. 复写零

https://leetcode.cn/problems/duplicate-zeros/

思路1：暴力法，每遇到1个0就将该0后面的元素往后移动一个位置，重复这个过程，知道遍历结束

class Solution {
    public void duplicateZeros(int[] arr) {
        int n=arr.length;
        for(int i=0;i<n;i++){
            if(arr[i]==0){//每遇到一个0就将后面的元素往后移动
                int j=n-1;
                while(j>i+1){
                    arr[j]=arr[j-1];
                    j--;
                }
                if(i+1<n)
                    arr[i+1]=0;
                i++;    
            }
        }
    }
}
//O(n^2)
//O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

思路2：两次遍历，第一次遍历计算出0的个数，对于某个位置i上面的元素而言，它最终的位置是i+cnt0, 即nums[i]左边有几个0，它就需要往右移动几次，所以知道nums[i]左边有几个0，就可以知道nums[i]最终的位置

class Solution {
    public void duplicateZeros(int[] arr) {
        int n=arr.length;
        int cnt0=0;
        for(int i=0;i<n;i++){
            if(arr[i]==0){
                cnt0++;//统计0的个数
            }
        }
        for(int i=n-1;i>=0;i--){
            if(arr[i]==0){//从后往前遍历 遇到一个0 说明某个位置左边的0的个数减少
                cnt0--;
            }
            if(i+cnt0<n){
                arr[i+cnt0]=arr[i];//arr[i]向右移动cnt0个位置
                if(arr[i]==0&&i+cnt0+1<n){//arr[i]是0的话 还需要补上一个0 原始的0移动+复制1个0
                    arr[i+cnt0+1]=0;
                }
            }
        }
    }
}
//O(n)
//O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

888. 公平的糖果交换

https://leetcode.cn/problems/fair-candy-swap/

思路：假设alice的糖果数目是sum1,bob的糖果数目是sum2, alice交换出的糖果数是x, bob交换出的糖果数是y,则有

$sum1-x+y=sum2-y+x==>x=\frac{sum1-sum2}{2}+y$

因此可以使用一个set记录alice拥有的每盒的糖果数x，对于bob拥有的每盒的糖果数y， 根据y计算出x，判断x是否出现在集合set中即可

class Solution {
    public int[] fairCandySwap(int[] aliceSizes, int[] bobSizes) {
        int sum1=Arrays.stream(aliceSizes).sum();
        int sum2=Arrays.stream(bobSizes).sum();
        HashSet<Integer> set=new HashSet<>();
        for(int ele:aliceSizes){
            set.add(ele);
        }
        int delta=(sum1-sum2)/2;
        int[] ans=new int[2];
        for(int y:bobSizes){
            if(set.contains(y+delta)){
                ans[0]=y+delta;
                ans[1]=y;
                break;
            }
        }
        return ans;
    }
}
//O(n+m)
//O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22