-
CVPR 2022 Best Paper -- Learning to Solve Hard Minimal Problems
Learning to Solve Hard Minimal Problems*
CODE: petrhruby97/learning_minimal
Minimal problem —— 附一个非常好的BLOG-Jin’s Blog
###[该博客解答了来自初学者的很多疑惑点]
###[这里解释了为什么神经网络能够学到这个问题 ==> problem-solution pair中problem对应的solution在大部分情况下都是连续的]
基于不同的假设,问题会有不同的自由度,当我们使用最少的输入点来解决问题时,那么这就是一个 Minimal problem,一般翻译为「最小配置问题」。

Abstract
-
Hard Minimal Problems 来源于 原始几何优化 <=> 具有许多伪解的极小问题
-
本文方法避免大量计算伪解
-
本文设计了一个学习策略来选择 对于问题和可能的解都是数值连续的 初始problem-solution pair
-
本文开发了一个RANSAC求解器 通过每个视图四点的最小松弛 来求解三个已校准相机的相对位姿 【Hard Minimal Problems】
Introduction
minimal problems 用于求解 取决于输入数据并且具有有限解的多项式方程组系统。
Motivation
许多几何问题 只有一个最优解。然而,Minimal Problems往往会产生许多额外的伪解。最优解通常是真实的,满足不等式约束,并能很好地适合所有数据。然而,这样的约束不能被非线性代数方法所使用,这些方法必须寻找多项式系统的所有解。
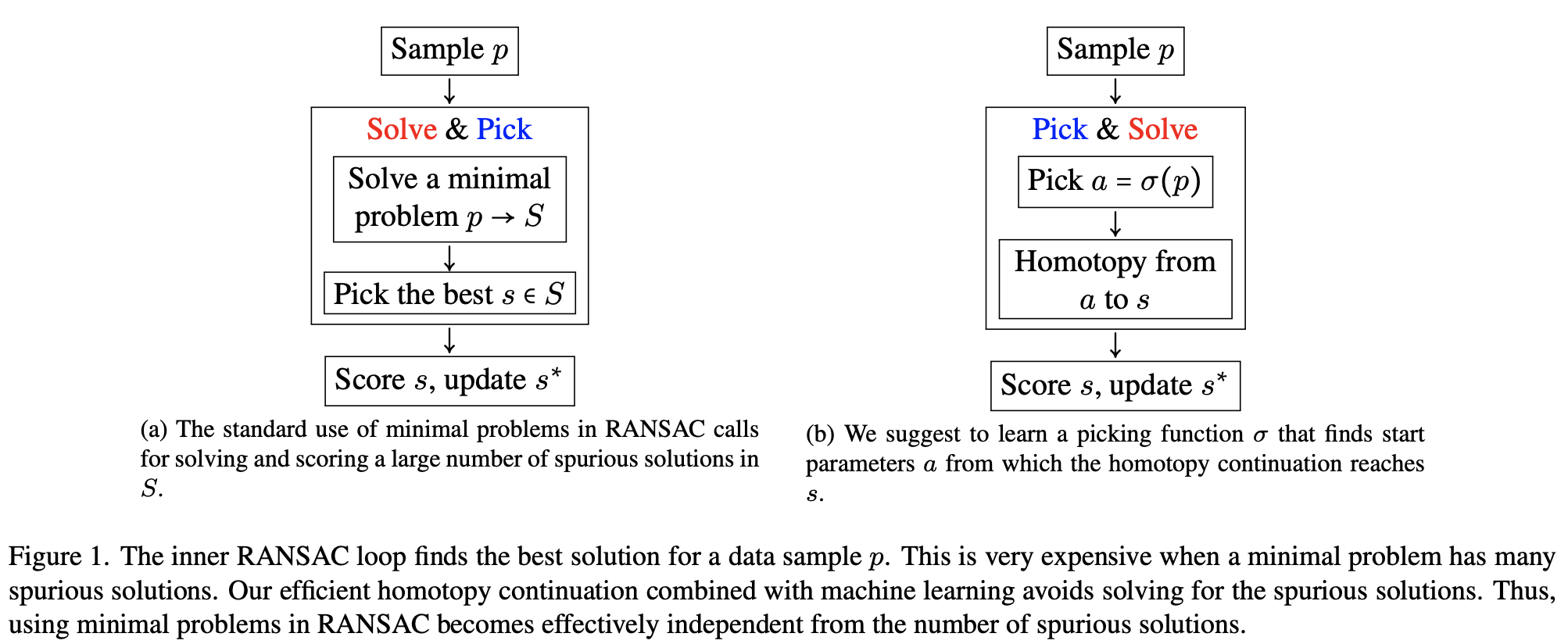
RANSAC通过从数据样本中 计算候选解 并挑选出具有最多数据支持的解 来逼近几何问题的最优解。这是通过在外循环中对 样本 进行迭代,在内循环中对每个样本的minimal problem的解 进行迭代来实现的。为了在内循环中为数据样本找到一个唯一的解,最先进的 "解决与挑选 "方法 首先计算一个minimal problem的所有解,然后通过去除 非真实解、使用不等式、评估支持度来选择最优解。当minimal problem有许多伪解时,内循环中的优化可能是非常昂贵的。图1 比较了标准的 "解决和挑选 "方法和我们的 "挑选和解决 "方法,对于一个给定的数据样本,本文方法会学习如何首先挑选一个有希望的起点,然后继续寻找一个有意义的解。
Contribution
本文所提出的方法将 optimized Homotopy Continuation (HC) 和机器学习结合起来避免求一些伪解。其主要思想是通过为一个真实的HC路径学习一个单一的起始点使得它对于原始的几何问题能够有更大可能性求得好的解。
本文选择了 使用 松弛四点估计三个相机相对位姿的超约束问题 作为有效解决Hard Minimal Problems的验证。
对于 4pt problem, 求解 26.3% 输入大约耗时 16.3µs,在RANSAC中求解时间平均为61.6µs。对于 5pt problem, 求解 29.0% 输入大约耗时7.6µs,在RANSAC中求解时间平均为26.1µs。本文方法在速度上非常高效,也是通用的。
Conclusion
本文方法使用有效的 Homotopy Continuation 和 Machine Learning 解决了RANSAC框架中的困难最小配置问题,快速且正确。
Limitations
- 牺牲了 复杂HC method 的高成功率 以换取 更容易失败但更快速、实时的HC method。但是,当与训练好的模型相结合后,成功频率足以在RANSAC中发挥作用。
- MLP模型只表示它所被训练的内容。但它还是能够代表真实的数据分布,同时保持少量、快速评估。拟合特定数据分布 对于某些特殊场景或许是有用的。(eg. 摄像机被安装在车辆上,具有特殊的运动)
-
-
相关阅读:
LeetCode 每日一题——1302. 层数最深叶子节点的和
Golang开发--计时器(Timer)和定时器(Ticker)
c++中的string类
php+mysql实现补齐24小时时间段同时赋值0的后端解决方案
批量快捷创建新数组的几种方式
技术人创业:失败不是成功,但反思是
前端面试题: js中对比两个对象的值是否相等? for..in 和 for...of的区别?
一文读懂css【css3】绝对(absolute)定位和相对(relative)定位 相对定位是相对谁定位的 绝对定位又是根据谁绝对定位的 子绝父相 包含块
做网站有哪些注意事项
js中的this关键字
- 原文地址:https://blog.csdn.net/Nismilesucc/article/details/125959970