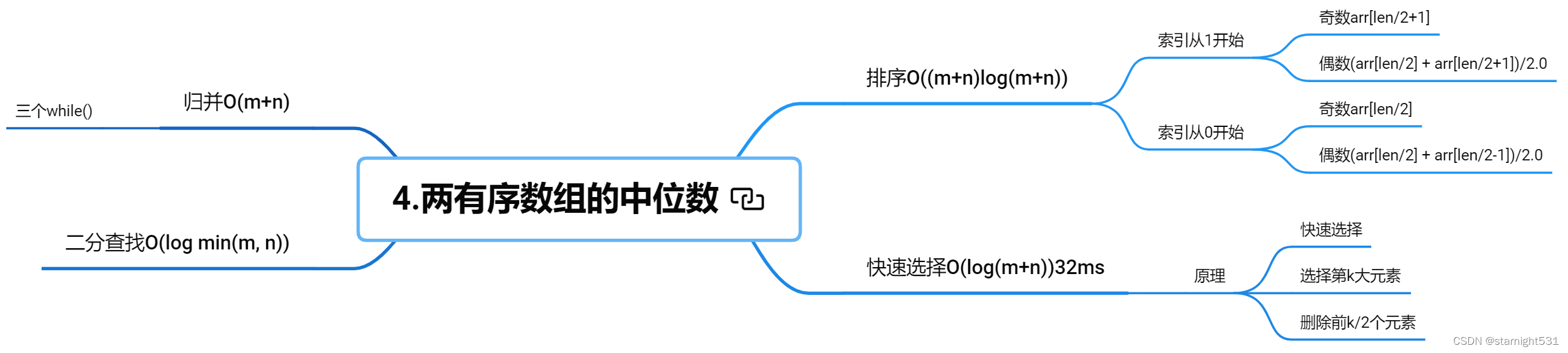
Leetcode4.寻找两个正序数组的中位数 - 1/2+2种方法

食用指南：

Leetcode专栏开启了，由于博主闭关期末，所以每日只能一题
尽量做到一题多解，先说思路，之后代码实现，会添加必要注释
语法或STL内容会在注意点中点出，新手友好
欢迎关注博主神机百炼专栏，内涵算法基础详细讲解和代码模板

题目描述：

• 给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

  算法的时间复杂度应该为 O(log (m+n)) 。

• 代码背景

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {

    }
};
1
2
3
4
5
6

• 题目来源：https://leetcode.cn/problems/median-of-two-sorted-arrays/

题目分析：

• 法一：快速选择

  对于长为n的有序数组来说，中位数就是第n/2 或 (n+1)/2大的数

  现将有序数组中前m个数据扔掉，且保证没有扔掉中位数

  则剩余长n - m的数组中第 n/2 - m 或 (n+1)/2 - m大的数就是原数组的中位数

• 法二：二分查找

  太难了，属实不会，属实是🐀

算法模板:

• 快速选择
• 归并排序

代码实现：

法一：快速选择

• 从1计数寻找中位数版本：

#include <algorithm>
class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int len = nums1.size() + nums2.size();
        if (len % 2 == 0){
            int l = findkthnum(0, nums1, 0, nums2, len/2);  //举例：0 1 2 3 则中位数是第4/2 = 2个 和 第3个
            int r = findkthnum(0, nums1, 0, nums2, len/2+1);
            return (l+r)/2.0;
        }
        return findkthnum(0, nums1, 0, nums2, len/2+1);   //举例：0 1 2 则中位数是3/2 = 1，第 1 + 1 个
    }
    int findkthnum(int s1, vector<int> &nums1, int s2, vector<int> &nums2, int k){  //此处的第k个数是从1开始计数的，但是s12从0开始
        if (s1 == nums1.size())   return nums2[s2+k-1];
        if (s2 == nums2.size())   return nums1[s1+k-1];

        if (k == 1){
            return min(nums1[s1], nums2[s2]);
        }

        int i = min(s1 + k/2, (int)nums1.size()), j = min(s2 + k - k/2, (int)nums2.size());
        if (nums1[i-1] < nums2[j-1])    return findkthnum(i, nums1, s2, nums2, k-i+s1);    
        return findkthnum(s1, nums1, j, nums2, k-j+s2);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

• 目标寻找第k = (m+n)/2个元素，每次删除前k/2个元素
  当删除logk次，则最终剩余的1个元素就是中位数

法二：二分查找：

• 不会

O(n+m)：归并

• 获得两个分别有序的的数列是合成最终有序序列的倒数前一步
• 只需要归并排序的归并过程即可

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
    	int len1 = nums1.size(), len2 = nums2.size();
		vector<int> nums;
		int i = 0, j = 0;
		while(i < len1 && j < len2){
			if (nums1[i]<nums2[j])	nums.push_back(nums1[i++]);
			else nums.push_back(nums2[j++])
		}
		while(i < len1) nums.push_back(nums1[i++]);
		while(j < len2) nums.push_back(nums2[j++]);
		if ((len1 + len2)%2) return nums[(len1+len2)/2];
		else return (nums[(len1+len2)/2] + nums[(len1+len2)/2-1])/2.0;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

O((n+m)log(n+m))：排序

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
		vector<int> nums;
		for(auto &iter : nums1){
			nums.push_back(iter);
		}
		for(auto &iter : nums2){
			nums.push_back(iter);
		}
		sort(nums.begin(), nums.end());
		int len = nums.size()
		if (len % 2){
			return nums[len/2];
		}return (nums[len/2] + nums[len/2-1])/2.0;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

注意点：

• vector<int>的size()方法返回值：
  vector<>.size()
  string.size() / string.length()
  三者返回值都是unsigned int

  unsigned int 和 int 做 > < 比较时，
  会将有符号数当作无符号数看，导致比较结果失真
  但是当比较==时，会直接比较补码是否相等
  

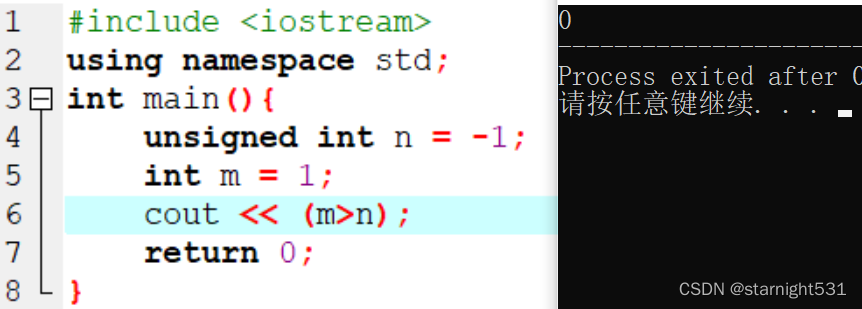
  所以在调用algorithm的min() max()方法时，需要对三者进行强制转型

• 递归写作时，同时存在数组越界 和 递归栈溢出 时

  先避免数组越界，再避免栈溢出