代码随想录（番外）图论1

代码随想录（番外）图论1

1. 深度优先搜索理论基础
2. 所有可能的路径
3. 广度优先搜索理论基础.md

https://programmercarl.com/%E5%9B%BE%E8%AE%BA%E6%B7%B1%E6%90%9C%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html

1. 深度优先搜索理论基础
总结
同理回溯算法，换汤不换药
二叉树递归讲解 (opens new window)中，给出了递归三部曲。
回溯算法 (opens new window)讲解中，给出了 回溯三部曲。

其实深搜也是一样的，深搜三部曲如下：

1.确认递归函数，参数
2.确认终止条件
3.处理目前搜索节点出发的路径

2. 所有可能的路径

class Solution {
public:
    vector<vector<int>> result;//存符合条件结果路径
    vector<int> path;//0结点到终点路径
    //x:目前遍历的结点
    //graph：存当前的图
    void dfs (vector<vector<int>>& graph,int x)
    {
                // 要求从节点 0 到节点 n-1 的路径并输出，所以是 graph.size() - 1
        if(x==graph.size()-1) // 找到符合条件的一条路径
        {
            result.push_back(path);
            return ;
        }

        for(int i=0;i<graph[x].size();i++)// 遍历节点n链接的所有节点
        {
            path.push_back(graph[x][i]);// 遍历到的节点加入到路径中来
            dfs(graph,graph[x][i]);// 进入下一层递归
            path.pop_back();// 回溯，撤销本节点
        }

    }

    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        path.push_back(0); // 无论什么路径已经是从0节点出发
        dfs(graph,0); // 开始遍历
        return result;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

同理回溯也就是，像树一样同过深度一层一层找出路径。

3. 广度优先搜索理论基础.md

具体作用就是同过一圈一圈的方式把最短路径找出。
上面我们提过，BFS是一圈一圈的搜索过程，但具体是怎么一圈一圈来搜呢。

我们用一个方格地图，假如每次搜索的方向为 上下左右（不包含斜上方），那么给出一个start起始位置，那么BFS就是从四个方向走出第一步。

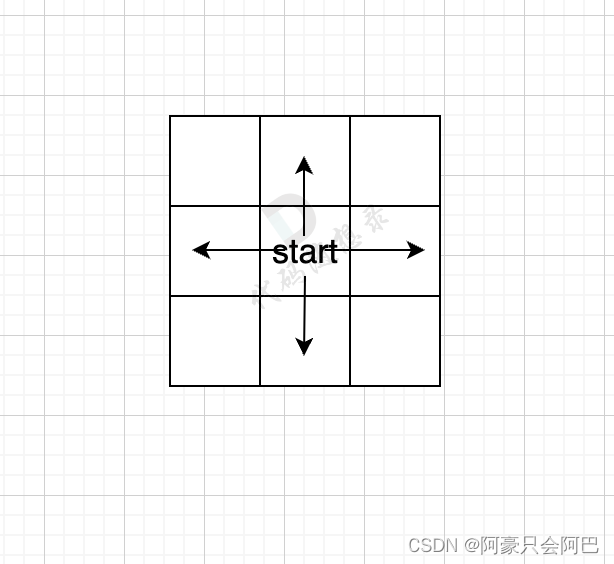
如果加上一个end终止位置，那么使用BFS的搜索过程如图所示：

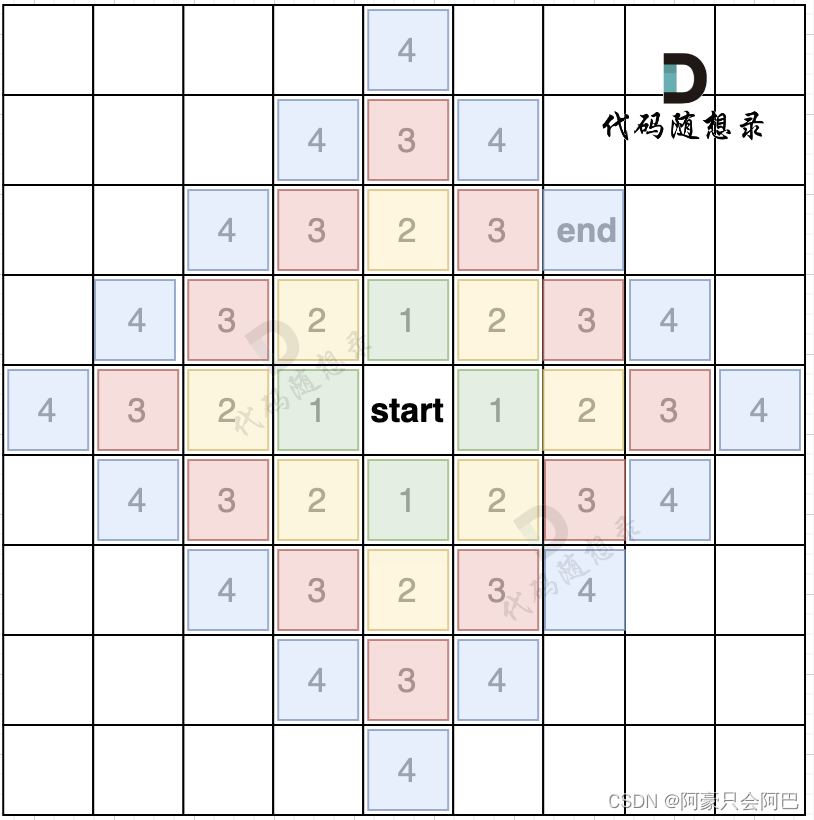
我们从图中可以看出，从start起点开始，是一圈一圈，向外搜索，方格编号1为第一步遍历的节点，方格编号2为第二步遍历的节点，第四步的时候我们找到终止点end。

正是因为BFS一圈一圈的遍历方式，所以一旦遇到终止点，那么一定是一条最短路径。

而且地图还可以有障碍，如图所示：

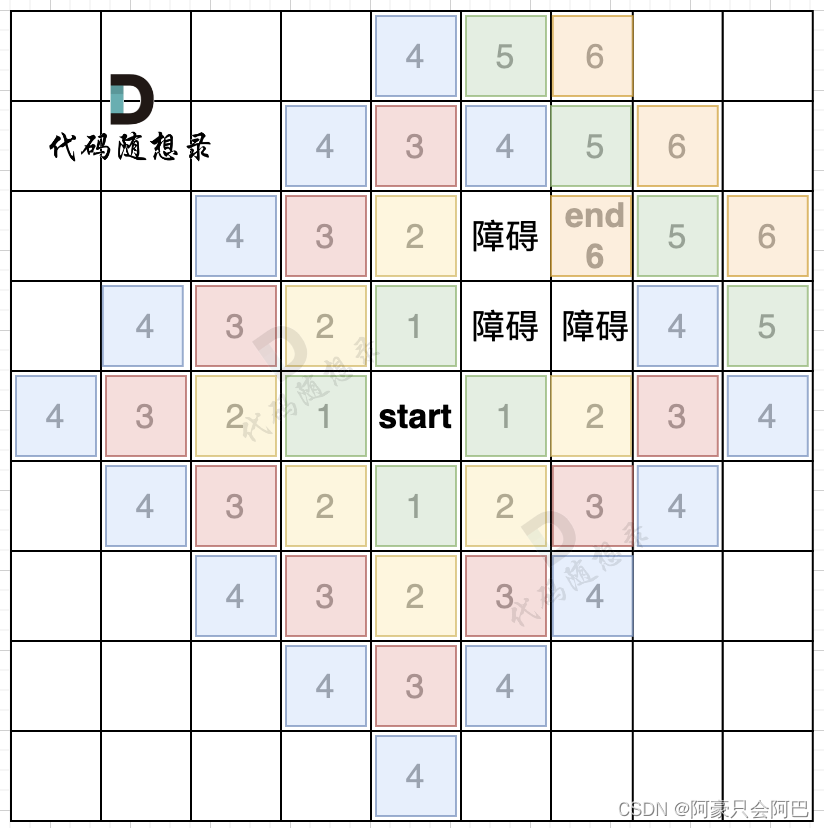
在第五步，第六步 我只把关键的节点染色了，其他方向周边没有去染色，大家只要关注关键地方染色的逻辑就可以。

从图中可以看出，如果添加了障碍，我们是第六步才能走到end终点。

只要BFS只要搜到终点一定是一条最短路径，大家可以参考上面的图，自己再去模拟一下。

看图就可以深入浅出的理解广度优先搜索。

所以用队列，还是用栈都是可以的，但大家都习惯用队列了，所以下面的讲解用我也用队列来讲，只不过要给大家说清楚，并不是非要用队列，用栈也可以。

下面给出广搜代码模板，该模板针对的就是，上面的四方格的地图： （详细注释）

int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 表示四个方向
// grid 是地图，也就是一个二维数组
// visited标记访问过的节点，不要重复访问
// x,y 表示开始搜索节点的下标
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
    queue<pair<int, int>> que; // 定义队列
    que.push({x, y}); // 起始节点加入队列
    visited[x][y] = true; // 只要加入队列，立刻标记为访问过的节点
    while(!que.empty()) { // 开始遍历队列里的元素
        pair<int ,int> cur = que.front(); que.pop(); // 从队列取元素
        int curx = cur.first;
        int cury = cur.second; // 当前节点坐标
        for (int i = 0; i < 4; i++) { // 开始想当前节点的四个方向左右上下去遍历
            int nextx = curx + dir[i][0];
            int nexty = cury + dir[i][1]; // 获取周边四个方向的坐标
            if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 坐标越界了，直接跳过
            if (!visited[nextx][nexty]) { // 如果节点没被访问过
                que.push({nextx, nexty});  // 队列添加该节点为下一轮要遍历的节点
                visited[nextx][nexty] = true; // 只要加入队列立刻标记，避免重复访问
            }
        }
    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

可以直接拿来做 200.岛屿数量 (opens new window)这道题目，唯一区别是 针对地图 grid 中有数字1的地方去做一个遍历。