-
ZKP6.1 Discrete-log-based Polynomial Commitments (Preliminary)
ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 6: Discrete-log-based Polynomial Commitments (Yupeng Zhang)
- Recall
- How to build an efficient SNARK?
- A polynomial commitment scheme + A polynomial interactive oracle proof (IOP) = SNARK for general circuits
- Plonk
- Univariate polynomial commitment + Plonk Polynomial IOP = SNARK for general circuits
- Interactive proofs
- Multivariate polynomial commitment + Sumcheck protocol = SNARK for general circuits
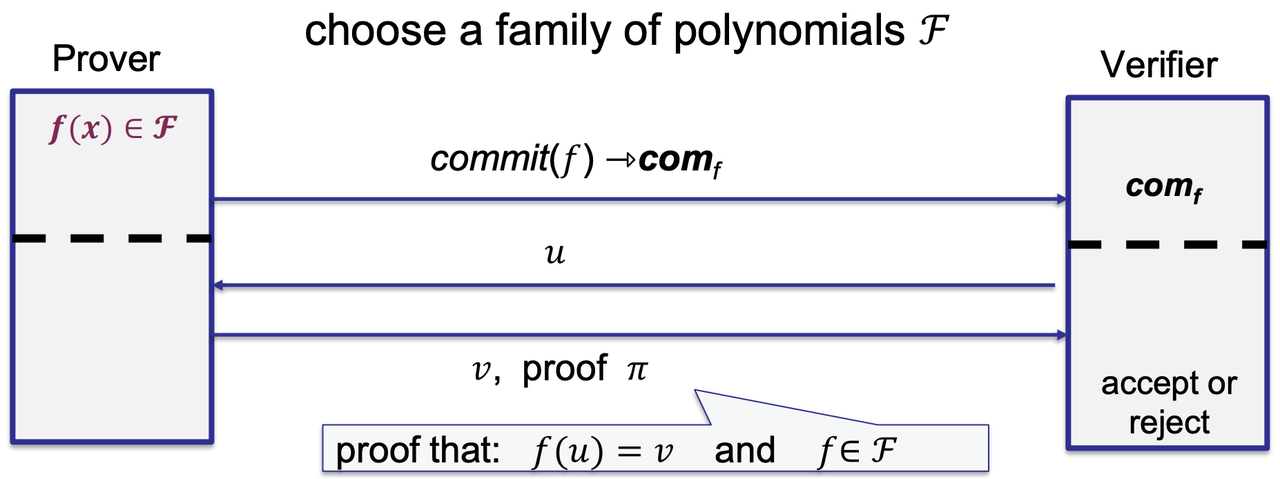
- polynomial commitment
- How to build an efficient SNARK?

6.1 Background
- Group: Closure, Associativity, Identity, Inverse.
- Generator of a group: An element g g g that generates all elements in the group by taking all powers of g g g
- Discrete logarithm assumption
- A group G G G has an alternative representation as the powers of the generator g g g: { g , g 2 , g 3 , . . . , g p − 1 } \{g, g^2, g^3,...,g^{p-1}\} {g,g2,g3,...,gp−1}
- Discrete logarithm problem: given y ∈ G y \in G y∈G, find x x x s.t. g x = y g^x = y gx=y
- Discrete-log assumption: discrete-log problem is computationally hard.
- (Computational) Diffie-Hellman assumption: Given G , g , g x , g y G, g, g^x, g^y G,g,gx,gy, cannot compute g x y g^{xy} gxy
- Bilinear pairing:
- ( p , G , g , G T , e ) (p, G, g, G_T, e) (p,G,g,GT,e)
- G G G and G T G_T GT are both multiplicative cyclic groups of order p p p, g g g is the generator of G G G.
- G G G: base group, G T G_T GT target group
- Pairing:
e
(
P
x
,
Q
y
)
=
e
(
P
,
Q
)
x
y
e(P^x,Q^y) = e(P,Q)^{xy}
e(Px,Qy)=e(P,Q)xy
- Example: e ( g x , g y ) = e ( g , g ) x y = e ( g x y , g ) e(g^x,g^y) = e(g,g)^{xy} = e(g^{xy},g) e(gx,gy)=e(g,g)xy=e(gxy,g)
- Given g x g^x gx and g y g^y gy , a pairing can check that some element h = g x y h = g^{xy} h=gxy without knowing x x x and y y y.
- BLS signature [Boneh–Lynn–Shacham’2001]

- Recall
-
相关阅读:
艾思AI-admin框架开发指导意见与规范1.0
计算机竞赛 机器视觉人体跌倒检测系统 - opencv python
机器学习中的“泛化”:模型过拟合与欠拟合,到底怎么回事?
抖音API:item_search_keyword-抖音关键词月搜查询
C++前缀和算法的应用:统计得分小于K的子数组数目
10.23
在 Arweave 中轻松管理文件:借助 4EVERLAND 完成 Web3 前端Path Manifests的终极指南
【51单片机实验笔记】中断篇(一) 外部中断
Web前端:为移动应用选择Angular框架的3个商业优势!
深度解密 | 灵脉SAST 3.0最新特性曝光
- 原文地址:https://blog.csdn.net/weixin_45347752/article/details/133988092