LeetCode //C - 149. Max Points on a Line

149. Max Points on a Line

Given an array of points where points[i] = [xi, yi] represents a point on the X-Y plane, return the maximum number of points that lie on the same straight line.
 

Example 1:

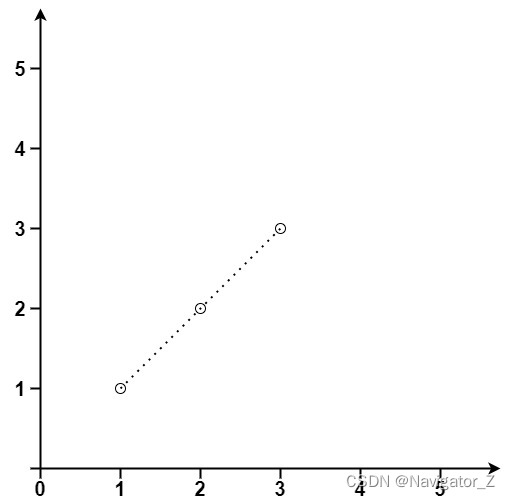
Input: points = [[1,1],[2,2],[3,3]]
Output: 3

Example 2:

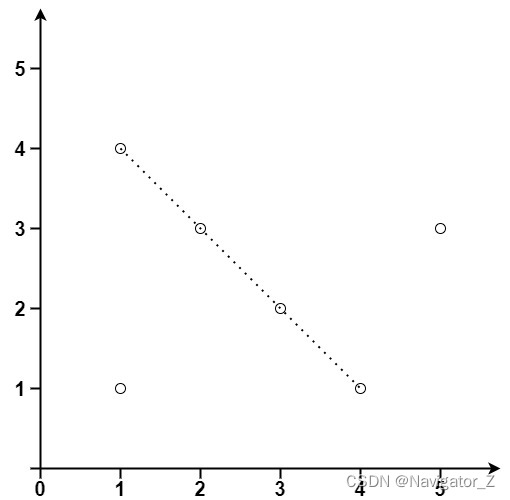
Input: points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
Output: 4

Constraints:

-1 <= points.length <= 300

• points[i].length == 2
• $-10^4<=xi,yi<=10^4$
• All the points are unique.

From: LeetCode
Link: 149. Max Points on a Line

---

Solution:

Ideas：

1. Iterate Over Pairs of Points: The outer two loops iterate through all possible pairs of points. Each pair of points (i, j) defines a potential line.

2. Calculate the Greatest Common Divisor (GCD): For each pair, it calculates the differences in x (dx) and y (dy) coordinates. It then simplifies these differences by dividing them by their greatest common divisor (GCD). This step is crucial because it normalizes the slope of the line. For instance, a slope of 2/4 is the same as 1/2 after reduction by the GCD.

3. Check Other Points: The innermost loop checks all other points to see if they lie on the line defined by the current pair of points. It does this by using the slope-intercept form of the equation of a line. If another point (k), when inserted into the equation formed by points (i) and (j), satisfies the equation, it means that point (k) is also on the same line.

4. Count Points on the Same Line: Each time it finds a point that lies on the line, it increments a counter (lineCount). After checking all points, if lineCount is greater than maxPoints, it updates maxPoints.

5. Return the Maximum: After all pairs have been checked, the function returns the highest value of lineCount, which is the maximum number of points on the same line.

Code:

int gcd(int a, int b) {
    return (b == 0) ? a : gcd(b, a % b);
}

int maxPoints(int** points, int pointsSize, int* pointsColSize) {
    if (pointsSize < 3) {
        return pointsSize;
    }
    
    int maxPoints = 2;
    for (int i = 0; i < pointsSize; ++i) {
        for (int j = i + 1; j < pointsSize; ++j) {
            int lineCount = 2;
            int dx = points[j][0] - points[i][0];
            int dy = points[j][1] - points[i][1];
            int d = gcd(dx, dy);
            dx /= d; // Reduce the difference to its simplest form
            dy /= d; // Reduce the difference to its simplest form
            for (int k = 0; k < pointsSize; ++k) {
                if (k != i && k != j) {
                    if (dx * (points[k][1] - points[i][1]) == dy * (points[k][0] - points[i][0])) {
                        lineCount++;
                    }
                }
            }
            maxPoints = (lineCount > maxPoints) ? lineCount : maxPoints;
        }
    }
    
    return maxPoints;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31