11.16堆的一些性质与操作

 

 

1016 

7，5，4，3，2，6，1

7，4，6，1，3，2，5

没有度为1的结点说明为满树

A.哈夫曼树一定没有度为1的结点。最大堆可能有度为1的结点

D.哈夫曼树可能是完全二叉树

完全二叉树就是结点自左向右排满，即最适合用顺序存储。满二叉树不一定是完全二叉树，因为可以右子树比左子树多一层。完全二叉树也不一定是满二叉树，因为可以只有左孩子。

堆的性质与操作

堆总是满足下列性质：

• 堆中某个结点的值总是不大于或不小于其父结点的值；

• 堆总是一棵完全二叉树。 

堆的插入

堆的插入，就是在堆的最后面去添加一个元素，添加完成之后，就要去进行向上调整操作，

先在队尾插入，然后进行向上调整

//堆的插入
void Heap_Insert(Heap* hp, DataType x) {
	assert(hp);
	//如果此时的堆空间满了，那么就要去扩容空间
	if (hp->size == hp->capacity) {
		DataType* temp = (DataType*)realloc(hp->data,sizeof(DataType)  * (hp->capacity+1));//追加1个空间
		if (!temp) {
			printf("ERROR\n");
			exit(-1);
		}
		hp->data = temp;
		hp->data[hp->size] = x;
		hp->size++;
		hp->capacity++;
	}
	else
	{
		hp->data[hp->size] = x;
		hp->size++;
	}
	Adjust_Up(hp->data, hp->size - 1, hp->size);//插入后进行向上调整
}

堆的删除 

 

//堆的删除,删除根节点
void Heap_Del(Heap* hp) {
	assert(hp);
	if (!isEmpty(hp)) {
		swap(&hp->data[hp->size - 1], &hp->data[0]);//根节点和尾节点进行交换
		hp->size--;
		Adjust_Down(hp->data, 0, hp->size);//向下调整
	}
}

堆的遍历就直接按照数组的顺序去遍历就行了，完全二叉树的逻辑上是从上到下，从左到右去遍历的。

创建堆 

//创建堆
void Heap_Create(Heap* hp, DataType* data, int n) {
	assert(hp);
	hp->data = (DataType*)malloc(sizeof(DataType) * n);
	if (!hp->data) {
		printf("ERROR\n");
		exit(-1);
	}
	for (int i = 0; i < n; i++) {
		hp->data[i] = data[i];//赋值
	}
	hp->size = n;
	hp->capacity = Maxsize;
	for (int j = (n - 1) / 2; j >= 0; j--) {
		//创建完成了之后，就要进行向下调整
		Adjust_Down(hp->data, j ,hp->size);
	}
}

哈夫曼树

哈夫曼树：带权路径长度最小的二叉树。

哈夫曼树的构造：

1. 在给定权值大小的节点序列中选出两个最小权值节点，将算出两节点之和放入序列中。
2. 依次类推每次选出的节点都是2个，所以度均为2.

哈夫曼树不一定是完全二叉树。哈夫曼树是带权路径长度达到最小的二叉树，也叫做最优二叉树，不一定是完全二叉树，也不一定是平衡二叉树。哈夫曼树也可以是k叉的，只是在构造k叉哈夫曼树时需要先进行一些调整。

哈弗曼树可以不唯一，但是他们具有相同的带权路径长度，另外，哈弗曼编码才是唯一的。

哈夫曼树不唯一，因为没有限定左右子树，并且有权值重复时，可能树的高度都不唯一，唯一的只是带权路径长度之和最小。

哈夫曼树（Huffman Tree）是一种特殊的二叉树，它并不一定是完全二叉树。
在哈夫曼编码中，我们要构建一棵二叉树，使得树中每个叶子节点都代表一个字符，而每个非叶子节点的左子树和右子树的权值之和相等，且等于该非叶子节点的权值。这样的二叉树结构可以是不完全的，也就是说，哈夫曼树可以是部分填充的。
然而，当我们构建哈夫曼树时，通常会使用一个优先队列（如最小堆）来保存尚未合并的节点。在每次合并时，我们选择优先队列中权值最小的两个节点进行合并，并将合并后的新节点重新插入优先队列。这个过程会导致哈夫曼树在深度上尽可能平衡，即在每个深度上，左侧和右侧的节点数大致相等。因此，最终的哈夫曼树往往非常接近完全二叉树。

 

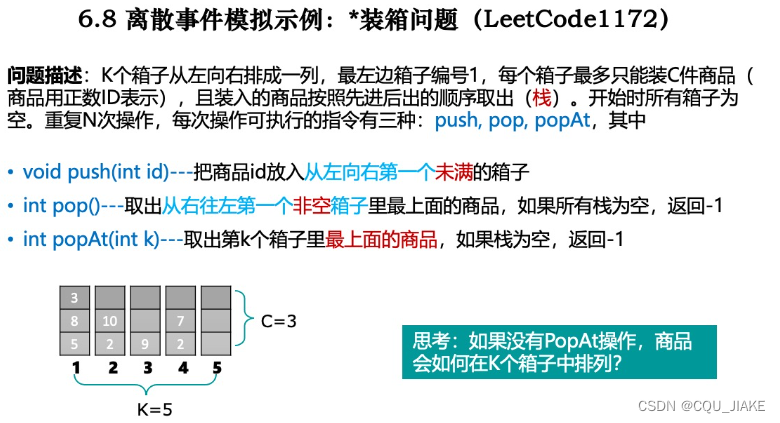
最大堆的堆顶是当前堆里最大的，最小堆的堆顶是当前堆里最小的

上图的应该是求第K小的，下面的表示整体剩下的，上面的表示选出来的k个，那么每次都是从下面流向上面，即下面此时最小的和上面此时最大的进行比较，如果小于，即调整；不然，就意味着已经选出了前k个小的，且，上面最大堆的堆顶就是第k小的