软考-des题目案例

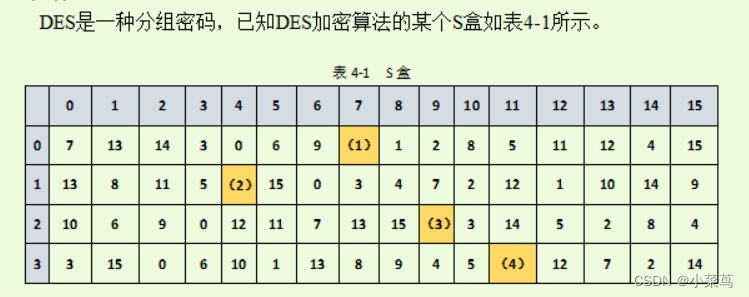
1.补全图片中的数字
（1）10 ，（2）6，（3）1，（4）11
2.初始置换简单计算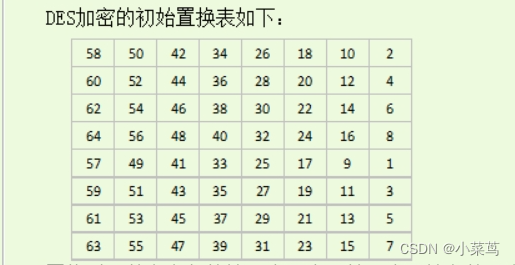

置换时，从左上角的第一个元素开始，表示输入的明文的第58位置换成输出的第1位，输入明文的第50位置换成输出的第2位，从左至右，从上往下，依次类推。DES加密时，对输入的64位明文首先进行初始置换操作。若置换输入的明文M=0123456789ABCDEF (16进制)，请计算其输出(16进制表示)
答：
首先对明文的每个字符进行二进制转换，转换为4位

0: 0000
1: 0001
2: 0010
3: 0011
4: 0100
5: 0101
6: 0110
7: 0111
8: 1000
9: 1001
A: 1010
B: 1011
C: 1100
D: 1101
E: 1110
F: 1111
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

因此，十六进制字符串 “0123456789ABCDEF” 转换为二进制表示为：0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111。
按照初始转换表：

输入数据：  0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
输出数据：  1101 1010 1001 1000 1111 1110 0011 0100 1011 1010 0011 0010 1111 1110 0001 0000
1
2

然后将输出数据转换为16进制：

D    A    9    8    F    E    3    4    B    A    3    2    F    E    1    0
1

3.如果有简化的DES版本，其明文输入为8比特，初始置换表IP如
IP:26314857，请给出其逆初始置换表。
答：
对于简化版的DES，给定初始置换表（IP）为 2, 6, 3, 1, 4, 8, 5, 7。

逆初始置换表（IP^-1）的计算步骤如下：

1. 创建一个长度为8的列表，初始值为0。即 [0, 0, 0, 0, 0, 0, 0, 0]。
2. 遍历初始置换表（IP），对于每个位置 i，在逆初始置换表中将该位置的值设置为 i。

根据给定的初始置换表（IP）为 2, 6, 3, 1, 4, 8, 5, 7，按照上述步骤计算逆初始置换表（IP^-1）：

1. 初始化逆初始置换表为 [0, 0, 0, 0, 0, 0, 0, 0]。
2. 遍历初始置换表（IP）：
   • 位置 1 的值为 2，因此在逆初始置换表的第2个位置（下标为1）设置值为1。
   • 位置 2 的值为 6，因此在逆初始置换表的第6个位置（下标为5）设置值为2。
   • 位置 3 的值为 3，因此在逆初始置换表的第3个位置（下标为2）设置值为3。
   • 位置 4 的值为 1，因此在逆初始置换表的第1个位置（下标为0）设置值为4。
   • 位置 5 的值为 4，因此在逆初始置换表的第4个位置（下标为3）设置值为5。
   • 位置 6 的值为 8，因此在逆初始置换表的第8个位置（下标为7）设置值为6。
   • 位置 7 的值为 5，因此在逆初始置换表的第5个位置（下标为4）设置值为7。
   • 位置 8 的值为 7，因此在逆初始置换表的第7个位置（下标为6）设置值为8。

最终，逆初始置换表（IP^-1）为 4, 1, 3, 5, 7, 2, 8, 6。