• Leetcode 23.旋转排序数组

    整数数组 nums 按升序排列，数组中的值 互不相同 。

    在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

    给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

    你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

    示例 1：

    输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

    示例 2：

    输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

    示例 3：

    输入：nums = [1], target = 0
输出：-1

    提示：

    • 1 <= nums.length <= 5000
    • -104 <= nums[i] <= 104
    • nums 中的每个值都 独一无二
    • 题目数据保证 nums 在预先未知的某个下标上进行了旋转
    • -104 <= target <= 104

    我的思考和分析过程

    一、信息

    1.整数数组 

    2.升序排列

    3.数组的值互不相同

    4.传值之前，num在预先位置的某个下标k上进行了旋转，使得数组变为

    5.例如看上面就知道怎么旋转了

    6.给我旋转后的数组和一个整数target

    7.我必须设计一个时间复杂度为O(log n)的算法解决这一个问题

    二、分析

    条件1：告诉我定义什么类型的数组

    答案：int型

    条件2：告诉我要对该数组进行排序

    答案：等等这里出现了问题就是我接收的数组是否需要我排序

    条件3：说实在的我看到条件3我连题目让我具体干什么我都没太搞懂

    条件5：应该只是让我们学会如何选择数组，首先先旋转数组。问题出现我们该如何旋转数组呢？或者说旋转数组有什么规律呢？

    条件6：告诉我旋转后要用target找到对应的值

    条件7：告诉我要用时间复杂度为Logn的算法解决这一个问题。但是哪些算法符合要求呢？那么问题就转化成找算法了

    三、步骤

    第一步 先对数组初始化然后排序（回忆起数组的知识：数组传送门）

    第二步 数组旋转（问题3出现：k既然是随意的那该如何使得k为随机的呢index吗？）

    第三步 通过target找到该值如果存在返回下标如果不存在那么retur-1（此处可以用二分搜索了很明显如果不记得的读者你们可以传送到这篇文章开启回忆：2.3 二分搜索技术）

    四、问题的出现

    问题1：该如何旋转数组呢？

    观察：

    通过观察我们不难发现其实数组旋转其实有两种情况

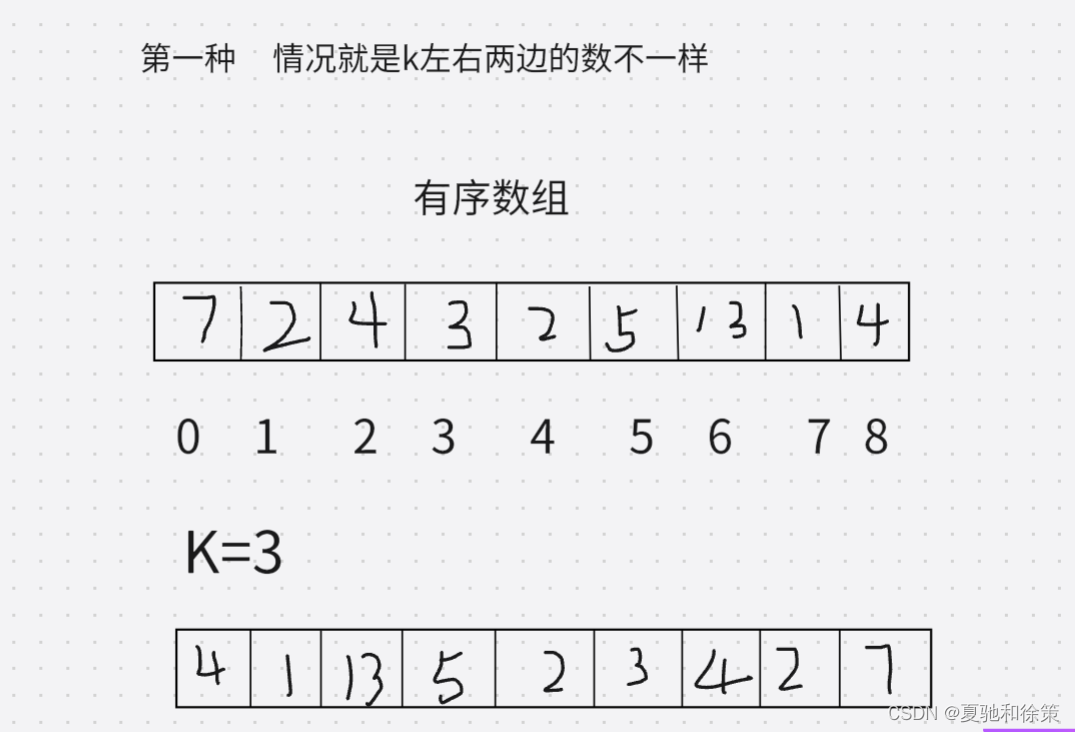
     对于第一种情况这种情况就会比较复杂，那么你就必须得把旋转轴上的数组先先和关于中心轴对称的然后

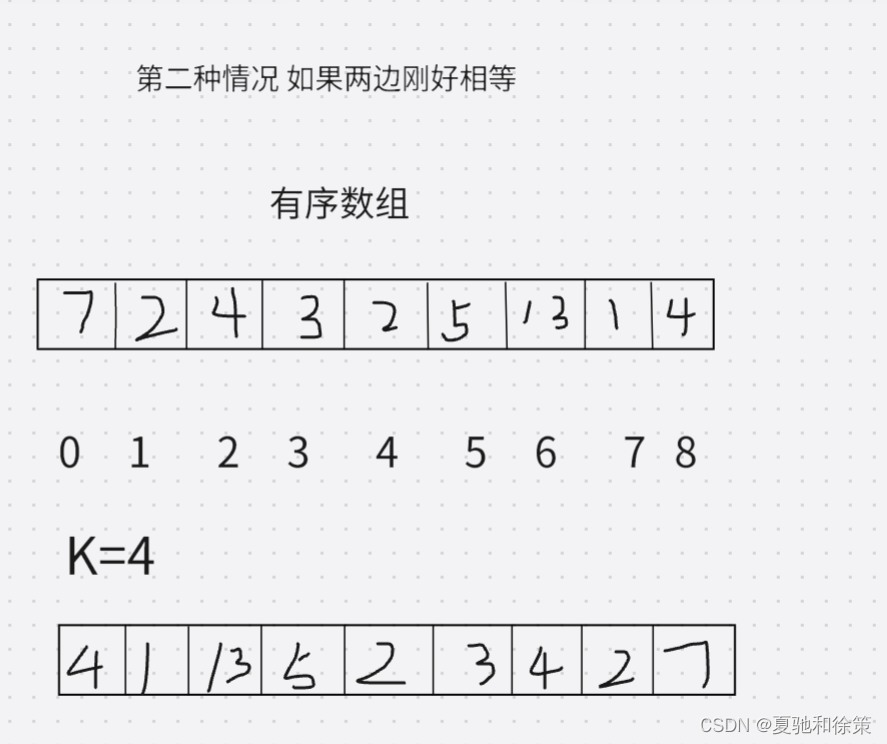
    第二种就是直接以轴调换位置即交换对称下标的值

    问题2：哪些算法满足时间复杂度为Log(n)

    具有时间复杂度 \(O(\log n)\) 的算法通常是高效的算法，它们能在对数时间内完成任务。这里有一些常见的 \(O(\log n)\) 时间复杂度的算法示例：

    1. **二分搜索算法（Binary Search）**：
       - 二分搜索是一个在已排序的数组中查找特定值的算法。每次迭代，它都会将搜索区间减半，直至找到目标值或搜索区间变为空。

    2. **快速幂算法（Exponentiation by Squaring）**：
       - 快速幂算法是一种计算 \(a^b\) 的高效算法。通过将问题分解为更小的子问题，它可以在 \(\log b\) 时间内完成计算。

    3. **平衡二叉搜索树操作（Balanced Binary Search Trees Operations）**：
       - 平衡二叉搜索树（如 AVL 树或红黑树）的插入、删除和查找操作通常具有 \(O(\log n)\) 的时间复杂度。

    4. **堆操作（Heap Operations）**：
       - 在二叉堆中，操作如插入和删除最小元素（或最大元素）通常具有 \(O(\log n)\) 的时间复杂度。

    5. **离散对数算法（Discrete Logarithm Algorithms）**：
       - 某些离散对数算法可以在 \(O(\log n)\) 时间复杂度内执行。

    6. **某些图算法（Certain Graph Algorithms）**：
       - 通过使用优先队列或其他数据结构，某些图算法（如 Dijkstra 的单源最短路径算法）可以优化到 \(O(\log n)\) 的时间复杂度。

    这些算法都利用了问题规模减半或问题分解的特点，以实现对数级的时间复杂度。

    问题3：如何进行数组排序

    答案：

    数组排序是编程和算法设计中常见的任务。有许多不同的排序算法，每种算法都有其特定的时间复杂度和空间复杂度。以下是一些常用的排序算法：

    1. **冒泡排序 (Bubble Sort)**:
       - 冒泡排序通过重复地遍历数组，比较相邻的元素并在必要时交换它们，来对数组进行排序。时间复杂度为 \(O(n^2)\)。

    2. **选择排序 (Selection Sort)**:
       - 选择排序每次从未排序的部分找到最小（或最大）的元素，将它放到已排序部分的末尾。时间复杂度为 \(O(n^2)\)。

    3. **插入排序 (Insertion Sort)**:
       - 插入排序通过构建有序序列，对未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。时间复杂度为 \(O(n^2)\)。

    4. **归并排序 (Merge Sort)**:
       - 归并排序是一个分治算法，它将数组分成两半，分别排序，然后合并两个已排序的半部分。时间复杂度为 \(O(n \log n)\)。

    5. **快速排序 (Quick Sort)**:
       - 快速排序通过选择一个基准元素并将数组分为两个子数组，一个包含比基准小的元素，另一个包含比基准大的元素，然后递归地排序两个子数组。时间复杂度为 \(O(n \log n)\)（平均情况）和 \(O(n^2)\)（最坏情况）。

    6. **堆排序 (Heap Sort)**:
       - 堆排序通过构建一个最大堆或最小堆，并重复地移除堆顶元素来对数组进行排序。时间复杂度为 \(O(n \log n)\)。

    7. **希尔排序 (Shell Sort)**:
       - 希尔排序是插入排序的一种变体，通过比较相隔特定间隔的元素来加速数组的排序。时间复杂度取决于间隔序列，通常为 \(O(n \log n)\) 或 \(O(n \log^2 n)\)。

    8. **基数排序 (Radix Sort)**:
       - 基数排序是一个非比较排序算法，通过分布式排序或计数排序对数组的每个数位进行排序。时间复杂度为 \(O(nk)\)，其中 \(k\) 是数位的数量。

    9. **桶排序 (Bucket Sort)**:
       - 桶排序将数组分成多个桶，然后使用另一个排序算法（通常是插入排序）对每个桶进行排序，最后将所有桶合并。时间复杂度为 \(O(n + k)\)，其中 \(k\) 是桶的数量。

    以上算法中，快速排序、归并排序和堆排序在实践中常用，因为它们的时间复杂度较低。不过，正确的选择取决于具体的应用场景和数据特点。例如，对于小数组或近乎有序的数组，插入排序可能是一个不错的选择。同时，也有一些现代的排序算法，例如 Timsort，它结合了插入排序和归并排序的特点，以达到在多种情况下都有良好性能的目的。

    大师的思考和分析过程

    一、信息

    1. 整数数组 `nums` 是升序排列的，但在某个未知下标 `k` 处进行了旋转。
    2. 需要找到目标值 `target` 在数组中的下标，如果不存在则返回 `-1`。
    3. 要设计的算法时间复杂度需为 \(O(\log n)\)。

    二、分析

    1. **条件的作用**:
       - 旋转的下标 `k` 将数组分成了两个升序的子数组，这意味着可以通过比较 `nums[mid]` 和 `nums[0]` 来确定 `mid` 是位于旋转的左侧还是右侧。
       - 由于数组是升序的，我们可以通过比较 `target` 和 `nums[mid]` 来确定 `target` 是在 `mid` 的左侧还是右侧。

    2. **思考过程**:
       - **思路1**：遍历整个数组查找 `target`。但这样的时间复杂度为 \(O(n)\)，不符合题目的要求。
       - **思路2**：二分搜索。由于数组是升序且唯一，二分搜索是最合适的。但是由于数组被旋转，需要修改标准的二分搜索算法来处理这种情况。

    通过以上分析，二分搜索是最合适的解决方案。

    3. **分析过程**:
       - 在标准的二分搜索中，我们比较 `target` 和 `nums[mid]`，并根据 `target` 是大于还是小于 `nums[mid]` 来决定是在左侧还是右侧搜索。
       - 但是在这个问题中，由于旋转，我们需要确定 `mid` 是在旋转的左侧还是右侧，然后再确定 `target` 是在 `mid` 的左侧还是右侧。

    三、算法实现步骤

    1. 初始化两个指针 `left` 和 `right` 为 `0` 和 `nums.length - 1`。
    2. 当 `left <= right` 时，执行以下步骤：
       1. 计算 `mid = (left + right) / 2`。
       2. 如果 `nums[mid]` 等于 `target`，返回 `mid`。
       3. 如果 `nums[mid]` 大于等于 `nums[left]`，则 `mid` 在旋转的左侧：
          - 如果 `target` 在 `nums[left]` 和 `nums[mid]` 之间，则设置 `right = mid - 1`，否则设置 `left = mid + 1`。
       4. 否则，`mid` 在旋转的右侧：
          - 如果 `target` 在 `nums[mid]` 和 `nums[right]` 之间，则设置 `left = mid + 1`，否则设置 `right = mid - 1`。
    3. 如果循环结束时没有找到 `target`，返回 `-1`。

    四、实现过程中遇到的问题

    - 需要正确处理边界条件，例如当 `left` 和 `right` 指针相遇时，以及当 `target` 不在数组中时。
    - 需要正确判断 `mid` 是在旋转的左侧还是右侧，并根据此来更新 `left` 和 `right` 指针。

    这个问题的核心是利用二分搜索的高效性，并通过适当的条件判断来处理数组的旋转特点，以在 \(O(\log n)\) 的时间复杂度内找到 `target` 的位置。

    大师对我的评价：

    你的思考和分析过程很清晰，每个步骤都有明确的目标和问题识别，这是值得肯定的。同时，你的分析过程中展示了对于问题背景和相关算法的理解。但还有一些方面可以提高和优化，具体如下：

    1. **问题理解**:
       - 在分析过程的开始阶段，对问题的理解有些困惑，可能需要更多时间去理解题目的要求和背景。在这种情况下，可能需要多读几遍题目或查找相关的背景信息来帮助理解。

    2. **旋转数组的理解**:
       - 在旋转数组的理解上，似乎有些不清楚。实际上，旋转数组指的是将数组的前k个元素移到数组的末尾，这个k是旋转的点。在题目中，这个旋转是已经完成的，我们不需要再去进行旋转，而是需要在旋转后的数组中找到目标值。

    3. **排序算法的理解**:
       - 在分析过程中，你花了一些时间探讨了不同的排序算法，虽然这对于问题解决不是必需的，但这显示了你对不同算法的理解。但是，对于这个特定问题，我们不需要对数组进行排序，因为数组在旋转前已经是排序好的。

    4. **算法选择**:
       - 二分搜索是正确的方向，但在应用它时，需要考虑到数组的旋转。标准的二分搜索算法需要一个排序的数组，但由于旋转，我们需要修改二分搜索的逻辑以适应旋转的情况。

    5. **步骤划分**:
       - 在步骤划分时，可能需要更清楚地描述每个步骤的目的和执行方法。例如，在进行二分搜索时，应该明确在哪个条件下搜索左半部分或右半部分，以及如何更新搜索范围。

    6. **问题归纳和解决**:
       - 在分析过程中提出了一些问题，但没有明确的解决方案或策略。在实际操作中，可能需要更具体的解决步骤和策略来解决这些问题。

    7. **参考资料链接**:
       - 你提供了一些传送门和文章链接，这很好，可以帮助读者更好地理解和学习。但在实际解决问题时，也可以尝试直接解释或总结相关的知识点，以使分析过程更为完整。

    在将来的分析过程中，你可以尝试更深入地理解问题背景，明确每个步骤的目的，以及提供更具体的解决方案和策略。同时，保持对问题的好奇心和探索精神是非常好的，这会帮助你在解决问题时有更多的创意和思路。

    五、算法实现

    我的答案：

    我没做出来第一次哈哈哈哈

    大师的答案：

    C语言：

    1. #include 
    2.  
    3. int search(int* nums, int numsSize, int target) {
    4.     int left = 0;
    5.     int right = numsSize - 1;
    6.     
    7.     while (left <= right) {
    8.         int mid = (left + right) / 2;
    9.         
    10.         // If the target value is found, return the index
    11.         if (nums[mid] == target) {
    12.             return mid;
    13.         }
    14.         
    15.         // Determine which side of the array is sorted
    16.         if (nums[left] <= nums[mid]) {  // Left side is sorted
    17.             // If target is within the sorted left side, search left
    18.             if (nums[left] <= target && target < nums[mid]) {
    19.                 right = mid - 1;
    20.             } else {  // Otherwise, search right
    21.                 left = mid + 1;
    22.             }
    23.         } else {  // Right side is sorted
    24.             // If target is within the sorted right side, search right
    25.             if (nums[mid] < target && target <= nums[right]) {
    26.                 left = mid + 1;
    27.             } else {  // Otherwise, search left
    28.                 right = mid - 1;
    29.             }
    30.         }
    31.     }
    32.     
    33.     return -1;  // Target value not found
    34. }
    35.  
    36. int main() {
    37.     int nums[] = {4, 5, 6, 7, 0, 1, 2};
    38.     int target = 0;
    39.     int numsSize = 7;
    40.     int result = search(nums, numsSize, target);
    41.     printf("The index of the target value is: %d\n", result);
    42.     return 0;
    43. }

     代码解释：

    在这个代码中，search 函数接受一个整数数组 nums、数组的大小 numsSize 和目标值 target 作为参数，并返回目标值在数组中的索引。如果目标值不存在于数组中，函数返回 -1。在 main 函数中，我们创建了一个示例数组和目标值，并调用了 search 函数来查找目标值的索引。

    C++：

    1. #include 
    2. #include 
    3. using namespace std;
    4.  
    5. class Solution {
    6. public:
    7.     int search(vector<int>& nums, int target) {
    8.         int left = 0;
    9.         int right = nums.size() - 1;
    10.         
    11.         while (left <= right) {
    12.             int mid = (left + right) / 2;
    13.             
    14.             // 如果找到目标值，返回索引
    15.             if (nums[mid] == target) {
    16.                 return mid;
    17.             }
    18.             
    19.             // 确定数组的哪一侧是有序的
    20.             if (nums[left] <= nums[mid]) {  // 左侧有序
    21.                 // 如果目标值在有序的左侧，继续在左侧搜索
    22.                 if (nums[left] <= target && target < nums[mid]) {
    23.                     right = mid - 1;
    24.                 } else {  // 否则，在右侧搜索
    25.                     left = mid + 1;
    26.                 }
    27.             } else {  // 右侧有序
    28.                 // 如果目标值在有序的右侧，继续在右侧搜索
    29.                 if (nums[mid] < target && target <= nums[right]) {
    30.                     left = mid + 1;
    31.                 } else {  // 否则，在左侧搜索
    32.                     right = mid - 1;
    33.                 }
    34.             }
    35.         }
    36.         
    37.         return -1;  // 未找到目标值
    38.     }
    39. };
    40.  
    41. int main() {
    42.     Solution solution;
    43.     vector<int> nums = {4, 5, 6, 7, 0, 1, 2};
    44.     int target = 0;
    45.     int result = solution.search(nums, target);
    46.     cout << "The index of the target value is: " << result << endl;
    47.     return 0;
    48. }

    JAVA：
     

    1. public class Solution {
    2.     public int search(int[] nums, int target) {
    3.         int left = 0;
    4.         int right = nums.length - 1;
    5.         
    6.         while (left <= right) {
    7.             int mid = (left + right) / 2;
    8.             
    9.             // 如果找到目标值，返回索引
    10.             if (nums[mid] == target) {
    11.                 return mid;
    12.             }
    13.             
    14.             // 确定数组的哪一侧是有序的
    15.             if (nums[left] <= nums[mid]) {  // 左侧有序
    16.                 // 如果目标值在有序的左侧，继续在左侧搜索
    17.                 if (nums[left] <= target && target < nums[mid]) {
    18.                     right = mid - 1;
    19.                 } else {  // 否则，在右侧搜索
    20.                     left = mid + 1;
    21.                 }
    22.             } else {  // 右侧有序
    23.                 // 如果目标值在有序的右侧，继续在右侧搜索
    24.                 if (nums[mid] < target && target <= nums[right]) {
    25.                     left = mid + 1;
    26.                 } else {  // 否则，在左侧搜索
    27.                     right = mid - 1;
    28.                 }
    29.             }
    30.         }
    31.         
    32.         return -1;  // 未找到目标值
    33.     }
    34.  
    35.     public static void main(String[] args) {
    36.         Solution solution = new Solution();
    37.         int[] nums = {4, 5, 6, 7, 0, 1, 2};
    38.         int target = 0;
    39.         int result = solution.search(nums, target);
    40.         System.out.println("The index of the target value is: " + result);
    41.     }
    42. }

    Leetcode 官方题解：

    方法一：二分查找
    思路和算法

    对于有序数组，可以使用二分查找的方法查找元素。

    但是这道题中，数组本身不是有序的，进行旋转后只保证了数组的局部是有序的，这还能进行二分查找吗？答案是可以的。

    可以发现的是，我们将数组从中间分开成左右两部分的时候，一定有一部分的数组是有序的。拿示例来看，我们从 6 这个位置分开以后数组变成了 [4, 5, 6] 和 [7, 0, 1, 2] 两个部分，其中左边 [4, 5, 6] 这个部分的数组是有序的，其他也是如此。

    这启示我们可以在常规二分查找的时候查看当前 mid 为分割位置分割出来的两个部分 [l, mid] 和 [mid + 1, r] 哪个部分是有序的，并根据有序的那个部分确定我们该如何改变二分查找的上下界，因为我们能够根据有序的那部分判断出 target 在不在这个部分：

    如果 [l, mid - 1] 是有序数组，且 target 的大小满足 [nums[l],nums[mid])[\textit{nums}[l],\textit{nums}[mid])[nums[l],nums[mid])，则我们应该将搜索范围缩小至 [l, mid - 1]，否则在 [mid + 1, r] 中寻找。
    如果 [mid, r] 是有序数组，且 target 的大小满足 (nums[mid+1],nums[r]](\textit{nums}[mid+1],\textit{nums}[r]](nums[mid+1],nums[r]]，则我们应该将搜索范围缩小至 [mid + 1, r]，否则在 [l, mid - 1] 中寻找。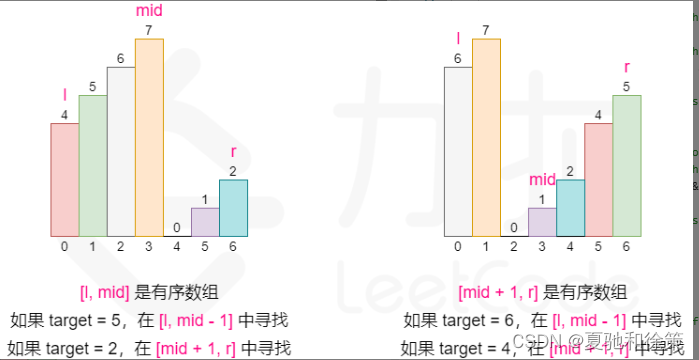


    需要注意的是，二分的写法有很多种，所以在判断 target 大小与有序部分的关系的时候可能会出现细节上的差别。

    1. class Solution {
    2. public:
    3.     int search(vector<int>& nums, int target) {
    4.         int n = (int)nums.size();
    5.         if (!n) {
    6.             return -1;
    7.         }
    8.         if (n == 1) {
    9.             return nums[0] == target ? 0 : -1;
    10.         }
    11.         int l = 0, r = n - 1;
    12.         while (l <= r) {
    13.             int mid = (l + r) / 2;
    14.             if (nums[mid] == target) return mid;
    15.             if (nums[0] <= nums[mid]) {
    16.                 if (nums[0] <= target && target < nums[mid]) {
    17.                     r = mid - 1;
    18.                 } else {
    19.                     l = mid + 1;
    20.                 }
    21.             } else {
    22.                 if (nums[mid] < target && target <= nums[n - 1]) {
    23.                     l = mid + 1;
    24.                 } else {
    25.                     r = mid - 1;
    26.                 }
    27.             }
    28.         }
    29.         return -1;
    30.     }
    31. };
    32.

    总结：

    从这道题目中，我们可以学到以下几点：

    1. **二分搜索应用**:
        - 这道题是二分搜索算法的变体应用，通过判断旋转点在哪一侧来决定搜索的方向。二分搜索是一种非常高效的算法，适用于已排序或部分有序的数据结构，其时间复杂度为 \(O(\log n)\)。

    2. **条件判断与边界处理**:
        - 在解决问题时，要精确判断和处理边界条件。例如，判断旋转的分界点，以及在二分搜索过程中更新 left 和 right 指针的位置。

    3. **算法设计思维**:
        - 通过分析问题，识别可以利用的模式（如有序、旋转等），并设计出解决问题的算法。这是解决类似问题的基础。

    4. **代码的简洁与清晰**:
        - 良好的代码结构和清晰的逻辑对于解决问题和后续的代码维护是非常重要的。例如，通过循环和条件判断来清晰地展现二分搜索的逻辑。

    5. **问题分析与解决策略**:
        - 在面对问题时，先进行分析，理解问题的需求和约束条件，然后再制定解决策略。例如，分析旋转数组的特点，然后选择二分搜索作为解决策略。

    6. **测试与验证**:
        - 在实现算法后，通过多组测试用例来验证算法的正确性和完整性是非常重要的。

    7. **多语言实现**:
        - 通过尝试在多种编程语言（如 C、C++、Java 等）中实现同一个算法，可以增强对编程语言和算法的理解。

    通过解决这类问题，你可以练习和加深对算法和数据结构的理解，提升解决实际编程问题的能力。

  • 相关阅读:
    如何选择适合自己的跨境商城源码
    idea注释代码三种方式
    接口测试1
    合约升级标准 ERC2535 的设计解析和不足
    Linux基本使用和web程序部署
    1.1 大数据简介-hadoop-最全最完整的保姆级的java大数据学习资料
    软考高级系统架构设计师系列之：计算机与网络基础知识汇总
    uniapp新版微信小程序用户隐私协议授权
    Android MediaCodec 简明教程（九）：使用 MediaCodec 解码到纹理，使用 OpenGL ES 进行处理，并编码为 MP4 文件
    vue3 框架学习概念笔记
  • 原文地址：https://blog.csdn.net/tang7mj/article/details/133757765