-
python中pytorch的广播机制——Broadcasting
广播机制
numpy 在算术运算期间采用“广播”来处理具有不同形状的 array ,即将较小的阵列在较大的阵列上“广播”,以便它们具有兼容的形状。Broadcasting是一种没有copy数据的expand
- 不过两个维度不相同,在前面插入维度1
- 扩张维度1到相同的维度
例如:Feature maps:[4,32,14,14]
Bias:[32,1,1]=>[1,32,1,1]=>[4,32,14,14]A:[32,1,1]=>[1,32,1,1]=>[4,32,14,14]
B:[4,32,14,14]
这里就可以进行相同维度的相加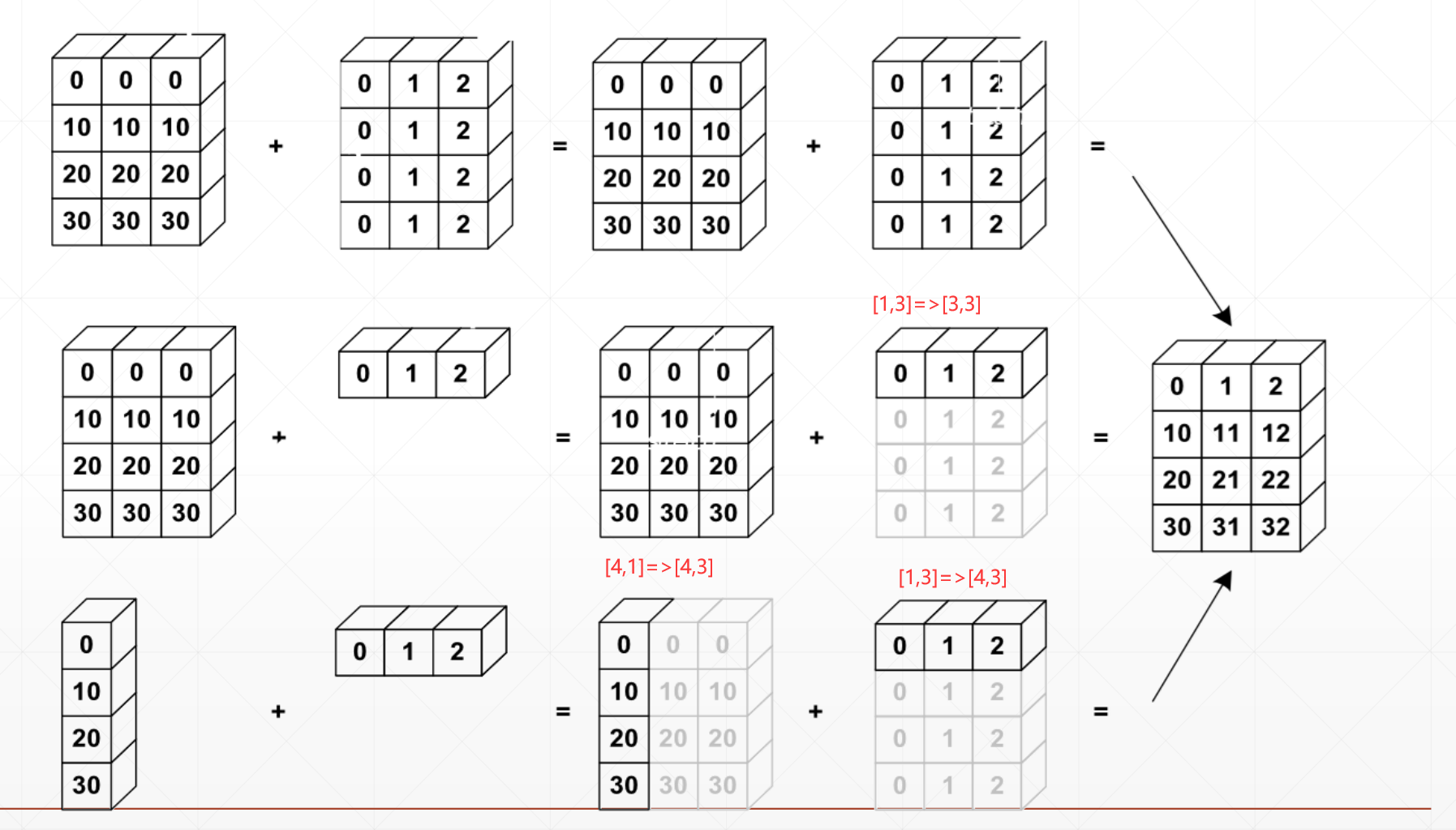
比如说一个[4,1]+[1,2]
那么这个[4,1]可以再复制列变为[4,2]
[1,2]可以再复制4行变为[4,2]首先用1将那个小的维度的tensor扩展成大的维度相同的维度,然后将1扩张成两者的相同维度,如果有两个维度不相同,并且都不是1的话,则不能broadcasting

广播规则
当对两个 array 进行操作时,numpy 会逐元素比较它们的形状。从尾(即最右边)维度开始,然后向左逐渐比较。只有当两个维度 1)相等 or 2)其中一个维度是1 时,这两个维度才会被认为是兼容。
如果不满足这些条件,则会抛出 ValueError:operands could not be broadcast together 异常,表明 array 的形状不兼容。最终结果 array 的每个维度尽可能不为 1 ,是两个操作数各个维度中较大的值 。
例如,有一个 256x256x3 的 RGB 值图片 array ,需要将图像中的每种颜色缩放不同的值,此时可以将图像乘以具有 3 个值的一维 array 。根据广播规则排列这两个 array 的尾维度大小,是兼容的:
图片(3d array): 256 x 256 x 3
缩放(1d array): 3
结果(3d array): 256 x 256 x 3当比较的任一维度是 1 时,使用另一个,也就是说,大小为 1 的维度被拉伸或“复制”以匹配另一个维度。
在以下示例中,A 和 B 数组都有长度为 1 的维度,在广播操作期间扩展为更大的大小:A (4d array): 8 x 1 x 6 x 1
B (3d array): 7 x 1 x 5
result (4d array): 8 x 7 x 6 x 5以二维为例,更加方便的解释“广播”:
已知 a.shape 是(5,1),b.shape 是(1,6),c.shape 是(6,),d.shape 是(), d 是一个标量, a, b, c,和 d 都可以“广播”到维度 (5,6);a “广播”为一个 (5,6) array ,其中 a[:,0] 被“广播”到其他列,
b “广播”为一个 (5,6) array ,其中 b[0,:] 被广播到其他行,
c 类似于 (1,6) array ,其中 c[:] 广播到每一行,
d 是标量,“广播”为 (5,6) array ,其中每个元素都一样,重复d值。
- A (2d array): 2 x 1
- B (3d array): 8 x 4 x 3 # 倒数第二个维度不兼容
- >>> a = np.array([[ 0.0, 0.0, 0.0],
- ... [10.0, 10.0, 10.0],
- ... [20.0, 20.0, 20.0],
- ... [30.0, 30.0, 30.0]])
- >>> b = np.array([1.0, 2.0, 3.0])
- >>> a + b
- array([[ 1., 2., 3.],
- [11., 12., 13.],
- [21., 22., 23.],
- [31., 32., 33.]])
- >>> b = np.array([1.0, 2.0, 3.0, 4.0])
- >>> a + b
- Traceback (most recent call last):
- ValueError: operands could not be broadcast together with shapes (4,3) (4,)


在某些情况下,广播会拉伸两个 array 以形成一个大于任何一个初始 array 的结果 array 。
- >>> a = np.array([0.0, 10.0, 20.0, 30.0])
- >>> b = np.array([1.0, 2.0, 3.0])
- >>> a[:, np.newaxis] + b
- array([[ 1., 2., 3.],
- [11., 12., 13.],
- [21., 22., 23.],
- [31., 32., 33.]])

newaxis运算符将新轴插入到 a 中,使其成为二维 4x1 array 。将 4x1 array 与形状为 (3,) 的 b 组合,产生一个 4x3 array 。这里注意要都从右端进行匹配:
A:[ ]
B: [ ]
就是这样补充
我们看个例子吧:- a=torch.randn(2,3,4)
- b=torch.randn(2,3)
- a+b
- #The size of tensor a (4) must match the size of tensor b (3) at non-singleton dimension 2
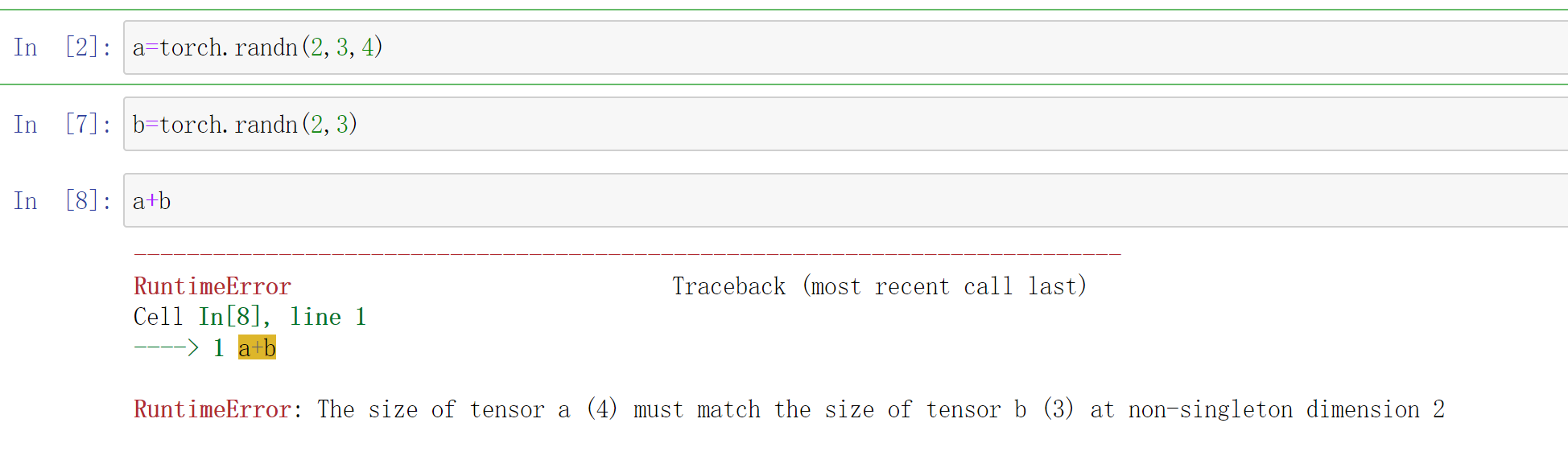
但是这样是可以的
也就是(2,3,4)+(2,3)是不可以的,(2,3,4)+(3,4)是可以的,因为他们是右看齐的。Situation 1:
▪ [4, 32, 14, 14]
▪ [1, 32, 1, 1] => [4, 32, 14, 14]Situation 2
▪ [4, 32, 14, 14]
▪ [14, 14] => [1, 1, 14, 14] => [4, 32, 14, 14]Situation 3
▪ [4, 32, 14, 14]
▪ [2, 32, 14, 14]
▪ Dim 0 has dim, can NOT insert and expand to same
▪ Dim 0 has distinct dim, NOT size 1
▪ NOT broadcasting-ableSituation 4
▪ [4, 32, 14, 14]
▪ [4, 32, 14]
这样是不行的,因为我们要右看齐,match from
last dimSituation 5
▪ [4, 3, 32, 32]
▪ + [32, 32]
▪ + [3, 1, 1]
▪ + [1, 1, 1, 1]
这都是可以的 -
相关阅读:
影视级跨平台视频制作技术的落地实践
计算机毕业设计Java滴答拍摄影项目(源码+系统+mysql数据库+lw文档)
数据仓库中常用的元数据管理系统
C++试卷(程序设计题)
矿区安全检查VR模拟仿真培训系统更全面、生动有效
Flink面试题
JavaScript中的代理对象(proxy)
Docker 安装部署 Gitlab 存储路径迁移
JavaScript代码执行
开始投简历了
- 原文地址:https://blog.csdn.net/laosao_66/article/details/133757449