【数据结构--排序】堆排序

💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤
📃个人主页 ：阿然成长日记 👈点击可跳转
📆 个人专栏： 🔹数据结构与算法🔹C语言进阶
🚩 不能则学，不知则问，耻于问人，决无长进
🍭 🍯 🍎 🍏 🍊 🍋 🍒 🍇 🍉 🍓 🍑 🍈 🍌 🍐 🍍

堆排序

一、🌱排降序

口诀：排降序，建小堆

1.思路：

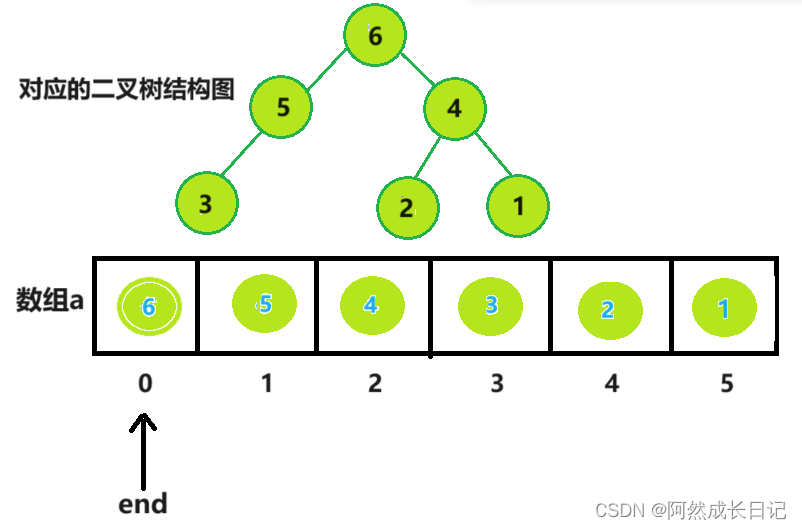
（1）首先使用从下到上的方法建立小堆；如下图

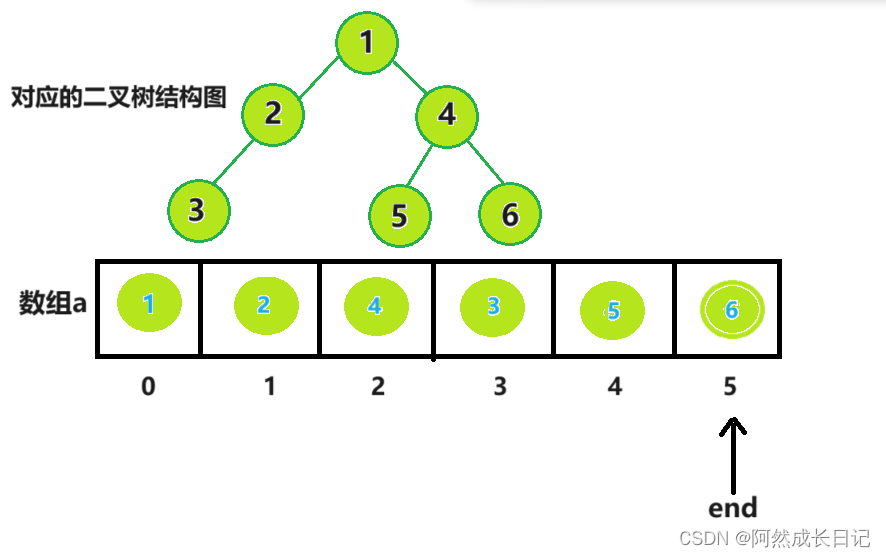
（2）堆顶与最后一个节点交换，由于是小堆，堆顶是最小值。交换后，就选出了最小值并将其放到数组的组后位置，

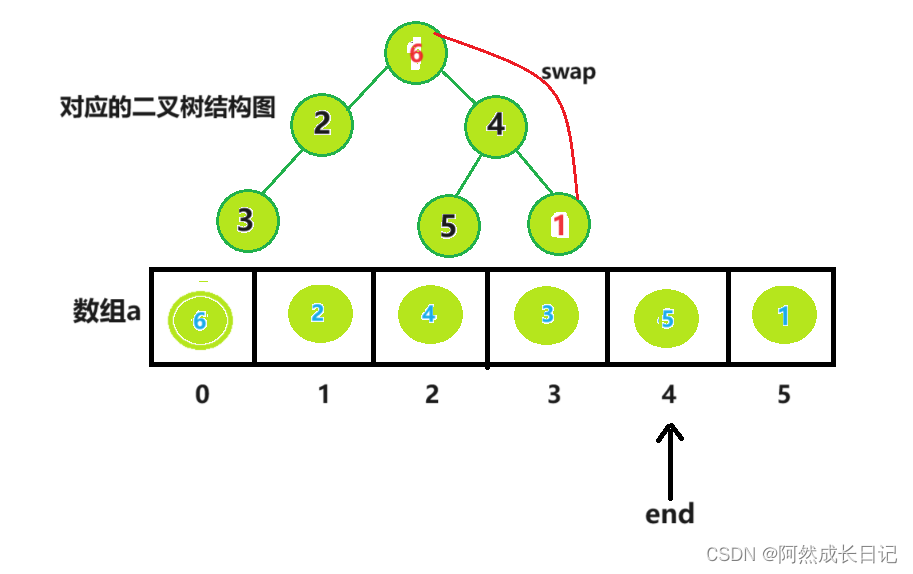
（3）.将堆的长度减1【end–】（数组长度减1）。
（4).在对剩下的堆进行基于小堆的向下调整，从而将第二小的数调整到了堆顶。

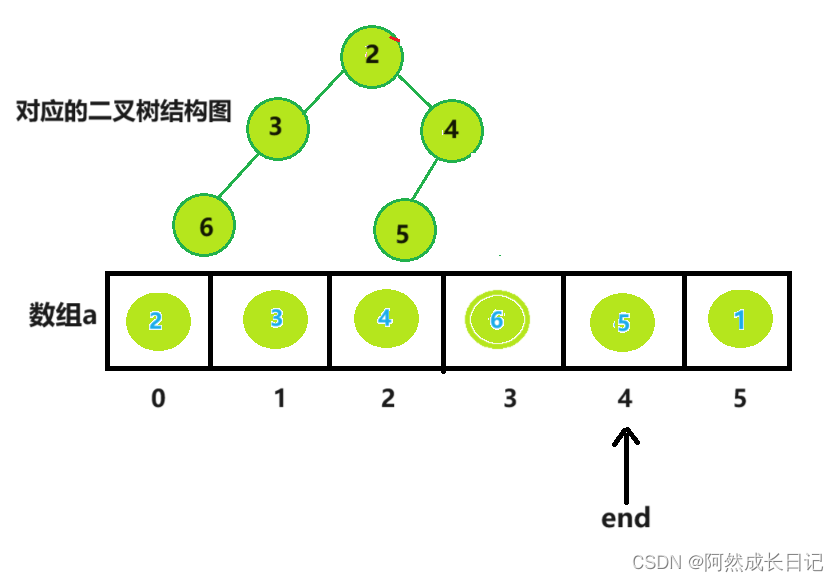
重复步骤2.3.4，end一直减到0；
4.最后，这个原本存储小堆的数组，就变成了一个从小到大的降序数组。

2.代码实现：

1.交换

//交换
void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}
1
2
3
4
5
6
7

2.修改AdjustDown(a, end, 0);为调小堆

基于小堆的向下调整
```c

void AdjustDownxiao(int* a, int n, int parent)
{
	int child = parent * 2 + 1;
	//一直交换到数的最后，也就是数组的最后一个位置
	while (child < n)
	{
		if (child + 1 < n && a[child + 1] < a[child])
		{
			child++;
		}
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			// 继续往下调整
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			return;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

3.排降序

void HeapSortDES(int* a, int n)
{
	//建立小堆
	for (int i = (n-1-1)/2; i >= 0; i--)
	{
		AdjustDownxiao(a, n, i);
	}

	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		//每次调整从根0到end，end每次会减1。
		AdjustDownxiao(a, end, 0);
		--end;
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

3.测试结果

4.总代码

//交换
void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}
//基于小堆的向下调整
void AdjustDownxiao(int* a, int n, int parent)
{
	int child = parent * 2 + 1;
	//一直交换到数的最后，也就是数组的最后一个位置
	while (child < n)
	{
		if (child + 1 < n && a[child + 1] < a[child])
		{
			child++;
		}
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			// 继续往下调整
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			return;
		}
	}
}

//降序
void HeapSortDES(int* a, int n)
{
	//建立小堆
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDownxiao(a, n, i);
	}

	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		//每次调整从根0到end，end每次会减1。
		AdjustDownxiao(a, end, 0);
		end--;
	}
}


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

二、🌸排升序

口诀：排升序，建大堆

意思是：想要将数组的顺序变成一个升序的，那么可以建立一个大堆存在数组中，在对堆进行调整。即可将数组变成一个升序数组。

1.思路：

首先使用从下到上的方法建立大堆；
1.堆顶与最后一个节点交换，由于是大堆，堆顶是最大值。交换后，就选出了最大值并将其放到数组的组后位置，
2.并将堆的长度减1（数组长度减1）。
3.在对剩下的堆进行基于大堆的向下调整，从而将第二大的数调整到了堆顶。
4.最后，这个原本存储大堆的数组，就变成了一个从小到大的升序数组。

2.代码实现：

1.交换

//交换
void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}
1
2
3
4
5
6
7

2.基于大堆的向下调整

//基于大堆的向下调整
void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;
	//一直交换到数的最后，也就是数组的最后一个位置
	while (child < n)
	{
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child++;
		}
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			// 继续往下调整
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			return;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

3.排升序

//排升序
void HeapSortASC(int* a, int n)
{
	//建立大堆
	for (int i = (n-1-1)/2; i >= 0; i--)
	{
		AdjustDown(a, n, i);
	}

	int end = n - 1;
	while (end > 0)
	{
		swap(&a[0], &a[end]);
		//每次调整从根0到end，end每次会减1。
		AdjustDown(a, end, 0);
		end--;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

3.测试结果：

4.总代码

//交换
void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}
void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;
	//一直交换到数的最后，也就是数组的最后一个位置
	while (child < n)
	{
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child++;
		}
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			// 继续往下调整
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			return;
		}
	}
}




//升序
void HeapSortASC(int* a, int n)
{
	//建立小堆
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, n, i);
	}

	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		//每次调整从根0到end，end每次会减1。
		AdjustDown(a, end, 0);
		end--;
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

三、堆排序的时间复杂度

堆排序分两步：1.建堆（使用时间复杂度更低的向下调整建堆）2.排序

向下调整建堆的时间复杂度为O(n);
n-1次删除操作的时间复杂度为O(nlogn)；
所以总操作时间复杂度为O(nlogn)