高精地图_语义地图_众包地图相关论文笔记

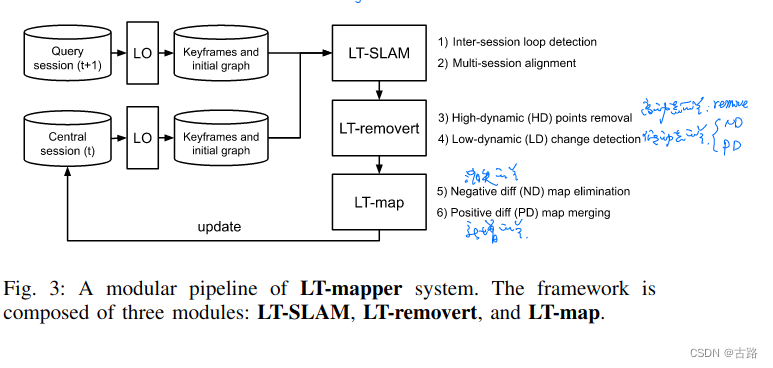
1.20220618_LT-mapper: A Modular Framework for LiDAR-based Lifelong Mapping

• 2021
• 3d-Lidar构建long-term地图
• 分为
  • SLAM模块（每个session的点云地图通过关键帧构建，对不同session的关键帧进行anchor node检测，基于anchor帧构建的闭环因子实现Multi-session之间offset的修正，在保证单个session pose最优的情况下，Multi-session之间的pose也是对齐的）
  • 点云移除模块（检测变化的点云进行策略性的增加与删除）
  • 地图管理模块
• 代码开源，使用GTSAM优化

2.20220623_Road Mapping and Localization using Sparse Semantic VisualFeatures

• 2021
• 文章主要实现了基于道路路标的SLAM，包括回环检测，作者来自阿里。
• 地面特征匹配使用匈牙利算法、电线杆等匹配使用光流法
• 使用B样条拟合道路线
• 是真的把语义信息纳入到状态变量进行一起优化的系统
• 工作量有点大

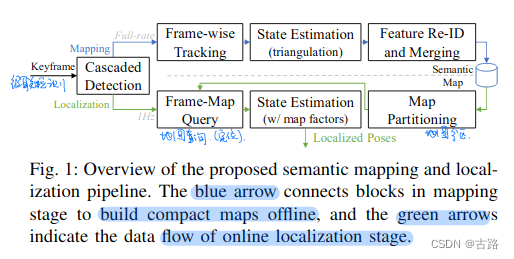
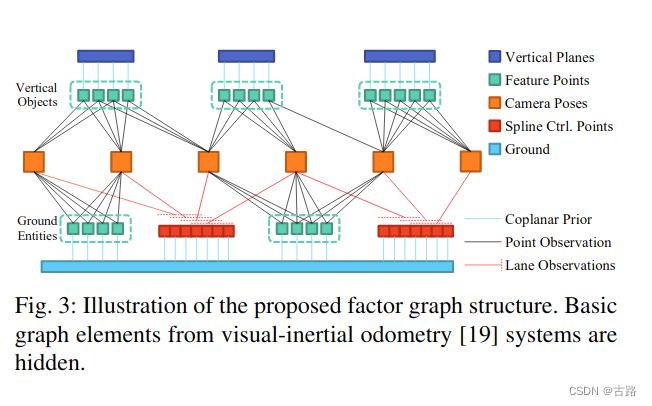
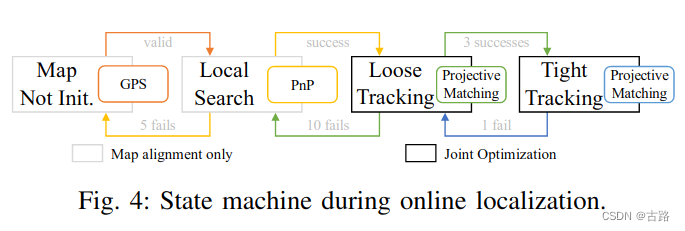
3.20220629_A General Framework for Lifelong Localization and Mapping in Changing Environment

• 2021
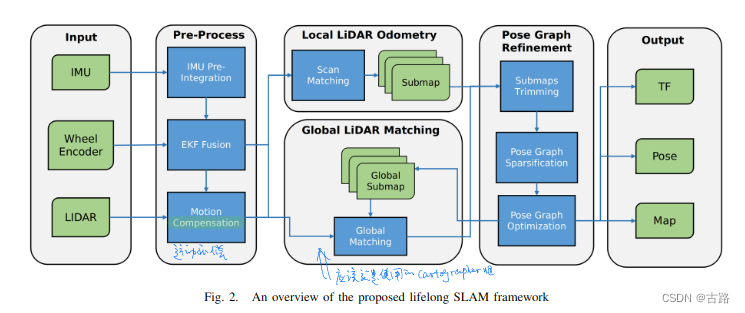
• 高仙机器人的life-long SLAM，可以看出是基于cartographer的工作
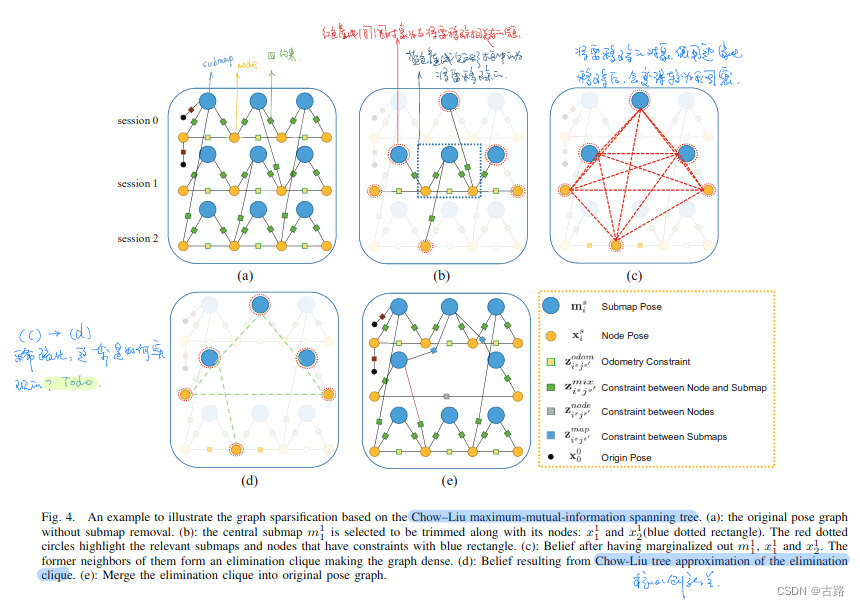
• 最核心的贡献是，在移除子图时使用边缘化法进行子图的移除，但是移除后会使得图模型变得稠密，于是采用 Chow-Liu Tree 进行图模型近似稀疏化。这一点应该是在life-long主题必备的。
• 还有一篇同时期的工作也是用的这个算法原理。

4.20220701_Geometry-based Graph Pruning for Lifelong SLAM

• 2021
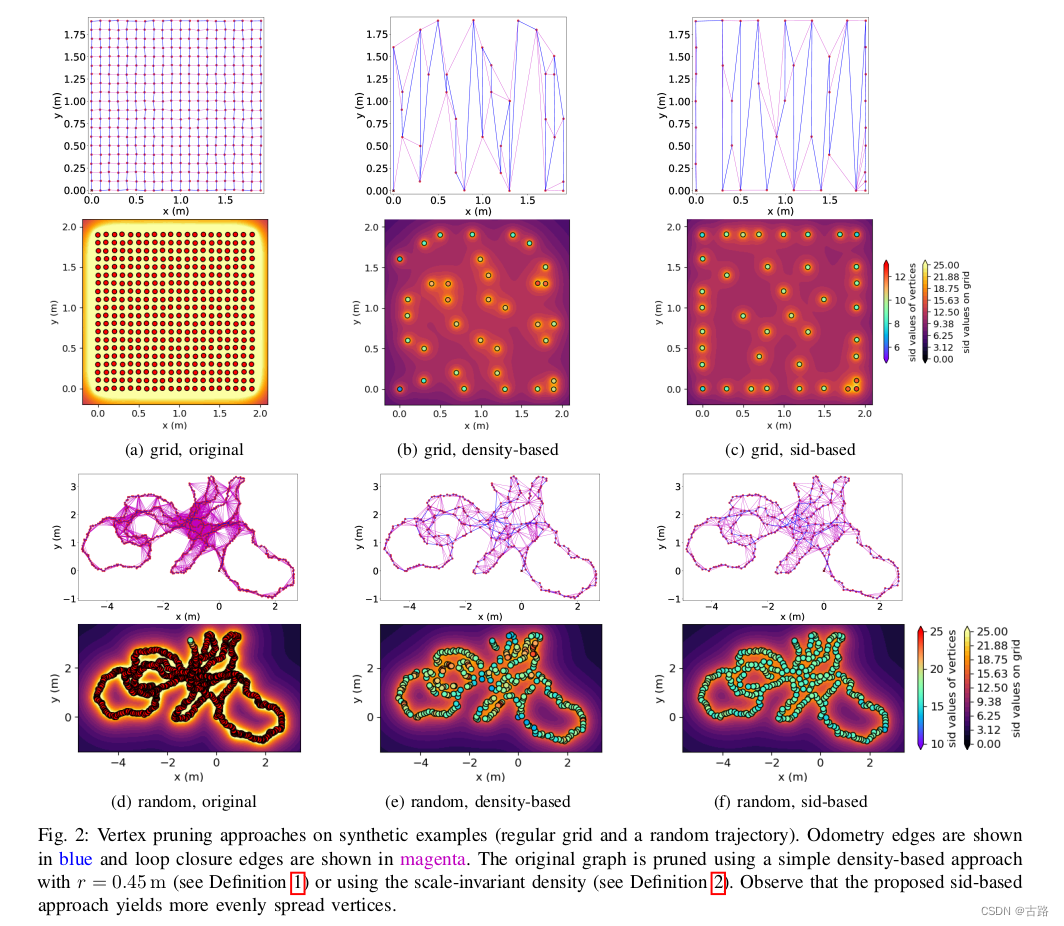
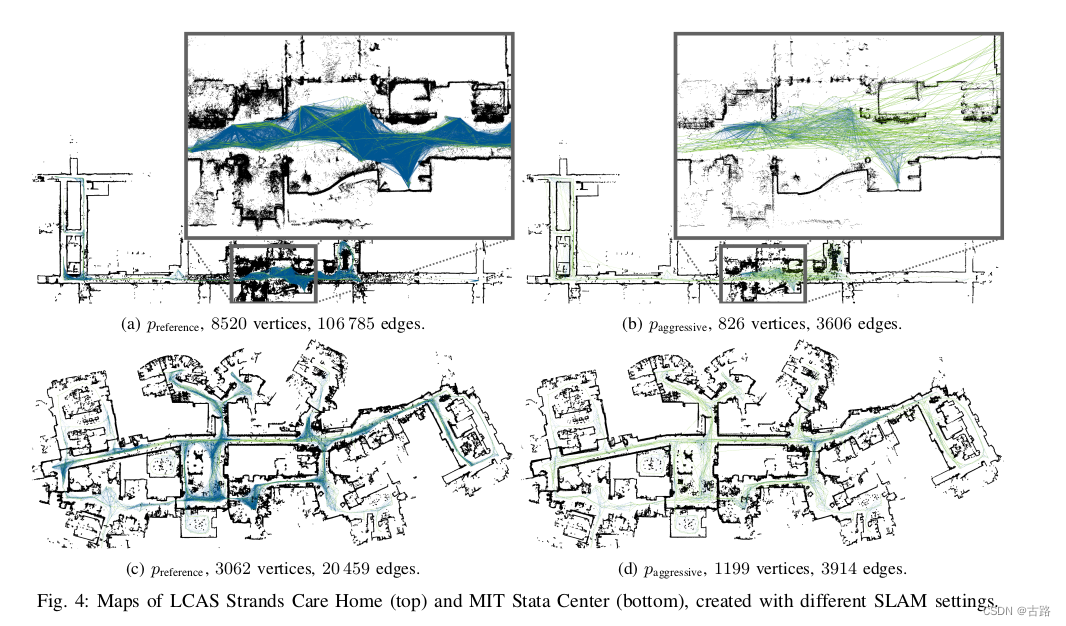
• 同高仙机器人论文，使用Chow-Liu Tree 进行稀疏化
• 对于频繁建图的场景很实用，可以借鉴。

5.20220703_Mapping and Localization using Semantic Road Marking withCentimeter-level Accuracy in Indoor Parking Lots

• 2019
• IMU+轮速计进行航迹推算
• 环视进行语义分割（选定ROI防止边缘区域畸变过大）
• 子图里面校正DR、回环全局优化
• 利用DR数据进行图像拼接、利用语义信息进行点云融合
• 值得学习的算法：
  • 点云融合算法（避免点云过多出现问题）
  • 语义ICP算法

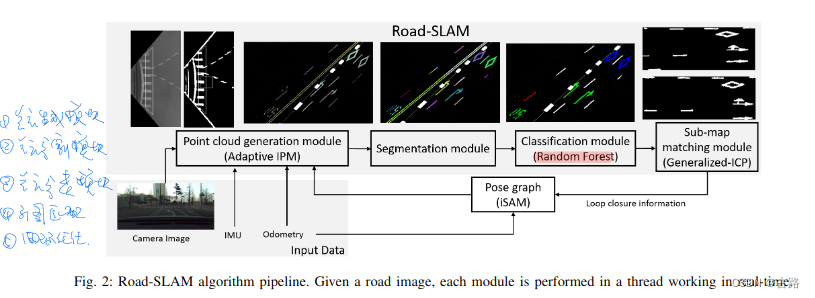
6.20220704_Road-SLAM : Road Marking based SLAM with Lane-level Accuracy

• 2017
• 基于Graph-SLAM，只使用了Road信息
• 子图思想进行回环检测
• 可以借鉴的算法：
  • 自适应IPM算法
  • 自适应二值化算法
  • 语义分类算法：通过形状函数集合（ESF）提取特征，然后使用随机森林进行分类
  • GICP算法进行匹配

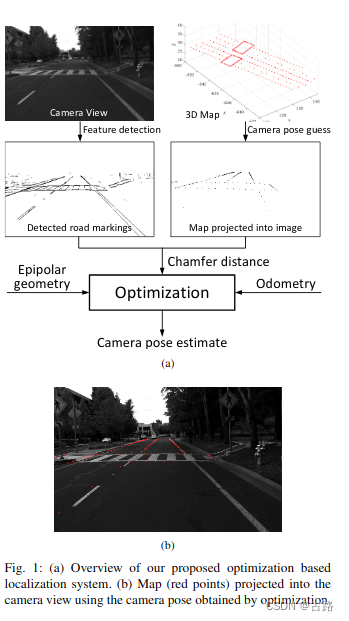
7.20220704_Monocular Localization in Urban Environments using Road Markings

• 2017
• 只有定位，没有建图，基于优化求解
• 地图使用的Lidar构建好的，使用单目进行定位
• 单目定位没有使用语义信息，使用道路边缘以及道路点的几何信息构建优化问题进行求解。
• edge提取：基于随机森林的边缘提取算法
• 匹配： Chamfer matching 算法

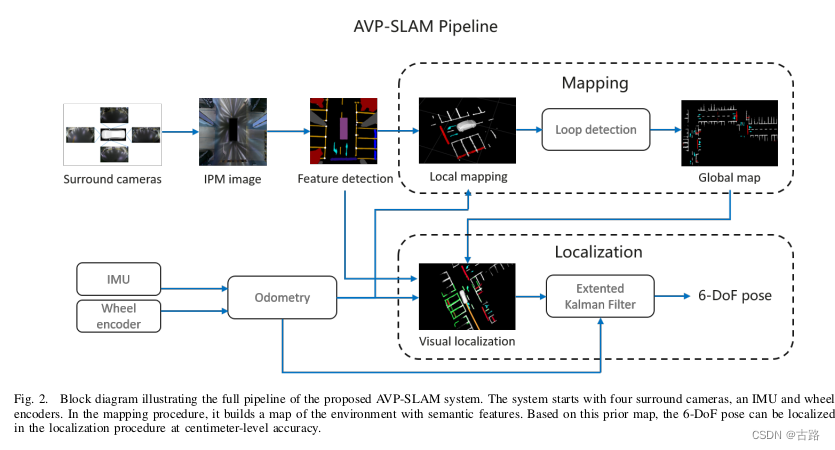
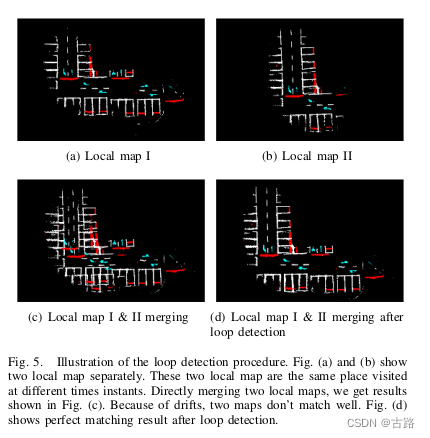
8.20220704_AVP-SLAM: Semantic Visual Mapping and Localization for Autonomous Vehicles in the Parking Lot

• 2020
• AVP-SLAM 作者秦通
• 环视 + IMU + 轮速计
• 环视 IPM 处理
• U-Net，对合成IPM图像的每一个像素输出一个标签，标签主要有lanes, parking lines, guide signs, speed bumps, free space, obstacles, and walls
• 建图（a）利用里程计进行局部建图,（b）ICP回环检测全局优化建图
• 定位（a）里程计定位，(b)语义ICP定位，EKF融合
• 主要贡献是提出方案框架
• AVP-SLAM:自主代客泊车视觉定位方案探索（自动驾驶）

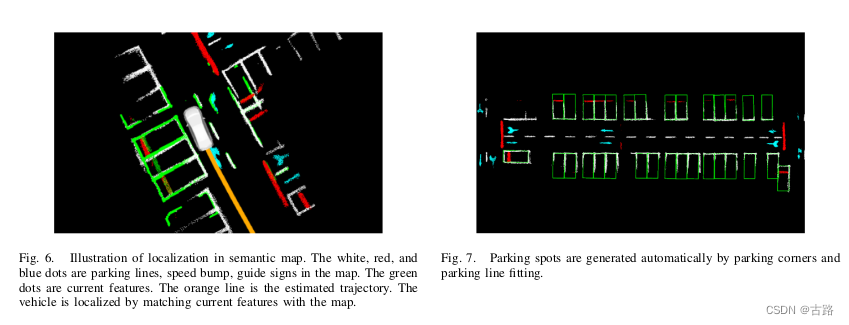
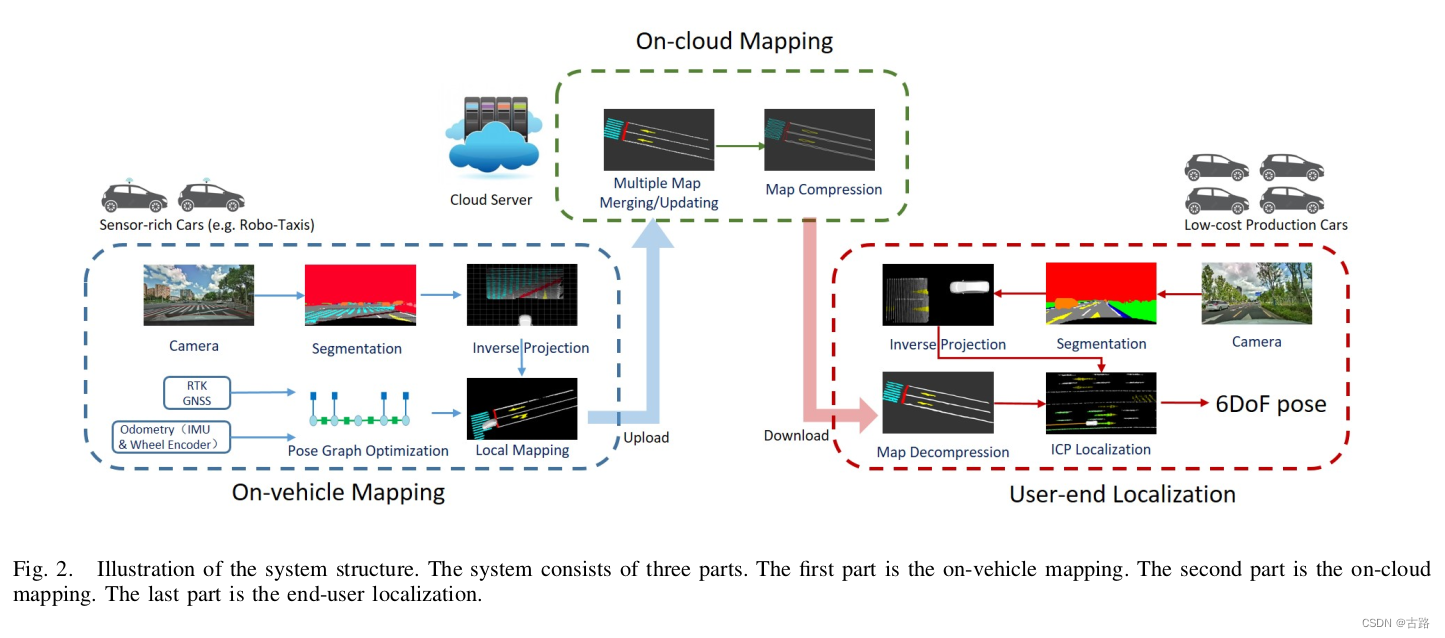
9.20220704_RoadMap: A Light-Weight Semantic Map for Visual Localization towards Autonomous Driving

• 2021
• RoadMap 作者秦通
• 车端建图（众包）、云端维护（融合、更新）、压缩(轮廓提取）分发
• 汽车本地建图：汽车使用前视照相机、RTK-GPS、IMU 和轮式编码器等传感器进行融合建图。其中 RTK-IMU 可以用来进行车辆位姿估计，相机图片可以用来提取语义特征，将提取到的语义特征投影至世界坐标系可以建立局部的语义地图。
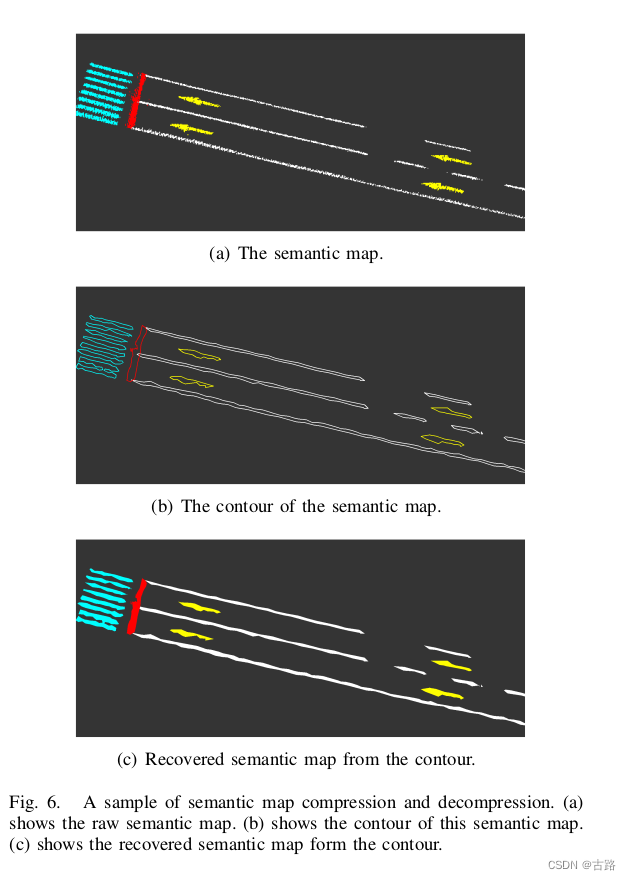
• 云端建图：汽车在本地建立的局部语义地图会上传至云端，云端服务器收集多个汽车的局部地图，通过拼接形成全局地图，然后对全局地图采用轮廓提取的方法进行压缩
• 用户端定位：用户可以实时获取最新的全局地图，只需要有低成本的相机、GPS、IMU 和编码器即可通过 GPS 和 IMU 进行粗定位，再结合语义信息匹配获取较为准确的位置估计
• 对云端数据进行一系列自动化的处理，便可以生产自动驾驶所使用的定位图层和拓扑图层,自动生成拓扑图层？
• 云端构图完成后，其他车辆经过该地图覆盖的区域后，便可以下载该轻量化的语义地图，进行导航和定位
• 定位和之前车端数据处理一样，提取前视相机的语义特征，通过和下载的语义地图比对，得到当前车辆的位姿
• 不用高精地图行不行？RoadMap：自动驾驶轻量化视觉众包地图
• 个人觉得可以以这篇文章为蓝本进行实现

10.20220704_Light-weight Localization for Vehicles using Road Markings

• 2013
• 本田
• 建图阶段：GPS+IMU+camera（检测 road mark）
• 定位阶段：通过 检测的 road mark 进行地图查询定位
• 创新点：更高特性的特征点检测
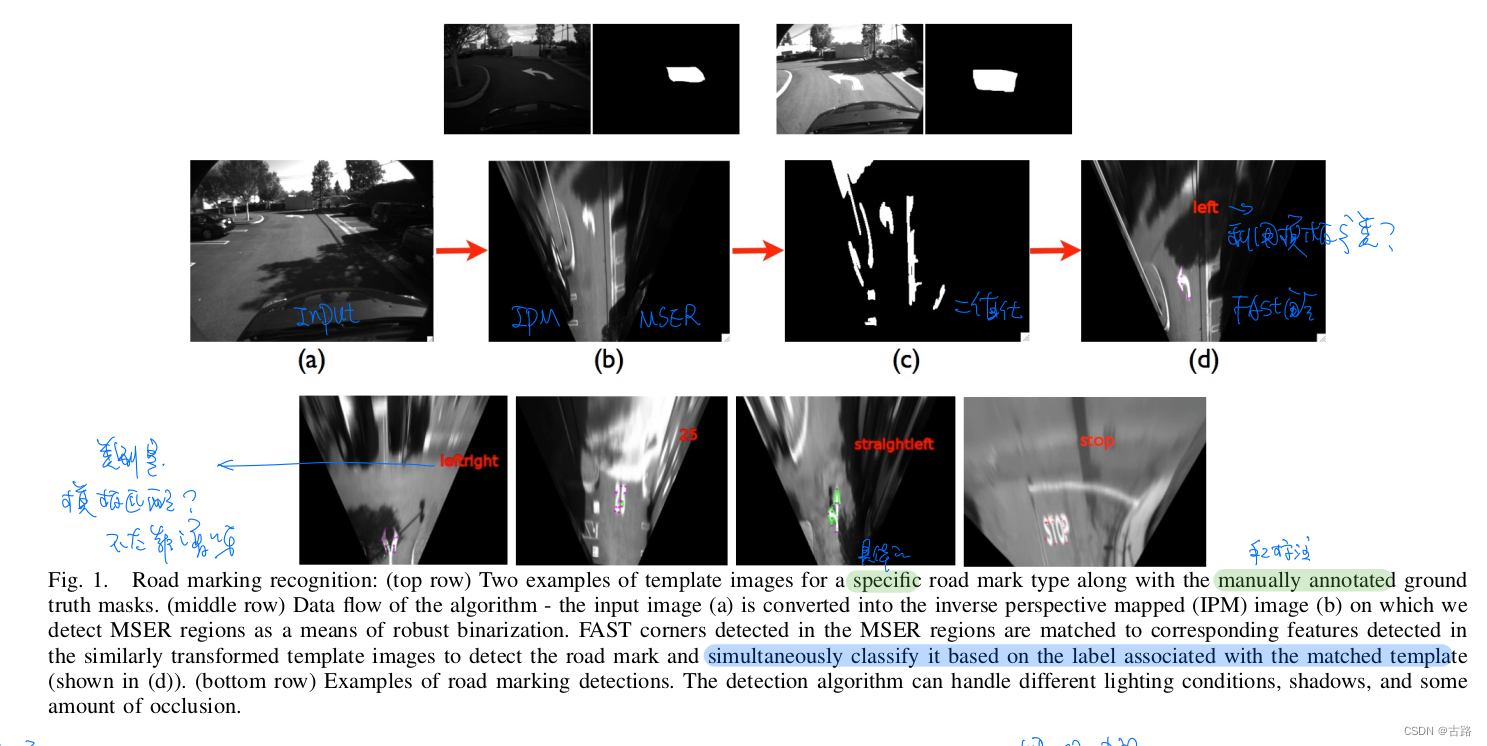
• we use MSER to find regions of interest that could potentially contain road markings
• IPM后，在 ROI 中提取 FAST 角点，使用 HOG 进行角点描述，并进行角点的标注
• We detect the contour of the road mark on the inverse perspective mapped (IPM) image using an active snake algorithm [8] and record the relative pixel locations of these corners within the contour.从角点点云中查找轮廓
• Road Mark是模板化的

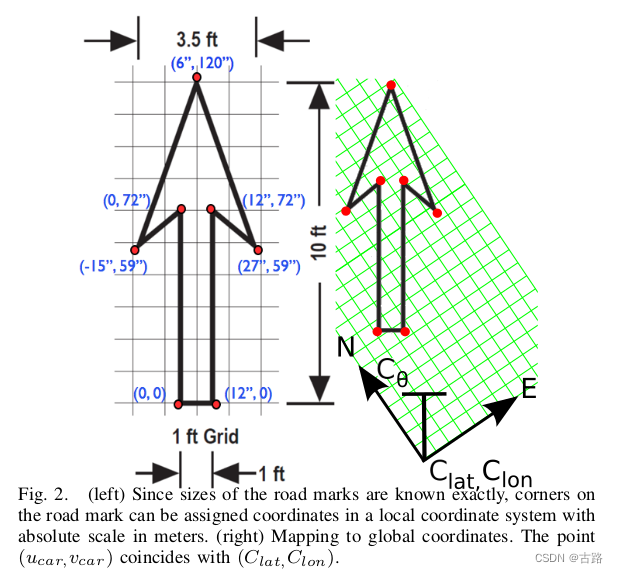
11.20220704_Submap-Based SLAM for Road Markings

• 2015
• 论文背景为一个大学生智能汽车竞赛
• 离线的SLAM过程
• ROI提取，IPM变换（selected a 2-D difference of Gaussian (DoG) as a filter 滤波畸变）特征提取算法为参考文献2
• 局部建图：占栅格地图，在线构建
• 全局优化：
• 感觉这篇文章没啥太突出的亮点啊，基本上是一些策略型的方法。

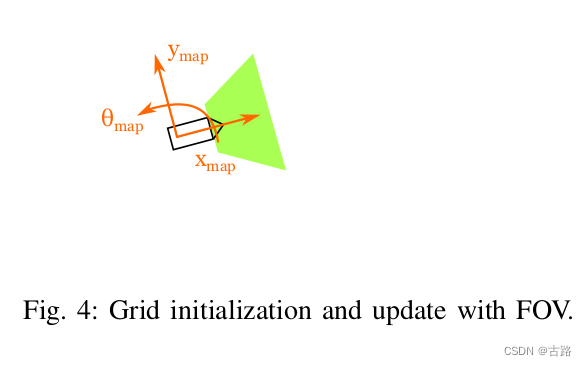
12.20220705_LaneLoc: Lane Marking based Localization using Highly Accurate Maps

• 2013
• 建图：360Lidar + 手工，就是传统的建图方式
• 文章主要工作在于已有地图后的定位，定位 = 横向定位 + 纵向定位
• 建图相机朝下安装，避免了 roll pitch 的影响
• 解读参考

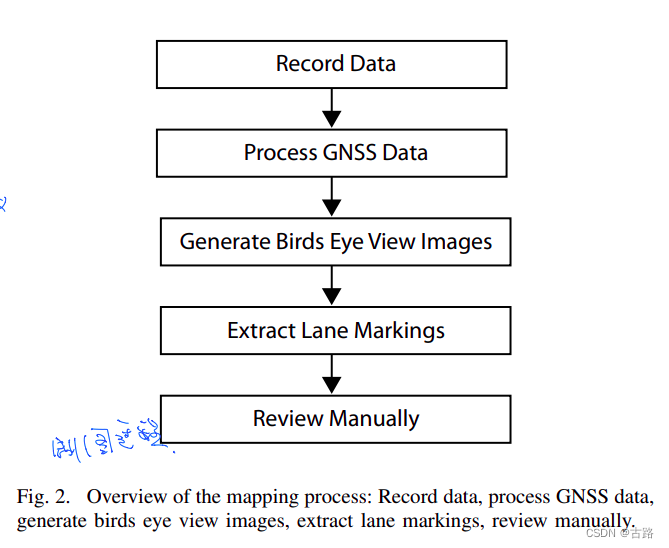
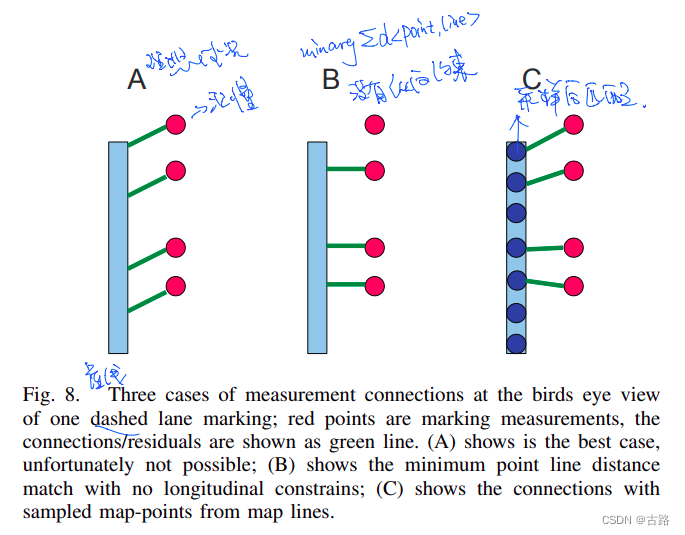
13.20220705_Lane marking aided vehicle localization

• 2013
• 采集车采集数据进行处理，具体怎么处理的没有详细展开
• 建图阶段：拿到lane points后：
  • Douglas–Peucker’s algorithm 降采样
  • 聚类
  • 最小二乘拟合参数得到lane模型(Each lane can have two border lines, both of them mapped into two polylines), Q:全是小线段组成的吗？
• 定位阶段：横向定位，纵向定位，很魔幻没咋看懂

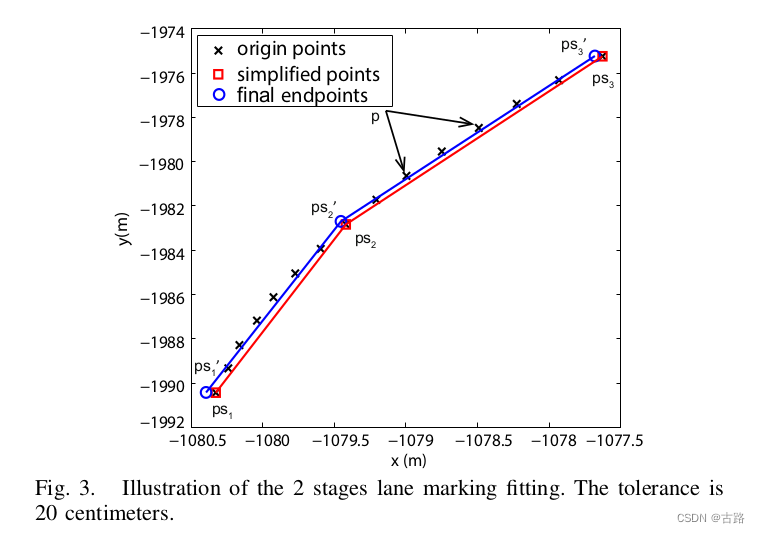
14.20220705_Visual Semantic Localization based on HD Map for Autonomous Vehicles in Urban Scenarios

• 2021

• 作者：华为诺亚方舟实验室

• 看华为的论文我似乎找到了他们写论文的固有格式：

  • 1.首页 = 摘要 + Introduction（由行业大方案，引出主要贡献）+ 一张漂亮图
  • 2.次页 = RELATED WORK（和本文类似的方案介绍，这里就很耐人寻味了，列出的参考文献，语句关键词都是来自与参考文献原文，简单变一下描述就是，很有可能就是来自于摘要） + 本系统框架图 + III.System overview
  • 3.后面依次为IV. METHODOLOGY + V. EXPERIMENTAL EVALUATION + VI. CONCLUSIONS + REFERENCES

• 传感器：单目相机(提取语义特征) + IMU + 两个编码器 + GNSS

• IV.METHODOLOGY

A. Semantic Features and Detection

• YOLOV3实现语义分割, sign–> $s_t=(s_t^l,s_t^c,s_t^b)$:
  • $s_t^l$: 点云类别
  • $s_t^c$:点云类别得分
  • $2_t^b$:类别boundingBox （四个顶点）
  • 加上相对当前位置的高度 height 一并存入到 HDMap 中
• pole–> $s_t=(s_t^l,s_t^c,s_t^b)$:
  • $s_t^l$: 点云类别
  • $s_t^c$:点云类别得分
  • $2_t^b$:类别 two vertices (端点)
  • 一并存入到 HDMap 中
• road marking： sample points 存入 HDMap 中

B. Semantic Data Association with HD map

step 1 在里程计先验位姿附近进行采样得到候选位姿（预测），并根据采样位姿将地图上的特征投影到图像上

• $p_i=\frac{1}{Z_i^c}K{T}_v^c{T}_v^{-1}{p}_i^m$；
• $p_i$: 地图中第 $i$ 个特征点位置
• $K,T_v^c$ 为相机内外参
• $Z_i^c$ 为地图中第 $i$ 个特征点在相机坐标系 $Z$ 轴的位置

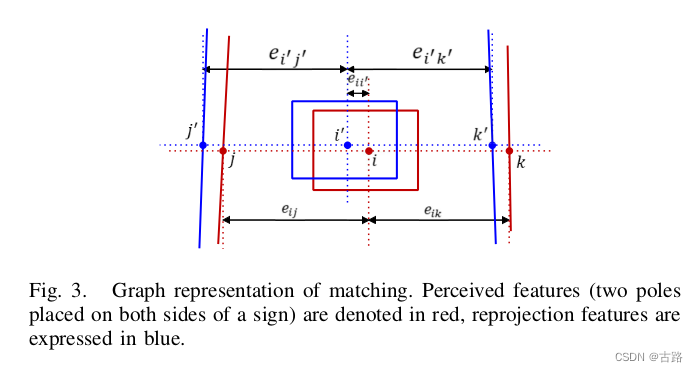
step 2 执行局部一致性的粗关联，找到近似最优的采样姿态，同时消除由于大的先验姿态误差引起的不匹配。 局部结构一致性：感知特征的横向位置分布 + 对应特征重投影最小化。（a）感知与重投影特征按横向位置升序排列； （b）计算每个感知特征 $s_t$ 和每个重投影特征 $r_k$ 之间的相似度:
$$p\left(s_t\mid r_k\right)=p\left(s_t^l\mid r_k^l\right)p\left(s_t^c\mid s_t^l,r_k^l\right)p\left(s_t^b\mid r_k^b\right)\text{\hspace{1em}(4)}$$
where, $p\left(s_t^l\mid r_k^l\right)$ and $p\left(s_t^c\mid s_t^l,r_k^l\right)$ can be obtained by offline learning of perception results.点云类别与点云得分相似度好计算

• For signs, the likelihood $p\left(s_t^b\mid r_k^b\right)$ consists of position and size similarity:这里就是计算 boundingBox的相似性
  p ( s t b ∣ r k b ) = ω exp ⁡ ( − 1 2 ( x p − u p σ p ) 2 ) + ( 1 − ω ) exp ⁡ ( − 1 2 ( x s − u s σ s ) 2 )
  p(stb∣rkb)=ωexp⁡(−12(xp−upσp)2)+(1−ω)exp⁡(−12(xs−usσs)2)" role="presentation">p(sbt∣rbk)=ωexp(−12(xp−upσp)2)+(1−ω)exp(−12(xs−usσs)2)$$\begin{array}{rl}p\left(s_t^b\mid r_k^b\right)=& \omega \exp \left(-\frac{1}{2}{\left(\frac{x_p-u_p}{{\sigma }_p}\right)}^2\right)+\\ & (1-\omega )\exp \left(-\frac{1}{2}{\left(\frac{x_s-u_s}{{\sigma }_s}\right)}^2\right)\end{array}$$
  p(stb​∣rkb​)=​ωexp(−21​(σp​xp​−up​​)2)+(1−ω)exp(−21​(σs​xs​−us​​)2)​
  ,
  • $\omega$ 是用于加权位置相似性和大小相似性的学习超参数。
  • $u_p、u_s、x_p、x_s$ 分别表示地图特征和感知特征的位置和大小。 ${\sigma }_p,{\sigma }_s$ 可以从感知结果中离线学习。
• 与 signs 相似，pole 的似然 $p(s_t^b|r_k^b)$ 由位置、方向和重叠相似性组成。
• 如果感知特征的最大相似度得分大于阈值并且保留了局部结构，则将它们视为匹配对。 对于每个采样姿势，计算cost $C$ 以根据匹配数 $N_m$ 和匹配误差 $e_{i{i}^{\prime }}$ 对其进行近似评估：
  $$C=-\frac{1}{N_m}\sum _{i=1}^{N_m}{e}_{i{i}^{\prime }}+\omega N_m$$
  $\omega$ is a hyperparameter. $e_{i{i}^{\prime }}$ is defined as the lateral distance between feature $i$ and $i^{\prime }$, as shown in Fig. 3. The proposal with $\max C$ is regarded as the approximate optimal matching sampled pose and will be used in step 3 .

step 3 基于 step2 中近似最优匹配采样位姿，进行考虑匹配数、匹配相似度和局部结构相似度的最优关联方法，实现最优全局一致性匹配。 通过解决以下优化问题，将其表述为多阶图匹配问题：

$$\begin{array}{rl}\hat{\mathbf{X}}=\underset{\mathbf{X}}{\mathrm{argmax}}{\omega }_1{N}_m+{\omega }_2\frac{1}{N_m}\sum _{i=1}^N\sum _{i^{\prime }=1}^M{x}_{i{i}^{\prime }}{s}_{i{i}^{\prime }}& \\ & +{\omega }_3\frac{1}{N_e}\sum _i^N\sum _{i^{\prime }}^M\sum _j^N\sum _{j^{\prime }}^M{x}_{i{i}^{\prime }}{x}_{j{j}^{\prime }}{s}_{ij,i^{\prime }{j}^{\prime }}\end{array}\text{\hspace{1em}(7)}$$
S.t.
$$\sum _{i=1}^N{x}_{i{i}^{\prime }}\le 1,\sum _{i^{\prime }=1}^M{x}_{i{i}^{\prime }}\le 1,x_{i{i}^{\prime }}=0\text{ or }1$$

• $N$ and $M$ are the number of perceived and reprojection features,
• $N_e$ is the number of edges between two features.
• ${\omega }_1,{\omega }_2$ and ${\omega }_3$ are hyperparameters.
• $x_{i{i}^{\prime }}$ denotes if perceived feature $i$ is matched with reprojection feature $i^{\prime }$.
• $s_{i{i}^{\prime }}$ represents the similarity between perceived feature $i$ and reprojection feature $i^{\prime }$, which is computed by equation (4). $s_{ij,i^{\prime }{j}^{\prime }}$ represents the similarity between edge $e_{ij}$ and $e_{i^{\prime }{j}^{\prime }}$ :
  $$s_{ij,i^{\prime }{j}^{\prime }}=\exp \left(-\frac{1}{2}{\left(\frac{e_{ij}-e_{i^{\prime }{j}^{\prime }}}{{\sigma }_e}\right)}^2\right)\text{\hspace{1em}(8)}$$
  • $e_{ij}$ and $e_{i^{\prime }{j}^{\prime }}$ denotes the lateral distance between feature $i$ and $j$, and feature $i^{\prime }$ and $j^{\prime }$, as shown in Fig. 3 .
  • ${\sigma }_e$ can be learned offline. The optimization problem will be solved by general random re-weighted walk framework [39].

step 4 执行连续帧间的特征跟踪。该过程在连续帧中的特征之间建立关联。 由于感知特征是静态的并保持局部结构，我们将该过程表述为类似于等式（7）的多阶图匹配问题。

step 5 执行时间平滑以得到时间一致性的数据关联。该过程在连续帧中的感知特征和地图特征之间构建最佳一致匹配。 当前帧的匹配正确性可以通过滑动窗口中先前的匹配结果来验证。 此外，如果当前帧中出现不匹配，则可以根据之前的匹配和跟踪来找到并纠正它。 时间平滑通过对滑动窗口中每一帧的匹配 $D_{1:T}$ 和匹配置信度 $c_{t,i}$ 加权来获取地图特征 $x^l$ 的对应感知特征 $s_i$：

$$\begin{array}{rl}{\hat{s}}_i& =\underset{s_i}{\mathrm{argmax}}p\left(s_i\mid D_{1:T}\right)\\ & =\underset{s_i}{\mathrm{argmax}}\frac{{\sum }_{t}I\left(s_i,D_t\right)c_{t,i}}{{\sum }_{t,j}I\left(s_j,D_t\right)c_{t,j}}\end{array}$$

• $I\left(s_i,D_t\right)$ denotes if map feature $x^l$ is matched with perceived feature $s_i$.

• The matching confidence $c_{t,i}$ is given by evaluating feature and local structure similarity:
  $$\begin{array}{rl}{c}_{t,i}& =\omega \exp \left(-\frac{1}{2}{\left(\frac{s_{i{i}^{\prime }}}{{\sigma }_p}\right)}^2\right)\\ & +(1-\omega )\exp \left(-\frac{1}{2}{\left(\frac{\frac{1}{N_m-1}{\sum }_{j=1,j\ne i}^{N_m}{s}_{ij,i^{\prime }{j}^{\prime }}}{{\sigma }_e}\right)}^2\right)\end{array}$$

• 如果最佳感知特征的累积置信度远大于次优感知特征的置信度，则认为最佳感知特征为地图特征$x^l$的匹配对。否则，认为地图特征$x^l$具有不确定匹配， 并且可以给出与每个感知特征的匹配概率。 该过程区分确定匹配和不确定匹配，可以解决奇点引起的不匹配问题。

C. Pose Graph Optimization

等式（2）的位姿估计过程可以定义为先验概率和似然的乘积：

$$\begin{array}{rl}\hat{\mathcal{X}}& =\underset{\mathcal{X}}{\mathrm{argmax}}p(\mathcal{X}\mid \mathcal{Z},\mathcal{L},\hat{\mathcal{D}})\\ & =\underset{\mathcal{X}}{\mathrm{argmax}}p(\mathcal{X})p(\mathcal{Z}\mid \mathcal{X},\mathcal{L},\hat{\mathcal{D}})\end{array}\text{\hspace{1em}(11)}$$

通过高斯分布假设，先验分布 $p(\mathcal{X})$ 是通过里程计的相对运动估计得到的。 我们基于里程计测量 $z_{i,i+1}^o$ 和匹配的特征对 $z_i^l$ 制定滑动窗口非线性最小二乘估计器，以估计最近的 $T$ 个姿势。 与常用的滤波方法相比，优化方法可以处理异步和延迟测量，并在相同的计算资源下实现更高的精度$[40]$。 优化目标表示为：

$$\begin{array}{rl}\hat{\mathcal{X}}=\underset{\mathcal{X}}{\mathrm{argmin}}& \sum _i{e}^o{\left(x_i^p,x_{i+1}^p,z_{i,i+1}^o\right)}^{\mathrm{T}}{\Omega }_i^o\\ & e^o\left(x_i^p,x_{i+1}^p,z_{i,i+1}^o\right)\\ & +\sum _i{e}^l{\left(x_i^p,x^l,z_i^l\right)}^{\mathrm{T}}{\Omega }_i^l{e}^l\left(x_i^p,x^l,z_i^l\right)\\ & +\sum _i{e}_j^m{\left(x^l\right)}^{\mathrm{T}}{\Omega }_j^m{e}_j^m\left(x^l\right))\end{array}\text{\hspace{1em}(12)}$$

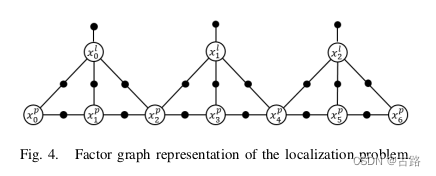
其中，每个误差项连同对应的信息矩阵可以看作一个因子，每个状态变量可以看作一个节点，因此定位问题可以用因子图表示，如图4所示。误差项由下式组成 里程计误差 $e^o$、语义测量误差 $e^l$ 和地图误差 $e_j^m$。 里程计误差定义为：

$$e^o\left(x_i^p,x_{i+1}^p,z_{i,i+1}^o\right)=\left(x_{i+1}^p{}^{\mathrm{T}}{x}_i^p\right)z_{i,i+1}^o$$
Semantic measurement error factor $e^l$ is expressed as:
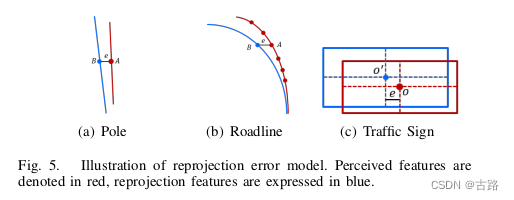
$$e^l\left(x_i^p,x^l,z_i^l\right)={\left[\frac{1}{Z_i^c}K{T}_v^c{x}_i^{p\mathrm{T}}{x}^l\right]}_0-{\left[z_i^l\right]}_0$$

其中，$[\cdot {]}_0$ 表示向量的第一个元素。 测量误差仅采用横向误差，以消除高度误差的影响以及对地图特征准确绝对高度的要求，如图5所示。

地图误差因子 $e_j^m$ 表示为：

$$e_j^m\left(x^l\right)=x^l-m_j$$

其中，$m_j$ 是第 $j$ 个地图特征的位置。 在本文中，我们采用参考文献[26]中提出的地图特征的方差构造方法。 在地图因子各向同性假设的情况下，根据假设的地图质量，地图因子的方差可以定义为：

$${\sigma }_m^2=\frac{1}{\gamma (c)}{r}^2$$

其中， $\gamma$ 是反卡方累积分布函数，$c$ 表示置信度，$r$ 表示半径。

非线性优化问题可以直接通过迭代算法求解。 采用滑动窗口代替全批处理方法，在保证定位精度的同时提高计算效率。 旧状态被直接截断和忽略。 边缘化方法也可以处理旧状态，但它会累积线性化误差，使系统矩阵密集，并导致死锁。 边缘化方法基于过去的数据约束姿态，但使用地图特征作为先验足以约束车辆姿态。

• 可能面临的问题:本文是以GPS组合导航提供绝对位姿，在定位的时候也是根据GPS提供搜索范围，在地下停车场中这是一个难点！

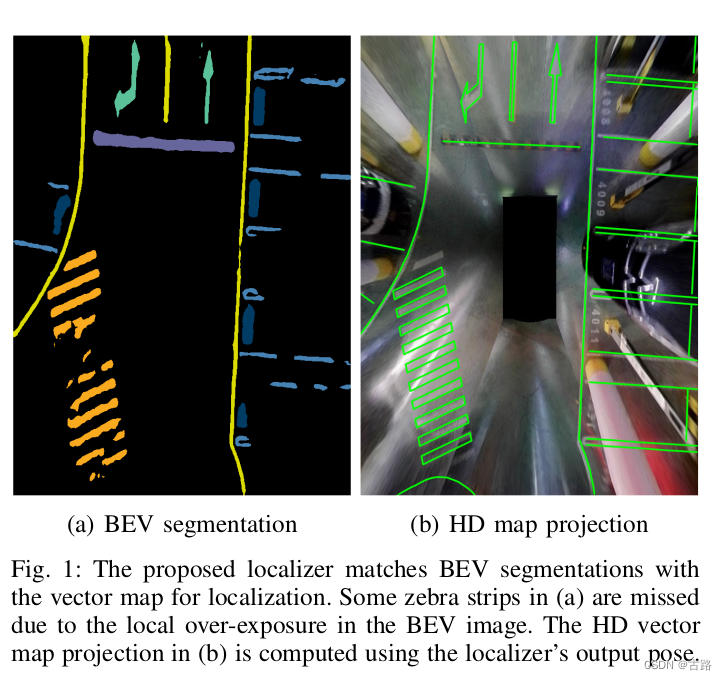
15.20220705_AVP-Loc: Surround View Localization and Relocalization Based on HD Vector Map for Automated Valet Parking

• 2021
• 作者：小米
• 文章剔除了利用 HD Vector Map 进行定位与重定位，并没有讨论 HDMap 是如何建立的；
• 提出来了 BEV语义图与 HDMap Vector Map 匹配的方案
• 提出来了利用HDMap vector Map进闭环检测的方案