-
C语言 数据的存储
一、数据与进制之间的关系
我们都知道,计算机存储的数据单位是二进制,要么是 0,要么是 1. 实际上,计算机就是用这种二进制序列来表示某个数值。
但我们也要理解与电子信息数据相关的其他表示方法:十进制、十六进制、八进制。因为在 C语言 中,常常需要用到将这些进制进行一定的转换。
十进制: (0 - 9) 二进制: (0 1) 八进制: (0 - 7) 十六进制: (0 - 9 a b c d e f)- 1
- 2
- 3
- 4
1. 十进制与二进制之间的转换
下图是数据为 11 的十进制与二进制之间的转换。此外,十进制与十六进制、十进制与八进制相互转换的过程也是同理。

2. 二进制与十六进制之间的转换
1 个字节 8 位 二进制,恰好可以用两个十六进制数据表示。

二、整型数据存储
1. 原、反、补码
计算机中的整数有三种表示方法,即原码、反码和补码。
三种表示方法均有符号位和数值位两部分。符号位 0 表示正,1 表示负;数值位就是正常的 0/1 序列。原码:直接将原数据按照正负数转换成二进制。
反码:原码的符号位不变,其他位依次按位取反。
补码:反码 +1.2. 整型数据在内存中的存储
int 类型的 10,与 int 类型的 -10 在内存中的存储如下:

从上面的图上看,我们可以得出结论:
① 整型数据存放内存中的是二进制补码。
② 正整数的原、反、补码是相同的;但负整数的原、反、补码则需要计算。
③ printf 格式化输出的是数据的原码。3. 为什么整型数据存在内存中存储的是补码
注意: CPU只有加法器,补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电路。这样一来,使用补码,则可以将符号位和数值域统一处理。
我们就拿 1 + (-1) = 0 来举例:
// 1 - 1 <==> 1 + (-1) 00000000 00000000 00000000 00000001 -> 1的原、反、补码 10000000 00000000 00000000 00000001 -> -1的原码 11111111 11111111 11111111 11111110 -> -1的反码 11111111 11111111 11111111 11111111 -> -1的补码- 1
- 2
- 3
- 4
- 5
- 6
- 7
// 错误的算法(使用原码相加) 00000000 00000000 00000000 00000001 -> 1的原码 + 10000000 00000000 00000000 00000001 -> -1的原码 10000000 00000000 00000000 00000010 -> 数值为 -2 // 正确的算法(使用补码相加) 00000000 00000000 00000000 00000001 -> 1的补码 + 11111111 11111111 11111111 11111111 -> -1的补码 100000000 00000000 00000000 00000000 -> 数值为 0(最前面的1 舍去)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
从结果来看,CPU 加法器对原码直接运算产生的结果是错误的,而采用补码是正确的。
4. 有符号和无符号的数据类型
char unsigned char signed char short <==> signed short // 有符号短整型 unsigned short // 无符号短整型 int <==> signed int // 有符号整型 unsigned int // 无符号整型 long <==> signed long // 有符号长整型 unsigned long // 无符号长整型- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
注意事项:
① unsigned 代表无符号类型,signed 代表有符号类型。如果没有特殊说明,一般就表示有符号类型。( 例如:int 就等价于 signed int 类型,即有符号整型。short、long 也默认为是有符号类型。但 char 官方并没有说明默认是有符号类型,这取决编译器的实现。)
② 有符号类型的二进制最高位是符号位,无符号类型的二进制最高位依然是数据位。
有符号和无符号的存储范围
我们以 char 类型的有符号和无符号对比, char 类型是一个字节,即 8 个比特位。

通过上图分析,我们可以看到有符号 char 类型的数据存储范围:-128 ~ 127,而 无符号 char 类型的数据存储范围:0 ~ 255. 类比 short、int、long 类型的数据范围也是这么计算来的。
猜想
理解了上面的有符号和无符号原理后,如果我们将一个负数放进一个无符号类型中,那么结果会发生什么事情呢?
程序清单:
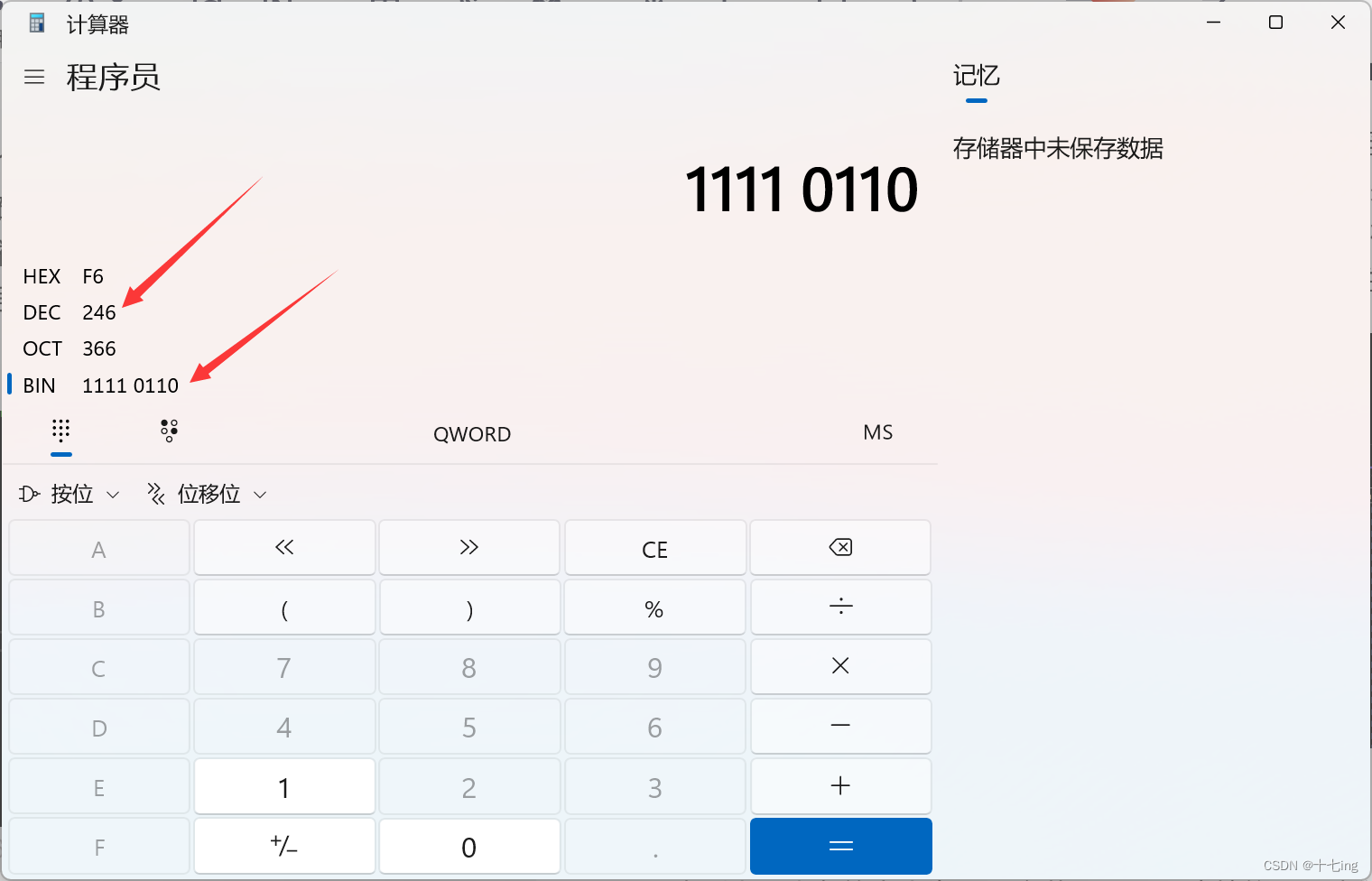
#includeint main() { unsigned char a = -10; printf("%u\n", a); // %u 为无符号打印 return 0; } // 输出结果:246 - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
从输出结果来看,-10 依然是按照二进制补码 11110110 存储至内存中的,只是在最后输出的时候,程序将 -10 的补码视为 -10 的原码直接就打印出来了,因为无符号整型本身就是一个不存在负数的类型,所以程序就视为原、反、补码相同才输出的。

所以输出结果并不是 -10,而是直接将其视为无符号二进制计算出的结果。
5. 关于 char 类型
char 类型占用内存的大小为 1 个字节,即 8 个比特位。而我们一般普遍认为 char 是字符类型。但实际上字符类型在底层存储字符的时候,存储却是字符对应的 ASCII 码值,所以我们依然可以将 char 类型视为整型。
字符 ’ A ’ 在内存中存储的二进制补码如下所示:实际上 ’ A ’ 的 ASCII 码值为 65,系统再转换成对应的二进制序列放入了内存中,为了方便显示,以十六进制显示在我们的面前。

三、大小端存储

在上图,我们可以看到局部变量 a,在内存中存储的是倒序的字节数据。这是为什么呢?其实这是在 VS 底下的编译器,它采用的是小端存储模式。
注意: 计算机在内存中存储数据是二进制序列,但是 VS 编译器为了方便我们观察,采用了十六进制显示序列 ( 2个十六进制位对应 8个二进制位,对应1个字节 )
1. 两种存储方式的区别
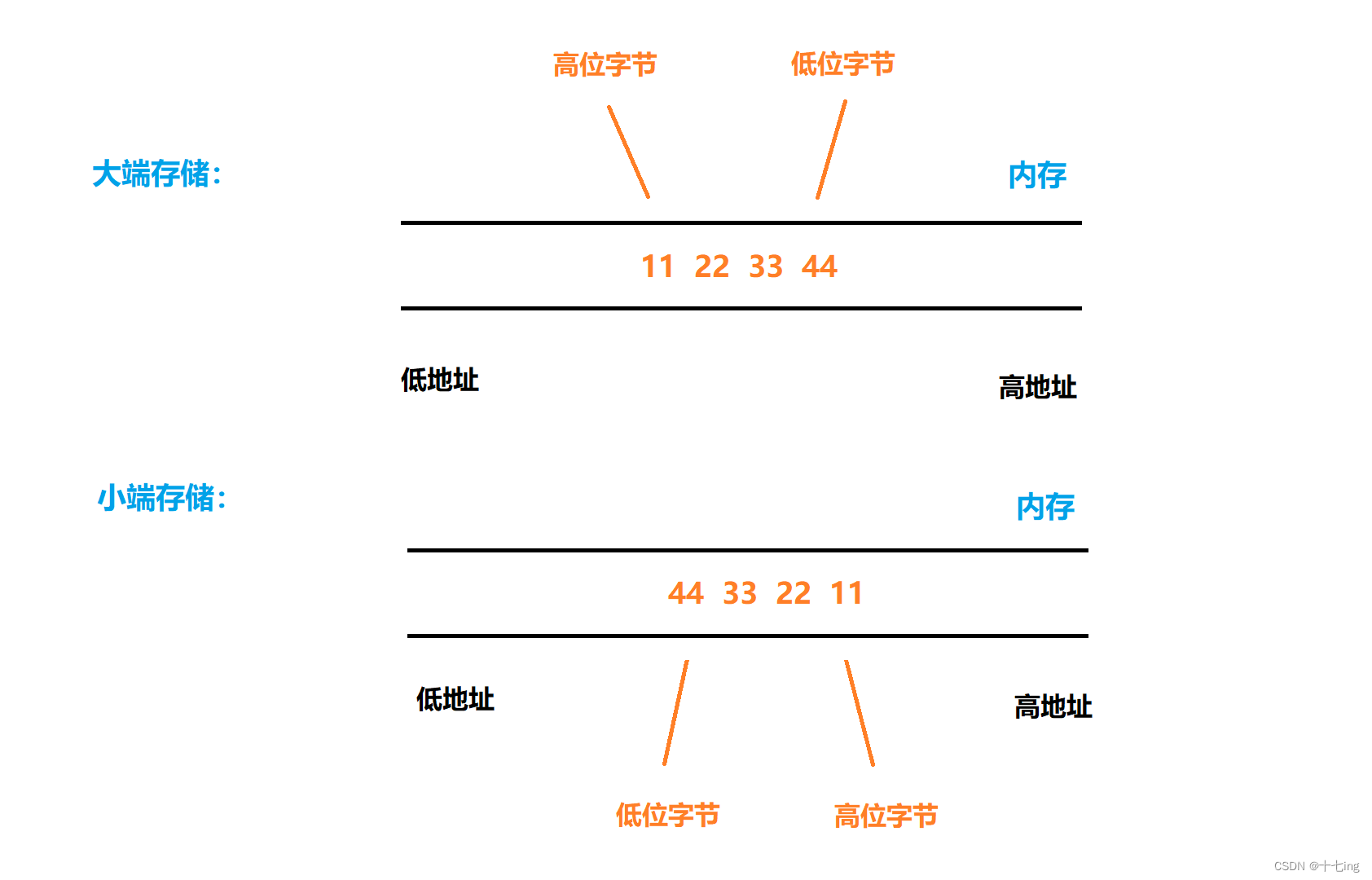
大端存储方式:数据的低位字节保存在内存的高地址中,而数据的高位字节保存在内存的低地址中。
小端存储方式:数据的低位字节保存在内存的低地址中,而数据的高位字节保存在内存的高地址中。
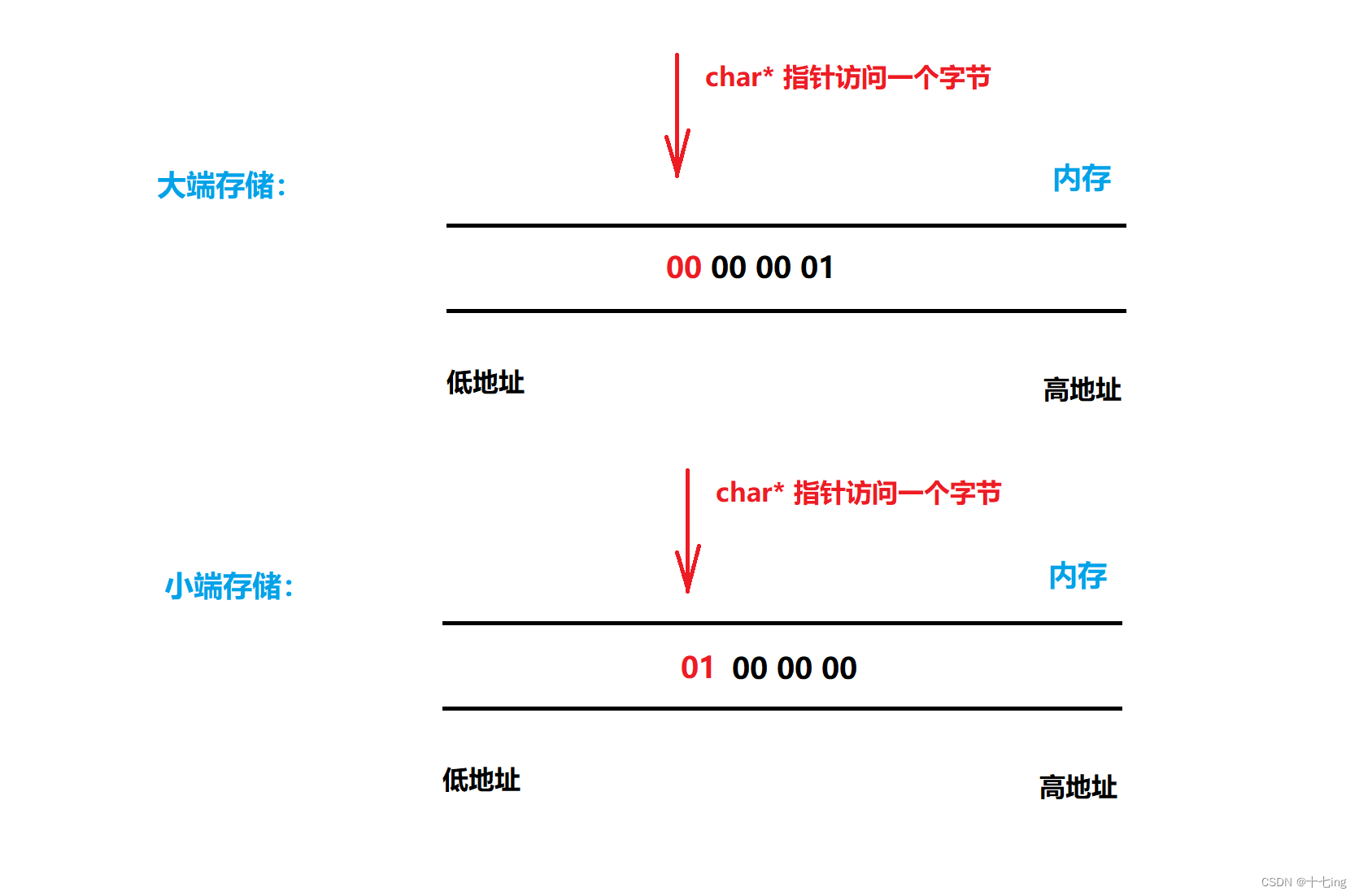
2. 设计一个程序来判断当前编译器的字节序存储
设计思路:利用 char* 指针来找到整个数据的第一个字节,从而判断是否为对应的字节值即可。( 例如:0x 00 00 00 01,如果是小端存储,必然第一个字节取出的是低位 01;反之如果是大端存储,必然第一个字节取出的是高位 00. )
注意: 利用指针访问、解引用都是从低地址往高地址操作的。
程序清单:
#includeint main() { int a = 0x00000001; char* p = (char*) & a; if (*p == 1) { printf("小端存储\n"); }else { printf("大端存储\n"); } return 0; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
四、整型提升
由于表达式的整型运算需要在 CPU 的相应运算器件内执行,而 CPU 内整型运算器(ALU) 的操作数的字节长度一般是 int 类型的字节长度,同时也是 CPU 的通用寄存器的长度。因此,即使两个 char 类型的变量相加,在 CPU 执行时也要先转换为 CPU 内整型操作数的标准长度。所以,表达式中各种长度可能小于 int 长度的整型值,都必须先转换为 int 或 unsigned int,然后才能送入 CPU 去执行运算。
注意:
① 对于有符号类型,整形提升是按二进制最高位补全。
② 对于无符号类型,整型提升直接按 0 补全。五、例题
程序清单1
#includeint main() { char a = -1; signed char b = -1; unsigned char c = -1; printf("a=%d, b=%d, c=%d", a, b, c); return 0; } // 输出结果:-1 -1 255 - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
运算过程:
① 变量 a 的运算过程 (变量 b 也是同理)
// 1. 将 -1 数据放入变量 a 的内存中 10000000 00000000 00000000 00000001 -> -1 原码 11111111 11111111 11111111 11111110 -> -1 反码 11111111 11111111 11111111 11111111 -> -1 补码 11111111 // 截断成 char 类型,放入变量 a 中(补码) // 2. 整型提升,由于变量 a 是有符号类型,所以按最高位补全 11111111 11111111 11111111 11111111 -> 新的补码 // 3. %d 打印,输出一个有符号的整型数据 11111111 11111111 11111111 11111111 -> 新的补码 11111111 11111111 11111111 11111110 -> 新的反码 10000000 00000000 00000000 00000001 -> 新的原码 (最终输出 -1)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
② 变量 c 的运算过程
// 1. 将 -1 数据放入变量 c 的内存中 10000000 00000000 00000000 00000001 -> -1 原码 11111111 11111111 11111111 11111110 -> -1 反码 11111111 11111111 11111111 11111111 -> -1 补码 11111111 // 截断成 char 类型,放入变量 c 中(补码) // 2. 整型提升,由于变量 c 是无符号类型,所以按 0 补全 00000000 00000000 00000000 11111111 -> 新的原、反、补码 // 3. %u 打印,输出一个无符号的整型数据 00000000 00000000 00000000 11111111 -> 不存在负数,直接输出 255- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
程序清单2
#includeint main() { char a = 3; char b = 127; char c = a + b; printf("%d\n", c); return 0; } // 输出结果:-126 - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
计算过程:
// 1. 将 a + b 的结果数据放入变量 c 的内存中 00000000 00000000 00000000 00000011 -> 3 的原、反、补码 00000011 // 截断成 char 类型,放入变量 a 中(补码) 00000000 00000000 00000000 01111111 -> 127 的原、反、补码 01111111 // 截断成 char 类型,放入变量 b 中(补码) // 2. 整型提升,由于变量 a, b 是有符号类型,所以按最高位补全 00000000 00000000 00000000 00000011 -> 3 的补码 + 00000000 00000000 00000000 01111111 -> 127 的补码 = 00000000 00000000 00000000 10000010 -> 新的补码 10000010 // a + b 的结果,截断成 char 类型,放入变量 c 中(补码) // 3. 整型提升,由于变量 c 是有符号类型,所以按最高位补全 11111111 11111111 11111111 10000010 -> 新的补码 // 4. %d 打印,输出一个有符号的整型数据 11111111 11111111 11111111 10000010 -> 新的补码 11111111 11111111 11111111 10000001 -> 新的反码 10000000 00000000 00000000 01111110 -> 新的原码 (最终输出 -126)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
程序清单3
#includeint main() { char a = -128; char b = 128; printf("%u %u\n", a, b); return 0; } // 输出结果:4294967168 4294967168 - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
运算过程:变量 a
// 1. 将 -128 数据放入变量 a 的内存中 10000000 00000000 00000000 10000000 -> -128 原码 11111111 11111111 11111111 01111111 -> -128 反码 11111111 11111111 11111111 10000000 -> -128 补码 10000000 // 截断成 char 类型,放入变量 a 中(补码) // 2. 整型提升,由于变量 a 是有符号类型,所以按最高位补全 11111111 11111111 11111111 10000000 // 3. %u 打印,输出一个无符号的整型数据 11111111 11111111 11111111 10000000 -> 不存在负数,直接输出 4294967168- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
运算过程:变量 b
// 1. 将 128 数据放入变量 b 的内存中 00000000 00000000 00000000 10000000 -> 128 原、反、补码 10000000 //截断成 char 类型,放入变量 b 中(补码) // 2. 整型提升,由于变量 b 是有符号类型,所以按最高位补全 11111111 11111111 11111111 10000000 -> 新的补码 // 3. %u 打印,输出一个无符号的整型数据 11111111 11111111 11111111 10000000 -> 不存在负数,直接输出 4294967168- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
程序清单4
#includeint main() { int i = -20; unsigned int j = 10; printf("%d\n", i + j); return 0; } // 输出结果:-10 - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
运算过程:
10000000 00000000 00000000 00010100 -> -20 原码 11111111 11111111 11111111 11101011 -> -20 反码 11111111 11111111 11111111 11101100 -> -20 补码 00000000 00000000 00000000 00001010 -> 10 原、反、补码 // 1. i + j 的计算过程 11111111 11111111 11111111 11101100 -> -20 补码 + 00000000 00000000 00000000 00001010 -> 10 补码 = 11111111 11111111 11111111 11110110 -> 新的补码 // 2. %d 打印,输出一个有符号的整型数据 11111111 11111111 11111111 11110110 -> 新的补码 11111111 11111111 11111111 11110101 -> 新的反码 10000000 00000000 00000000 00001010 -> 新的原码 (最终输出 -10)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
程序清单5
#include#include int main() { unsigned int i; for (i = 9; i >= 0; i--) { printf("%u\n", i); Sleep(1000); // 休眠 1 秒 } return 0; } // 输出结果:9 8 7 6 5 4 3 2 1 0 4294967295 4294967294... - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
运算过程:
00000000 00000000 00000000 00001001 -> 9 的原、反、补码 ... 10000000 00000000 00000000 00000001 -> - 1 原码 11111111 11111111 11111111 11111110 -> - 1 反码 11111111 11111111 11111111 11111111 -> - 1 补码 (4,294,967,295) // 当 -1 放入无符号变量 i 中时,此时程序就不将其视为负数了, // 所以最终将其视为无符号直接输出,即所有的二进制补码序列全是数据位- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
程序清单6
#include#include int main() { char a[1000]; int i; for (i = 0; i < 1000; i++) { a[i] = -1 - i; } printf("%d\n", strlen(a)); return 0; } // 输出结果:255 - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
首先,我们得明白 strlen 是用来求字符串的长度的 ( ’ \0 ’ 之前的),而 ’ \0 ’ 的 ASCII 码也是 0. 所以对于上面的程序,当字符数组中间的元素出现 字符0 时, 就意味着 strlen 函数计算字符串长度已经到头了。
计算过程:
截断发生的过程:
// i = 0 10000000 00000000 00000000 00000001 -> -1 原码 11111111 11111111 11111111 11111110 -> -1 反码 11111111 11111111 11111111 11111111 -> -1 补码 11111111 // 截断放入 a[0] 中(补码) // i = 1 10000000 00000000 00000000 00000010 -> -2 原码 11111111 11111111 11111111 11111101 -> -2 反码 11111111 11111111 11111111 11111110 -> -2 补码 11111110 // 截断放入 a[1] 中(补码) // i = 2 10000000 00000000 00000000 00000011 -> -3 原码 11111111 11111111 11111111 11111100 -> -3 反码 11111111 11111111 11111111 11111101 -> -3 补码 11111101 // 截断放入 a[2] 中(补码) ... ...- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
经过上面的分析,可以总结出,字符数组中第 256 位被放入的是 0,所以在第 256 位之前,就是应该 strlen 所计算的字符串长度,即 255.
(从 00000000 到 11111111 总共有 2^8 种情况,即 256.)
// 字符数组中每个字符存储的二进制补码 11111111 -> -1 补码 11111110 -> -2 补码 11111101 -> -3 补码 ... ... 00000001 00000000 // 第 256 位补码- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
或者我们也可以如下分析:
无符号的 char 类型的范围:-128 ~ 127

程序清单7
#include#include unsigned char i = 0; int main() { for (i = 0; i <= 255; i++) { printf("hello world, %d\n", i); Sleep(100); // 休眠 0.1 秒 } return 0; } // 输出结果:(死循环) 0 - 255, 0 - 255, 0 - 255 ... - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
运算过程:
有符号的 char 类型的范围:0 ~ 255
00000000 -> 0 补码 00000001 -> 1 补码 ... ... 11111111 -> 255 补码 100000000 -> 256 补码 -> 截断成 00000000 00000001 -> 1 补码 ... ...- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
-
相关阅读:
OpenCV4之特征提取与对象检测
离散数学---判断矩阵:自反性,反自反性,对称性得到矩阵的自反闭包,对称闭包。
不受约束的bimap双图的测试程序
NOI2022 游记
讲解器厂家深层互联重磅发布行业首个头戴式无线讲解器
阿里直呼真省钱!全网首发IntelliJ IDEA应用实战手册竟遭哄抢
Vue2封装评论组件详细讲解
计算机网络_04_传输层
【Redis】谈谈我对Redis布隆过滤器的理解
计算机组成原理---第三章存储系统---主存储器和CPU的连接
- 原文地址:https://blog.csdn.net/lfm1010123/article/details/127884865