• 第三章：高精度算法（加、减、乘、除）

    高精度算法

    高精度的整体思路：

    为什么一个数据会存在最大数？我们知道，一个数字会转化成二进制存储在内存中。而每个二进制位都会消耗一个比特位。我们以int 为例，其大小是4个字节，32个比特位。因此，其所表示的最大数即32个比特位全是1的时候。

    因此，我们只要打破内存的限制，就能实现超级大的数字之间的加减乘除运算。那么如何打破呢？此时我们就需要用到我们学过的数组，我们的数组可以在相应的内存区域限制内不断地开辟，从而满足我们的需要。

    因此高精度的本质就是利用数组模拟各种运算法则，从而得到结果。

    一、加法

    1、思路：

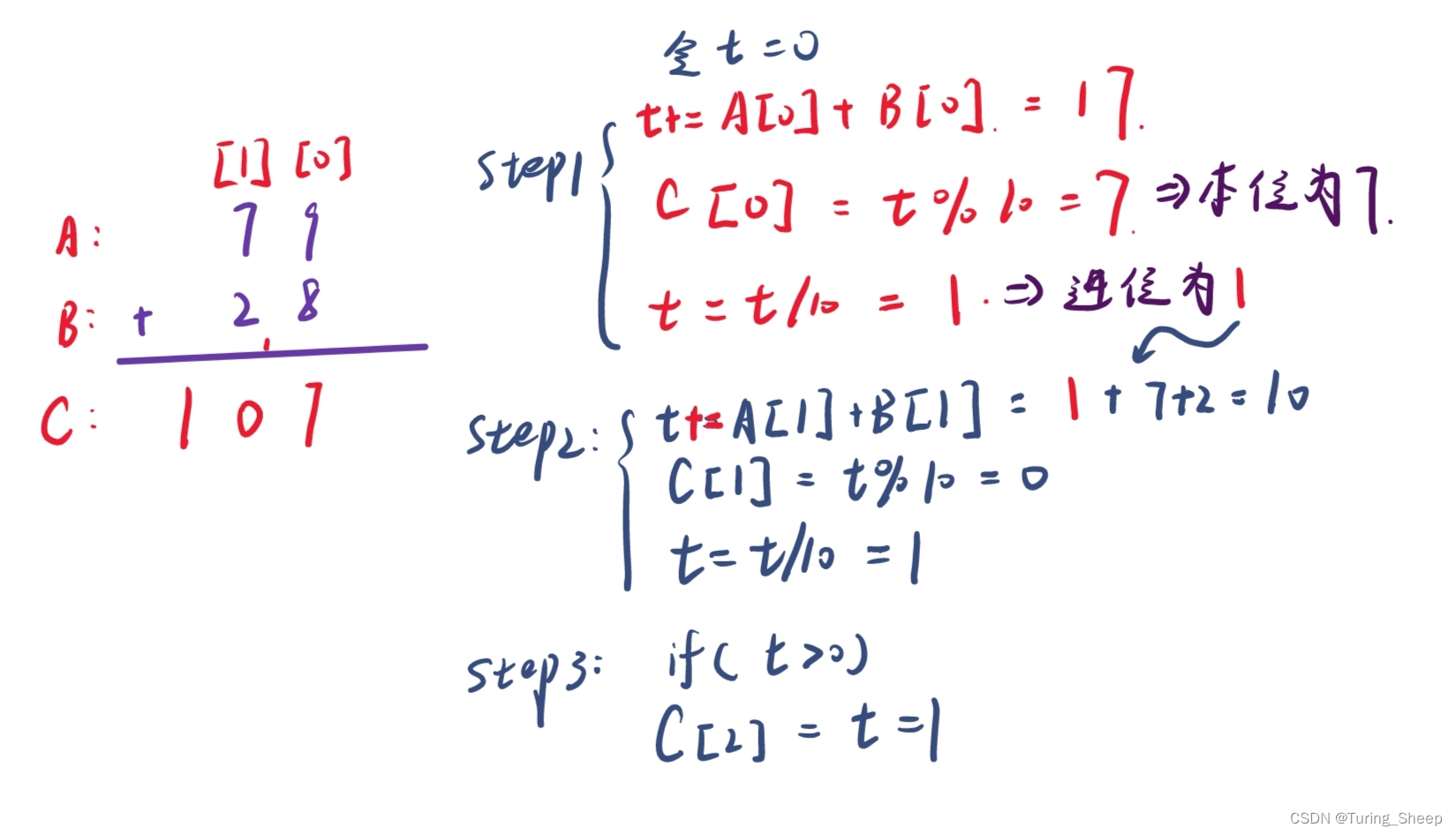
    在这里插入图片描述
    我们以上述图示为例子，我们创建两个数组，模拟两个数字的位数，从个位开始运算。

    我们创建一个中间变量t来存储每一位两个数字加起来的结果。但是我们需要注意的是，结果中的每一位不仅来自A,B两个数字中对应位数的相加，还包括前一位的进位。

    个位的加减是没有前一位的进位的，因此我们初始化 t 为0。然后运算结果如上图所示。我们将t%10后，就是该位所应保留的数字，然后将t在/=10，此时t就保留了进到下一位中的进位。

    因此，我们这里要写成：t += A[i] + B[i]。一定是+=!!。否则就会丢掉进位。不懂得话，可以详细看上面图片中的手写例子。

    但是我们还需要注意的一点就是，当我们算到最后一位的时候，最后一位计算结束的时候，我们的t有可能依然有进位。由于A，B已经没有下一位了。所以如果不特殊处理以下的话，这一位就丢掉了。因此我们用if语句判断一下，如果存有进位，则再开一位存储1。

    另外的一些细节，我们看完模板再解释。

    2、模板：

    （1）C++版：

    #include
#include
#include
using namespace std;
vector<int>add(vector<int>&A,vector<int>&B)
{
	int t=0;
	vector<int>C;
	for(int i=0;i<A.size()||i<B.size();i++)
	{
		if(i<A.size())t+=A[i];
		if(i<B.size())t+=B[i];
		C.push_back(t%10);
		t/=10;
	}
	if(t!=0)C.push_back(1);
	return C;
}
int main()
{
	string a,b;
	vector<int>A,B;
	cin>>a>>b;
	//倒序存储数组
	for(int i=a.size()-1;i>=0;i--)A.push_back(a[i]-'0');
	for(int i=b.size()-1;i>=0;i--)B.push_back(b[i]-'0');
	//调用加法函数
	vector<int>C=add(A,B);
	//倒序输出结果
	for(int i=C.size()-1;i>=0;i--)printf("%d",C[i]);
	return 0;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32

    （2）C语言版：

    #include
#include
char a[100005];
char b[100005];
int A[100005];
int B[100005];
int C[100005];

int main()
{
    scanf("%s",a);
    scanf("%s",b);
    int lena = strlen(a);
    int lenb = strlen(b);
	//逆序数组
    for (int i = 0; i < lena;i++)
    {
        A[lena - i - 1] = a[i] - '0';
    }

    for (int i = 0; i < lenb;i++)
    {
         B[lenb - i - 1] = b[i] - '0';
    }
  
	//判断结果的最大位数
    int lenc = (lena > lenb ? lena : lenb)+1;
	//开始加法
	int t=0;
	int i;
    for (i = 0; i < lenc;i++)
    {
    	t+=A[i]+B[i];
    	C[i]=t%10;
    	t/=10;
    }
    if(t!=0)C[i]=1;
    
    //删除前导零，避免出现：000012的情况。但是要注意0这种特殊情况
    while(C[lenc]==0&&lenc>0)
    {
         lenc--;
    }
	
    for (int i = lenc; i >= 0;i--)
    {
         printf("%d",C[i]);
    }

         return 0;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51

    我们这里解释一下为什么要倒置数组，因为我们输入一个字符串后，第一个元素是最高位。但是我们上述图片举得例子中，第一个元素是个位，所以我们需要倒置数组，不要忘记剪掉：'0'
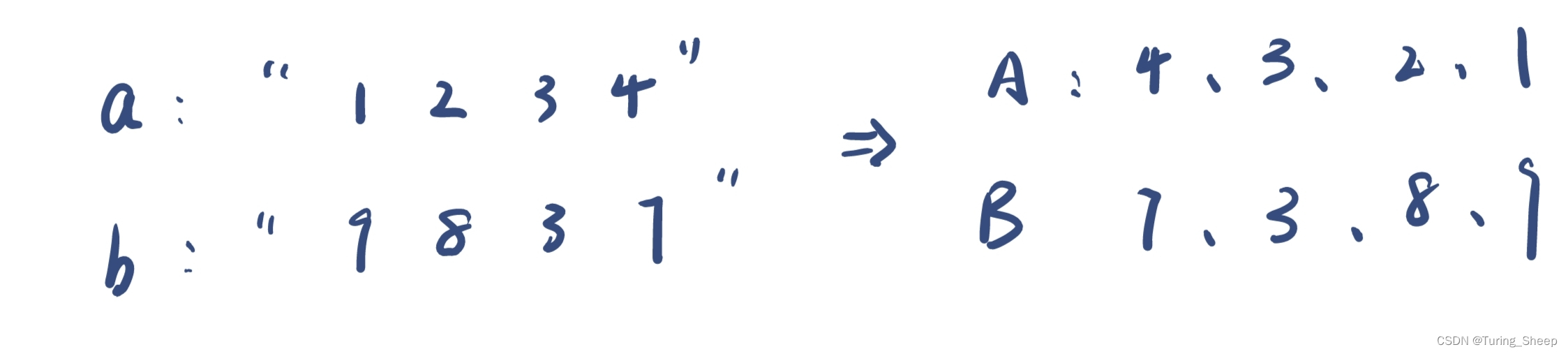
    在这里插入图片描述

    二、减法

    1、思路：

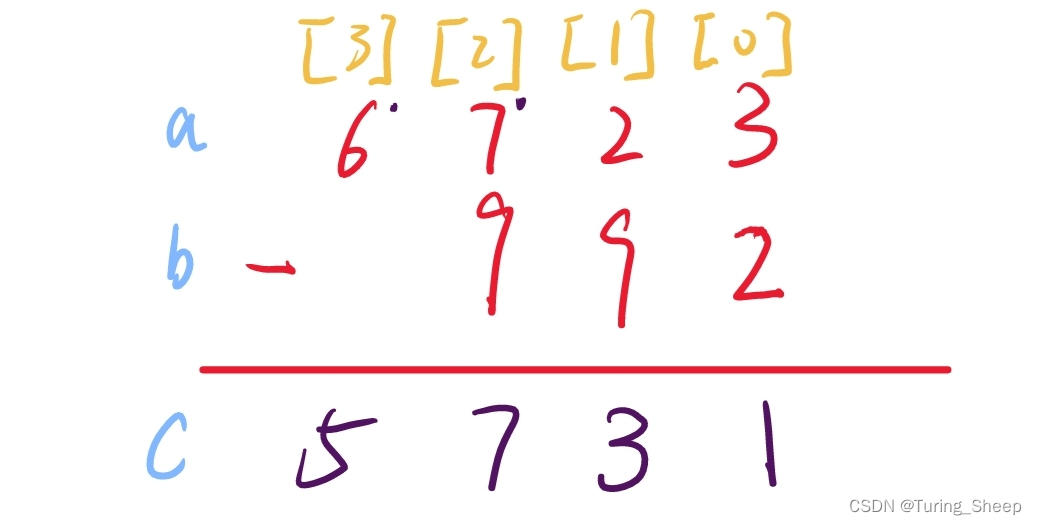
    请添加图片描述
    减法依旧是去模拟一个竖式的计算，上面的图片中就是我们小学数学中所熟悉的式子。那么我们从编程的角度去审视一下上面的代码：
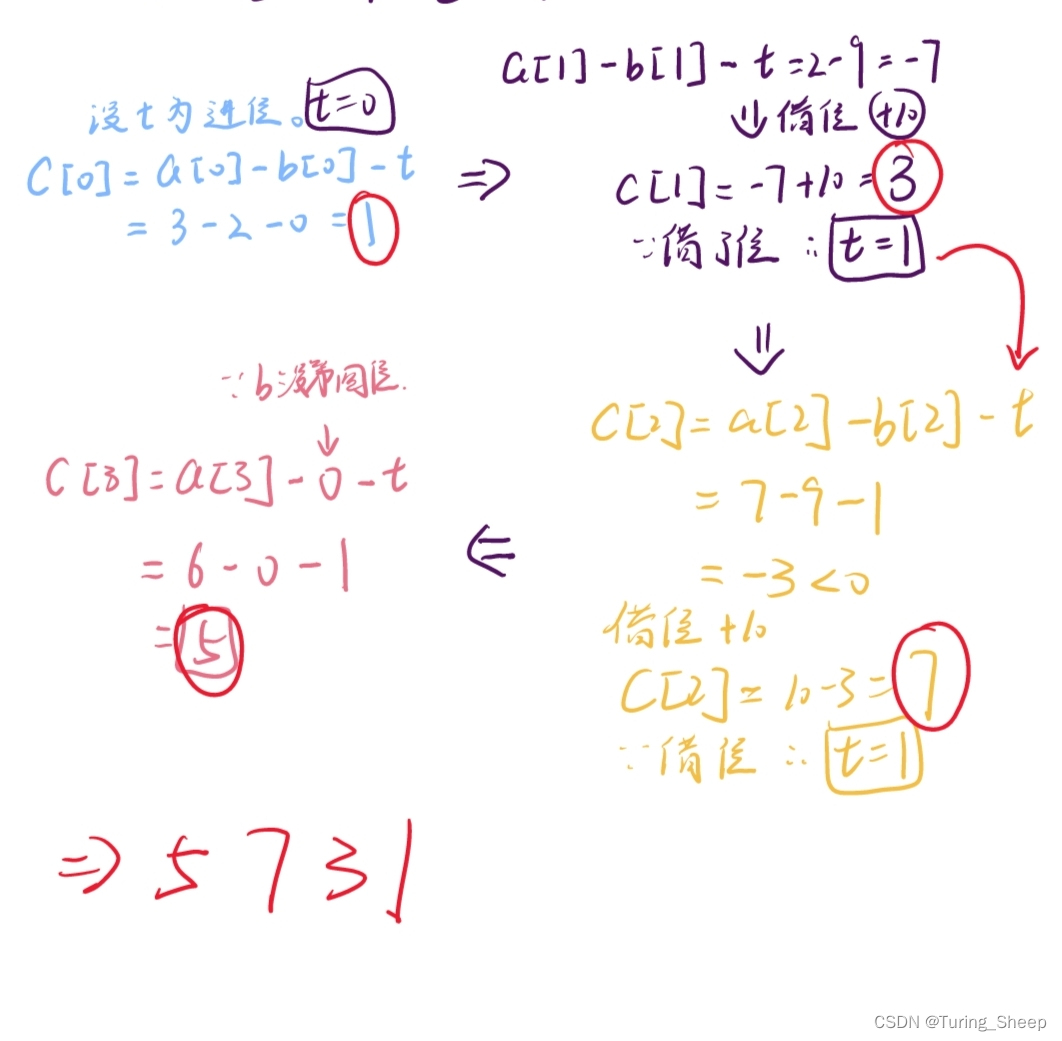
    请添加图片描述
    通过上面的代码，我们可以总结出减法中的关键思路：
    创建一个临时变量t,这个t就是辅助我们去计算每一位的。那么这个t代表的是进位。同时我们也利用t来存储每一位运算的结果，然后再通过对t的取模运算得到每一位的结果，然后再通过A[i]-B[i]-t的正负去判断进位。
    这里我们解释一下，当A[i]-B[i]小于0的时候，说明我们是需要借位的，借位其实就是给这个负数的结果加上一个10，因为我们借位了，所以t要等于1。所以在下一位的计算过程中，我们就要多减去一个1,那么多减去的这个1就体现在 - t 中。

    当我们的结果是负数的时候，我们还需要去模拟那个负数，因此我们需要先判断一下正负，然后预先得知是否打印负号，然后我们再去求二者相减的绝对值即可。

    接着下来的话，我们需要还需要解决一下前导零的问题：比如777-772=005。5之前的00是没必要打印的，我们直接删除即可。

    2、模板：

    C++

    #include
#include
using namespace std;
bool cmp(vector<int>&A,vector<int>&B)
{
    if(A.size()!=B.size())return A.size()>B.size();
    else
    {
        for(int i=A.size()-1;i>=0;i--)
        {
            if(A[i]!=B[i])return A[i]>B[i];
        }
    }
    return true;
}
vector<int>sub(vector<int>&A,vector<int>&B)
{
    vector<int>C;
    int t=0;
    for(int i=0;i<A.size();i++)
    {
        t=A[i]-t;
        if(i<B.size())t-=B[i];
        if(t>=0)
        {
            C.push_back(t);
            t=0;
        }
        else
        {
            C.push_back(t+10);
            t=1;
        }
    }
    while(C.size()>1&&C.back()==0)C.pop_back();
    return C;
}
int main()
{
    vector<int>A,B,C;
    string a,b;
    cin>>a>>b;
    for(int i=a.size()-1;i>=0;i--)A.push_back(a[i]-'0');
    for(int i=b.size()-1;i>=0;i--)B.push_back(b[i]-'0');
    if(cmp(A,B))
    {
        C=sub(A,B);
    }
    else
    {
        C=sub(B,A);
        cout<<"-";
    }
    for(int i=C.size()-1;i>=0;i--)printf("%d",C[i]);
    return 0;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56

    C

    #include
#include

char a[100010],b[100010];
int A[100010],B[100010],C[100010];

int cmp(int*A,int*B,int lena,int lenb)
{
    int len=lena-lenb;
    if(len!=0)
    {
        return len;
    }
    else
    {
        for(int i=lena-1;i>=0;i--)
        {
            if(A[i]!=B[i])
            {
                return A[i]-B[i];
            }
        }
    }
    return 0;
}

int sub(int*A,int*B,int*C,int lena,int lenb)
{
    int t=0,lenc=0;
    for(int i=0;i<lena;i++)
    {
        t=A[i]-t;
        
        if(i<lenb)t-=B[i];
        
        if(t>=0)
        {
            C[i]=t;
            t=0;
        }
        else
        {
            C[i]=t+10;
            t=1;
        }
        lenc++;
    }
    while(lenc>1&&C[lenc-1]==0)lenc--;
    return lenc;
}

int main()
{
    scanf("%s %s",a,b);
    int lena=strlen(a);
    int lenb=strlen(b);
    int lenC=0;
    for(int i=0;i<lena;i++)A[i] = a[lena - i - 1] - '0';
    for(int i=0;i<lenb;i++)B[i]=b[lenb-i-1]-'0';
    
    if(cmp(A,B,lena,lenb)>=0)
    {
        lenC=sub(A,B,C,lena,lenb);
    }
    else
    {
        lenC=sub(B,A,C,lenb,lena);
        printf("-");
    }
    for(int i=lenC-1;i>=0;i--)printf("%d",C[i]);
	return 0;
}


    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73

    三、乘法

    1、思路：

    我们这里的乘法介绍的是一个较小的数乘以一个大整数，即只把大整数存储到数组中，而这个较小的数字依旧存储在一个整型当中。思路如下所示：
    在这里插入图片描述

    2、模板：

    C++

    #include
#include
using namespace std;
vector<int> mul(vector<int>&A,int&b)
{
    vector<int>C;
    int t=0;
    for(int i=0;i<A.size()||t>0;i++)
    {
        if(i<A.size())t+=A[i]*b;
        C.push_back(t%10);
        t=t/10;
    }
    while(C.size()>1&&C.back()==0)C.pop_back();
    return C;
}
int main()
{
    string a;
    int b;
    cin>>a>>b;
    vector<int>A;
    for(int i=a.size()-1;i>=0;i--)A.push_back(a[i]-'0');
    vector<int>B=mul(A,b);
    for(int i=B.size()-1;i>=0;i--)printf("%d",B[i]);
    return 0;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27

    四、除法

    我们这里说的除法是一个大整数除以一个存储在int类型中的数字。

    1、思路：

    请添加图片描述

    如上图所示，我们创建一个临时的变量t。这个t有两个作用：第一个作用是计算结果的每一位，第二个作用是记录最终的余数。

    2、模板：

    C++

    #include
#include
#include
using namespace std;

vector<int>div(vector<int>&A,int&B,int&t)
{
    t=0;
    vector<int>C;
    for(int i=A.size()-1;i>=0;i--)
    {
        t=t*10+A[i];
        C.push_back(t/B);
        t=t%B;
    }
    reverse(C.begin(),C.end());
    while(C.size()>1&&C.back()==0)C.pop_back();
    return C;
}

int main()
{
    string a;
    vector<int> A;
    int B;
    cin>>a>>B;
    for(int i=a.size()-1;i>=0;i--)A.push_back(a[i]-'0');
    vector<int> C;
    int c;
    C=div(A,B,c);
    for(int i=C.size()-1;i>=0;i--)printf("%d",C[i]);
    puts("");
    cout<<c;
    return 0;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35

    五、总结：

    我们发现上述的模板中都有一个相似的思路：我们都创建了一个临时变量t,这个变量的作用就是来计算每一位，同时去存储进位或者余数。当大家忘记时，自己模拟一下，即可写出上述的模板。希望大家多多研究图片中的例子。

  • 相关阅读:
    Nacos注册中心和服务消费方式（服务治理）
    显示控件——字符显示之数据变量
    宝塔Linux面板命令大全
    JSON（详解）
    深入理解 Python 虚拟机：复数（complex）的实现原理及源码剖析
    2023江西财经大学计算机考研信息汇总
    【山东科技大学OJ】1163 Problem A: 时间：24小时制转12小时制
    【开源】基于Vue.js的生活废品回收系统的设计和实现
    基于JavaSwing开发房产管理系统(access数据库) 课程设计 大作业
    数商云SRM采购管理系统应用流程详解，采购平台助力化工行业提升招标采购质效
  • 原文地址：https://blog.csdn.net/weixin_72060925/article/details/127835289